论文和技术资料

Introduction: Glass relaxation occurs in a range of temperature during transition from equilibrium to super-cooled liquid. Viscoelastic material model can be applied to simulate glass behavior during the glass transition regime and to predict the glass deformation and stress evolution. Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. The generalized viscoelasticity theory involves two kinds of phenomena: stress relaxation and structural relaxation.

Structural relaxation describes the time-dependent change in volume due to the temperature change as well as the thermal history. Stress relaxation involves both viscous and elastic deformation in the dynamic stress-strain response. The dependence of the viscoelastic properties on the temperature can be accounted for by the thermorheologically simple (TRS) assumption, using the shift function concept.

COMSOL Multiphysics® software can simulate the stress relaxation with the WLF (Williams-Landel-Ferry) shift function, but no structural relaxation. In this study we developed a framework of material constitutive model to implement the full viscoelastic model with both structural and stress relaxation in COMSOL. The structural relaxation is captured by the concept of fictive temperature, first proposed by Tool[1]. The fictive temperature can be solved by a differential equation. We can also use different shift functions in addition to the WLF shift function. A shift function widely used in glass simulation is the one proposed by Narayanaswamy[2], which considers the influence of fictive temperature.

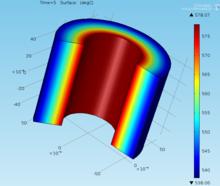
Use of COMSOL Multiphysics: COMSOL software is used to solve the stress evolution when a glass tube cools from above glass transition temperature to below glass transition temperature, shown in Figure 1. Since the inner surface and outer surface are cooled with different rates as shown in Figure 2, thermal stress is induced due to the thermal expansion mismatch. A 2D axisymmetric solid mechanics module is set up for simulating the problem. A domain ODE is added for both the fictive temperature variable and thermal strain variable. The thermal strain value calculated then replaces that in the solid mechanics module using the equation view.

Results: For the problem shown in Figure 1, given the thermal loading in Figure 2, the calculated fictive temperature and thermal strain at the center inner surface are shown in Figure 3 and compare well with other commercially-available simulation software. The axial and hoop stresses at the center inner surface are shown in Figure 4. They are also close to the other software results.

Conclusion: In this study we developed a framework of material constitutive model to implement the full viscoelastic model with both structural and stress relaxation in COMSOL software. The fictive temperature and thermal strain are solved by added domain ODEs. Any type of shift function can be implemented. Particularly the Tool-Narayanaswamy shift function is implemented in this work, to include the fictive temperature dependence in the shift function. Viscoelastic stress is solved efficiently with the COMSOL model and the results compare well with the other software results.