论文和技术资料

In recent years, conventional rigid and planar sensor devices are gradually substituted by flexible and stretchable alternatives. This paradigm shift has paved the way to entirely new applications, particularly in the field of personalized health monitoring or environmental sensing. Despite latest developments towards novel (additive) fabrication techniques and enhanced functional materials, it remains a major challenge to design flexible and shape-adjustable sensors with an excellent durability, sensitivity, biocompatibility and, at the same time, an improved hysteresis behavior. This can be primarily traced back to divergent material properties of hyperelastic substrates like polydimethylsiloxane (PDMS) or thermoplastic polyurethane (TPU) commonly used for stretchable (bio-) sensors in contrast to the antagonistic stress-strain behavior of metals such as copper or silver utilized for embedding conductive and functional traces within the stretchable sensors. Therefore, it is indispensable to study the impact of hyperelastic substrates for next-generation sensor designs and fabrication in depth.

In the present work, numerical investigations of hyperelastic TPU substrates with integrated copper traces serving as resistive and capacitive sensors are presented. TPU is appropriate for various shape-adjustable sensor applications owing to its low elastic modulus and a high bulk modulus, respectively. Nevertheless, strong deformations of TPU sheets are accompanied by geometric nonlinearities which cannot be expressed by a linear stress-strain behavior. Such hyperelastic materials are characterized by an elastic strain energy density function which is defined as a scalar function of the strain deformation tensors. There a several existing hyperelastic material models for description of the relating material behavior of TPU. In a first step, a curve fitting for the Mooney-Rivlin (5-parameter), Ogden (4th order), Neo-Hookean as well as the Yeoh model is implemented based on existing stress-strain measurement data. Due to these findings it could be proven that the 5-parameter Mooney-Rivlin model meets the measurement data of TPU best (cf. Fig. 1). Hence, corresponding material constants of the 5-parameter Mooney-Rivlin model are extracted for a subsequent implementation within the COMSOL sensor models.

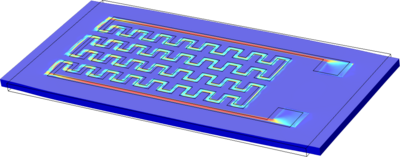
In COMSOL the Solid Mechanics interface is implemented to build up a stretchable resistive sensor or rather strain gauge based on the 5-parameter Mooney-Rivlin model as illustrated in Fig. 2. In this way, considerable strain rates of TPU are achieved without disruption of the copper meanders or delamination of the TPU material. To characterize the resistance behavior of the strain gauge, the Electric Currents interface as well as the Mathematics Module with the Deformed Geometry interface are also utilized within the simulation model. Related to Fig. 3, strain rates for copper meanders up to 60% has shown appropriate simulation results in very good approximation to measurement data. Such high strain rates of conductive traces are also of great importance for lead resistances of stretchable capacitive sensors under dynamic conditions. Hence, a simulation model for a shape-adjustable capacitive sensor is investigated as well, where considerable strain rates up to 40% could also be achieved (cf. Fig. 4). Conclusively, COMSOL constitutes a powerful numerical tool for the predictive analysis of hyperelastic material behavior towards design of next-generation and shape-adjustable sensor devices.