论文和技术资料

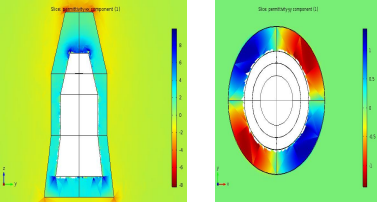
The concept of invisibility in general has been imagined in science-fiction in fascinating ways such as invisible aircrafts, invisible cars, cape of invisibility etc. which has inspired a lot of interest in the field. The first crude attempt at achieving invisibility was inspired from nature, specifically from animal camouflage. It was realized that in order to make something invisible, the electromagnetic (EM) waves had to be controlled in such a way that there remained no signature of the object being cloaked in the outgoing waves. The capacity to make materials whose properties could be tailored at will, lead to the heightened interest in transformation optics. The mathematical formulation was laid out for controlling electromagnetic waves such that they behave in the same way as they would in a deformed space. It involves calculating the permittivity and permeability distribution within an enclosed space around the object. The Jacobian transformation tensor used in transformation optics has an equivalent in the domain of continuum mechanics called the deformation gradient tensor. This has been used as a tool to derive the permittivity and permeability tensors for cloaks and other TO based applications using numerical methods in the past for 2D shapes. In this paper the Laplace’s equation is solved by setting Dirichlet boundary conditions on the inner and outer boundaries of the cloak to get the inverse of the deformation gradient tensor. It is then used to calculate the final transformation tensor for an arbitrary 3D cloak. Some test case has been studied and are simulated in COMSOL Multiphysics software. MATLAB has been used to solve the final Jacobian matrix, and the final permittivity and permeability tensor are found and are used in COMSOL Multiphysics as the input in the materials property node for the cloaked region.