学习中心

Tracking Eigenmodes in Parameter Sweeps

---

When performing an eigenfrequency analysis in conjunction with a parameter sweep, the mode solutions may not always be ordered by mode family. This becomes particularly evident when there are mode crossings or degeneracies in the linear system. Here, you will learn how to categorize eigenmodes using the mode overlap integral in COMSOL Multiphysics^®.

A Simple Example

Let's consider a relatively simple example: the 2D wave equation on an elliptical domain with fixed external boundaries (displacement). We solve for the first five eigenmodes while sweeping the height of the ellipse. The width of the ellipse is fixed at, while the heightvaries between 8 cm and 12 cm. In the middle of the parameter range, the simulation domain is a perfect circle, and the symmetry causes some eigenmodes to be mutually degenerate. The magnitude of displacement for each of the first five modes can be seen below.

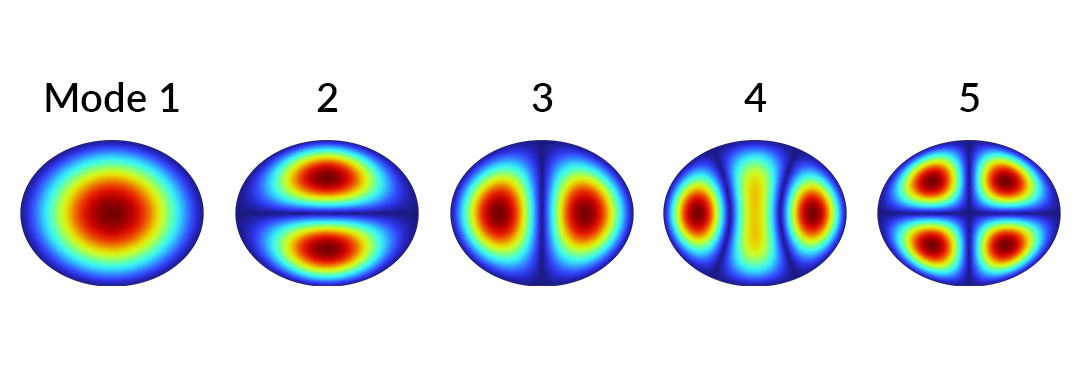
The first five eigenmodes while sweeping the height of an ellipse.

Note the mode crossing atwhen the natural frequencies are plotted against height.

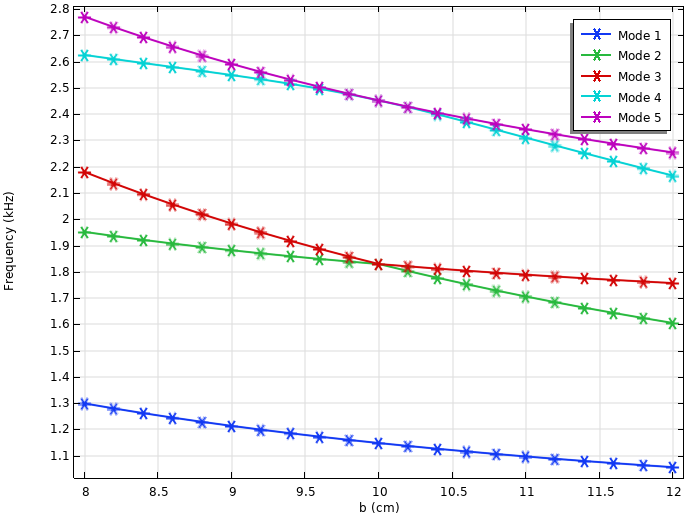
Eigenfrequencies of the 2D wave equation plotted against the height of the elliptical domain. Note the mode crossing at b = 10 cm.

Upon closer inspection, we find that modes 2 and 3 are mixed up post-crossing. This happens because the eigenvalues are colored according to their order in the solution dataset. To remedy this, we can use the mode overlap integral to categorize the mode solutions:

The equation above is defined in the most general sense, withandrepresenting two arbitrary eigenmode solutions. The integrals are performed over the entire simulation domain, and the star suffix indicates complex conjugation. The numerator represents an inner product between the two modes, whereas the denominator normalizes the value ofto lie between 0 and 1. For this specific problem, the overlap integral can be simplified to

In the following sections, we will demonstrate how to implement the overlap integral calculation to categorize modes. You can follow along by opening the starting model filehere.

Defining a Mode Normalization Variable

The first step is to define a mode normalization variable so that it can be referenced later in the overlap integral calculation. The mode norm is mathematically defined as follows:

First, create an integration operator that covers the entire simulation domain.

Settings window forIntegrationnode.

Next, create aVariablesnode and define amodeNormvariable that uses the following expression:

intop1(u^2)

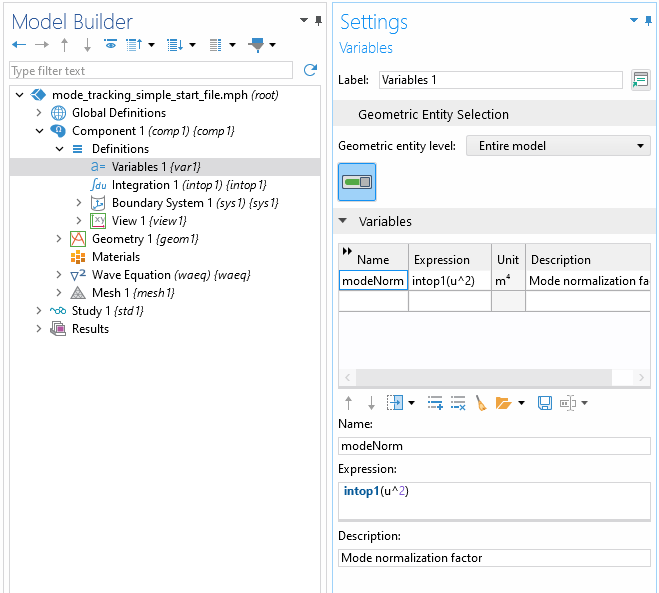
Settings window for Variables node.

Note that the appropriate expression will differ depending on the model physics and dependent variables. For instance, when the dependent variables are components of the electric field, then the integrand should define a dot product of the field with its conjugate.

After defining themodeNormvariable, compute the study.

Using the Join Dataset to Set Reference Modes

We will use theJoindataset to facilitate comparison between a particular mode solution (also known as the reference mode) and the complete mode solutions. The reference mode should be a solution that is representative of the tracked mode family.

After computing the study, right-click onDatasetsand selectJoin.

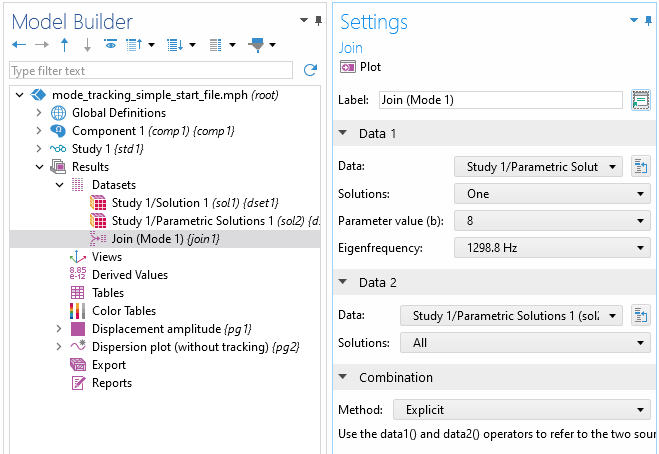
Settings window forJoinnode.

SetData 1to point to the reference mode. In this case, we select the first eigenmode for the case. SetData 2to point to the complete solution. For the combination method, chooseExplicit.The explicit method allows us to reference specific variables in each solution using thedata1()anddata2()operators.

Calculating the Mode Overlap Using an Evaluation Group

Next, right-click onResultsand add anEvaluation Group.Set the source dataset to theJoindataset.

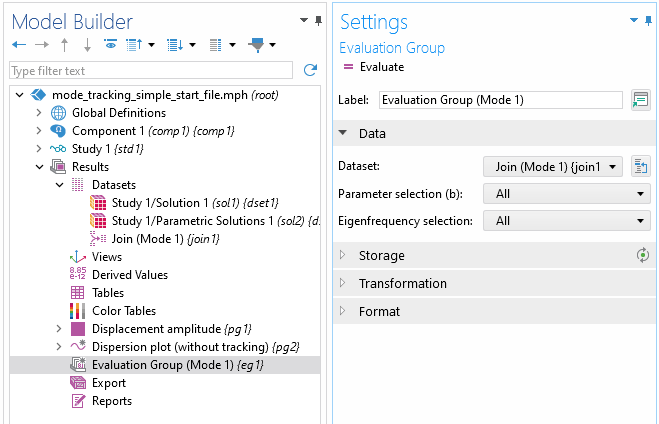
Settings window forEvaluation Groupnode.

Right-click on the newEvaluation Groupnode to add aSurface Integrationsubnode. (For 3D problems, replaceSurface IntegrationwithVolume Integration.) For selection, selectAll domains.The expression to be integrated is as follows:

data1(u)*data2(u)/sqrt(data1(modeNorm)*data2(modeNorm))

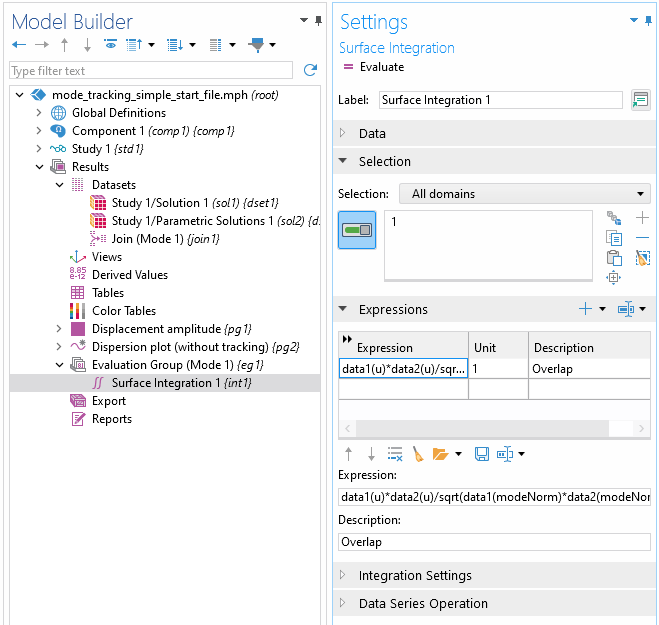
Settings window forSurface Integrationsubnode.

Here,data1(u)refers to the displacement of the reference mode, anddata2(u)refers to the displacement of the other modes. In the denominator, we reference the mode normalization variable that we defined earlier.

Next, modify theTransformationsettings in theEvaluation Groupnode settings, as shown in the following screenshot.

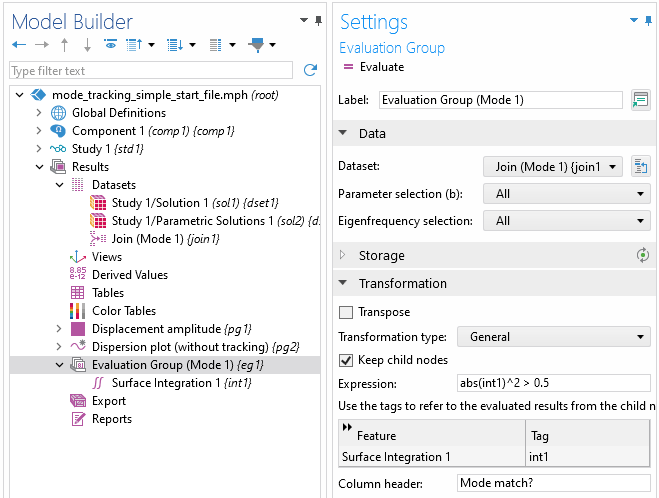
Settings window forEvaluation GroupnodeTransformationsettings.

In the expression box,int1refers the integral value calculated by theSurface Integrationnode, andabs(int1)^2gives the value ofas defined in equation 2. The intention here is to generate a new Boolean data column which indicates whether the overlap value is a match for the reference mode (1 is a match, 0 is not). Hence, there is a logical comparison betweenand a threshold value of 0.5 in the expression.

Note that the threshold value is not fixed, but instead may vary from problem to problem or between different mode families. The goal is to pick a threshold value that cleanly separates solutions belonging to the desired mode family from the rest. In problems where there is a wide spread of mode overlap values, some fine-tuning via trial and error may be necessary.

In theColumn headerbox, shown in the screenshot above, we can optionally give a title to this transformed data column. We can also check theKeep child nodesoption to preserve the original overlap data column. When you are done, click theEvaluatebutton. Be aware that the calculation may take some time, especially for large models.

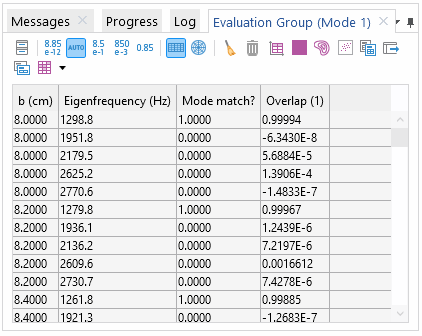
Table forEvaluation Group.

After evaluating, a table should display that looks similar to the above. If you wish to add more data columns the table, you may do so by adding additional evaluation nodes to theEvaluation Group.Remember to use thedata1()anddata2()operators to reference the appropriate mode solution.

Plotting with Table Graph

Create a1D Plot Groupand add aTable Graphnode.

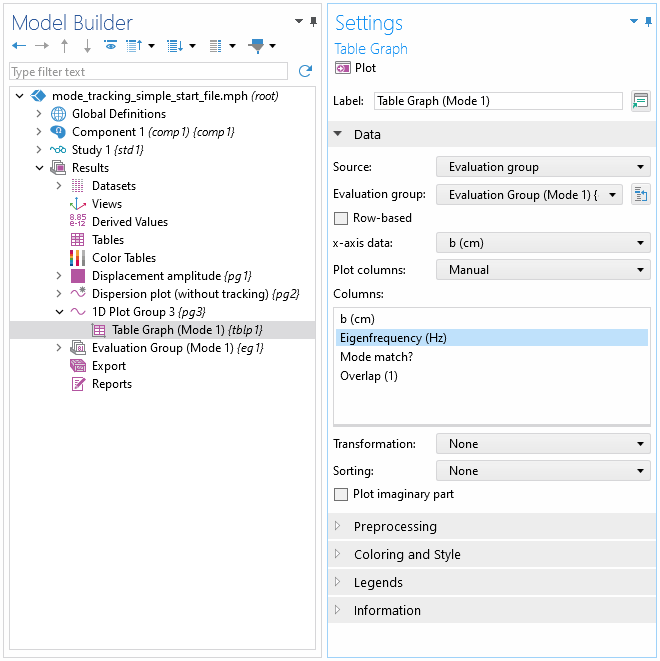
Settings window forTable Graphnode.

For source, pick the newly createdEvaluation Group.Select the appropriate x-axis data (swept parameter) and plot column (eigenvalue). Feel free to adjust the coloring, style, and legend options as desired.

Next, right-click on theTable Graphnode and add aFiltersubnode. In the expression box, entercol3==1. Here,col3refers to the mode match data column.

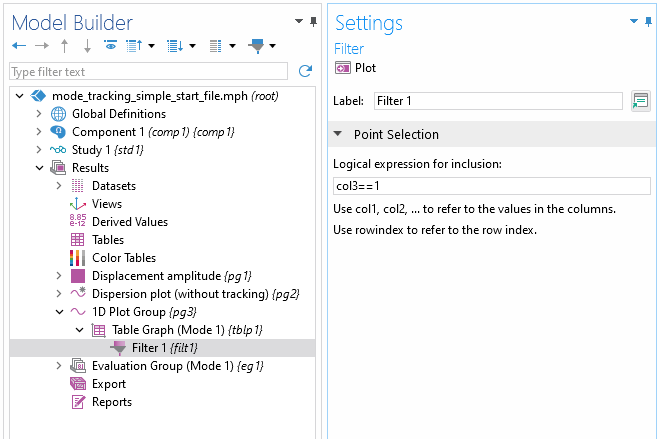
Settings window forFiltersubnode.

TheFiltersubnode filters the plot data based on a given logical criteria. In this case, only the matched mode solutions are plotted. Click thePlotbutton to execute the plot.

Tracking Additional Mode Families

To track additional mode families, we simply repeat the previous steps. You can make use of theDuplicateaction to quickly set up additionalJoin,Evaluation Group, andTable Graphnodes. To do so, right-click on the respective node and selectDuplicate(CTRL-SHIFT-D shortcut). For each new mode family:

1. Duplicate theJoindataset. Rename the node and update the Data 1 section to point to a new reference mode.
2. Duplicate theEvaluation Group. Rename the node and change the source dataset to the newJoindataset. ClickEvaluateto obtain the data table.
3. Duplicate theTable Graphnode. Change the evaluation group source to the new evaluation group. Change color, style, and legend options as desired. ClickPlotto update the plot.

You can also group nodes together to better organize the model tree. To do so, highlight all the nodes to be grouped, right-click and selectGroup(CTRL-G shortcut).

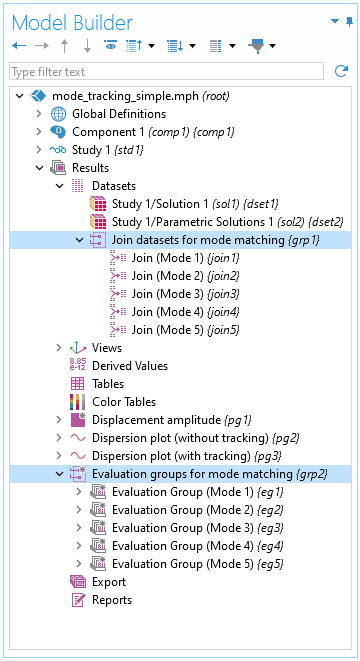
Model Builder tree showing groups for mode matching.

Important Usage Notes

• Remember to reevaluate eachEvaluation Groupafter making any changes that would affect the mode match result.
• After clearing solutions or making significant changes to the eigenfrequency study, it is sometimes necessary to set up the reference modes in theJoindataset(s) again. For better reproducibility, we recommend keeping track of the reference mode used for eachJoindataset in an external document.
• Regarding the choice of reference mode, we recommend choosing a mode that overlaps well with the rest of the modes in its family, while having little resemblance to the remaining modes. Usually this can be determined visually by plotting the mode solutions. If a mode family evolves significantly over the parameter range, some trial and error may be needed to find the appropriate reference mode.

Further Learning

Check out thisblog postfor a demonstration of mode tracking applied to various physics applications. To learn more about theJoindataset and its various other uses, see thisblog post.