多物理场拓扑优化的实现

来自 Jabra 的特邀博主 Junghwan Kook 介绍了一个多物理场拓扑优化框架，以及它的优势，并演示了如何使用它。Junghwan Kook 是参考文献 1 的论文作者，其论文中的一些插图被用在了这篇博客中。

这篇博客介绍了一个使用 COMSOL API 接口和 LiveLink™forMATLAB^®构建的多物理场拓扑优化框架，此内容已在参考文献 1 上发表。文中通过一个可以使用 COMSOL Desktop^®解决的声-结构相互作用 (ASI) 问题对该框架进行了演示。这个框架的优势是它能够解决（当前）与 COMSOL Desktop^®不兼容的问题。

动机

拓扑优化问题总是使用基于梯度方法来求解，这需要使用伴随灵敏度分析。如果基础方程是稳态的或瞬态的，COMSOL Desktop^®支持求解此类问题。因此，最常见的问题，包括频域问题，都可以解决。对于上述框架，它在某些情况下提供了一些独特的优势。例如，它能够：

• 将目标或约束与稳态和瞬态求解器相结合
• 测试自定义优化求解器
• 支持灵敏度不一致的情况，可使用包括灵敏度过滤或类似的启发方式
• 在不重新初始化优化求解器的情况下，更改迭代之间的数值参数的值

虽然这些优势可能与学术研究用户最相关，但也有一些优势会吸引所有用户。例如，该框架可以在以下情况下避免冗余计算：

• 对于扫描问题（例如多个载荷工况），可以避免计算所有扫描参数值的约束灵敏度
• 对于扫描参数仅影响某些因变量的情况，可以将解限制为除扫描参数的第一个值之外的所有变量

在迭代求解器的背景下，避免一些冗余计算工作可能不太重要，并且上述框架其实增加了计算和工程时间。尽管如此，该框架确实有可能加快上述列出情况的计算速度。

拓扑优化

COMSOL Multiphysics^®软件的功能强大，我们可以利用 LiveLink^™forMATLAB^®的功能实现拓扑优化框架，同时利用 MATLAB^®编程环境的易用性和快速实现的优势。

拓扑优化是一种有效的方法，在满足产品性能目标的同时，针对给定的载荷和边界条件，可以在给定的设计空间内优化材料分布。在早期概念设计阶段使用拓扑优化方法，可以取代昂贵且繁琐的设计迭代，以达到最佳设计效果，从而节省时间。尽管在过去几十年里，拓扑优化不断发展并被广泛采用，将拓扑优化应用于新的应用领域（即将拓扑优化与现有软件包不支持的物理过程相结合）仍然具有挑战性。下面列出了开发多物理场拓扑优化算法或程序的几个难点。

1. 为多物理场问题开发有限元模型
2. 材料插值和设计变量的参数化
3. 目标函数和设计灵敏度分析
4. 后处理和操作拓扑设计结果

上述列出的挑战通常会使普通从业者和研究人员不愿将自己已经发表的一些教学案例和简单框架扩展到多物理场拓扑优化。

这里讨论的拓扑优化算法和程序是使用 COMSOL API 和 LiveLink^™forMATLAB^®开发的，适合那些希望在多物理场问题中使用拓扑优化设计的用户。

多物理场问题有限元模型的发展

我们可以通过 COMSOL API使用模型对象访问和轻松操作 COMSOL^®模型的所有特征和数据结构，它提供了多种方法让用户可以执行任务，例如创建几何和网格，以及设置和运行操作序列来求解模型。模型对象的结构符合 Java^®编程语言环境，并提供了几种方法来执行有限元分析和优化所需的一系列任务。我们可以使用 LiveLink^™forMATLAB^®来访问模型对象和实用函数。

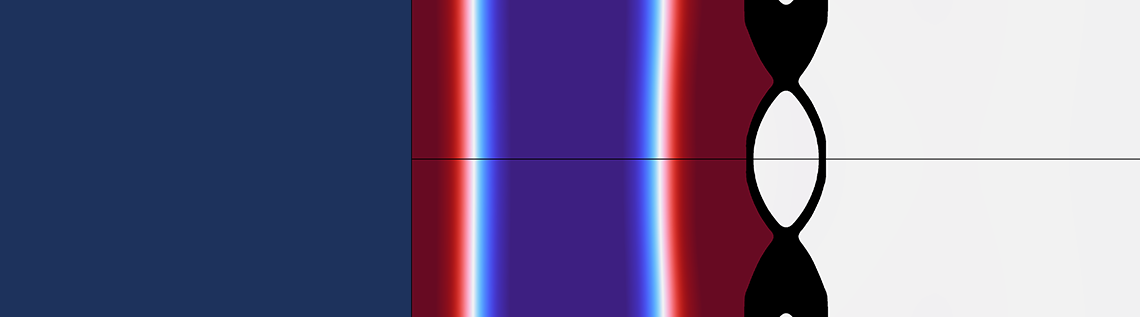
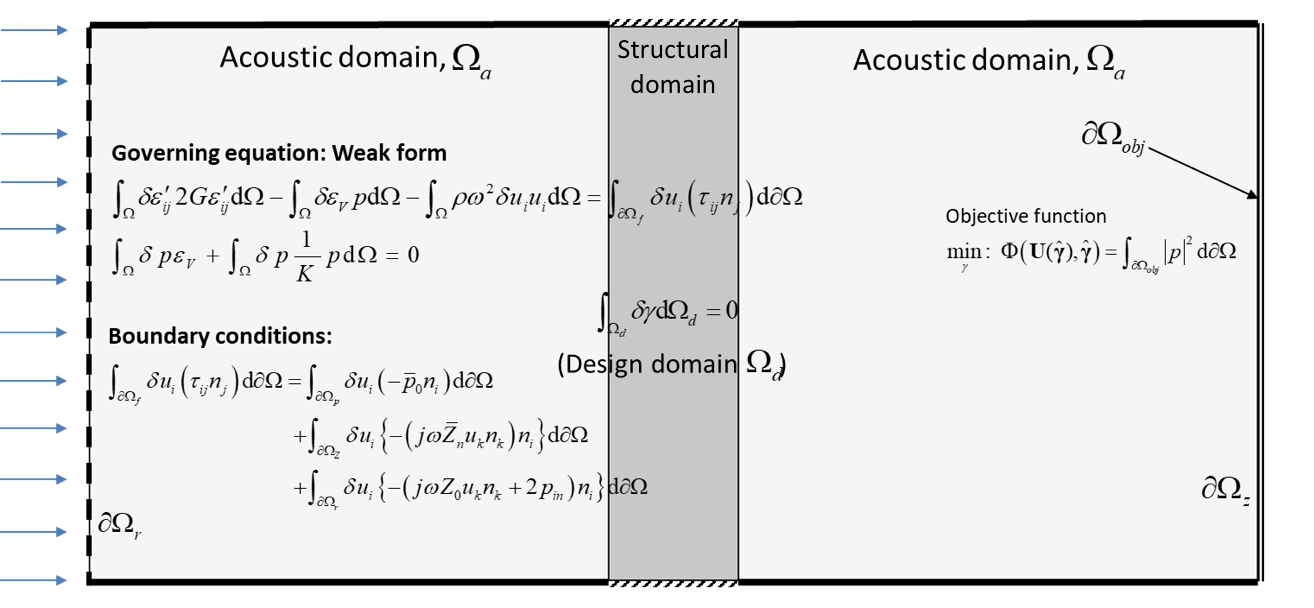
采用 ASI 问题的拓扑优化来证明所引入的框架在系统设计多物理场问题方面的有效性（参考文献 1）。两个声域之间的分区结构的设计问题如图 1 所示，该问题被用作求解多个 ASI 拓扑优化的基准问题。我们可以使用拓扑优化来设计分区结构，以使从入口辐射的声压在出口处最小化。

图1. 考虑声-结构相互作用的基准拓扑优化问题的示意图。

在示例中，将位移(\textbf{u})和压力(p)作为状态变量 (a 公式\textbf{u}/p）的混合有限元公式，用于解决 ASI 问题的拓扑优化问题。我们可以对所有结构、声学和完全耦合的 ASI 问题进行模拟，而无需通过更改混合的公式\textbf
{u}/p中的材料属性，来明确构建声学和结构域之间的边界条件。因此，对于结构-声学相互作用问题，公式\textbf{u}/p有助于实现基于密度的拓扑优化。

COMSOL^®支持混合有限元公式，但该框架不限于软件的物理场接口，因为它还包括来自 MATLAB^®编程环境的基于方程的仿真功能。例如，如图 2 所示，图 1 中位移场的域积分项扩展为直观的弱形式（见公式 (A)），我们可以通过弱形式偏微分方程接口，使用 COMSOL 可解释的语法轻松实现该公式，即

-((test(ux)-test(vy))*G*(ux-vy)+(test(uy)+test(vx))*G*(uy+vx))

+(test(ux)*p+test(vy)*p)+rho*omega^2*(test(u)*u+test(v)*rho*v.

有关在 COMSOL API 中实现弱形式的更多详细信息，请查阅参考文献 2 和 3。此外，我们还可以通过查看图 3 中显示的代码来获得一些灵感，这些代码指示了拓扑优化框架的基本步骤。例如，图 2 中的方程(A)、方程(B)和方程(C)可以使用图 3 所示的模型对象和方法来实现。

图2. 使用混合的\textbf{u}/p公式的声-结构相互作用问题弱形式方程，和用于拓扑优化问题所需的一些基本任务。有限元系统方程包括设计变量和状态变量，例如方程(E)；目标函数和约束，例如方程（F）;和设计灵敏度分析，例如公式(G)。

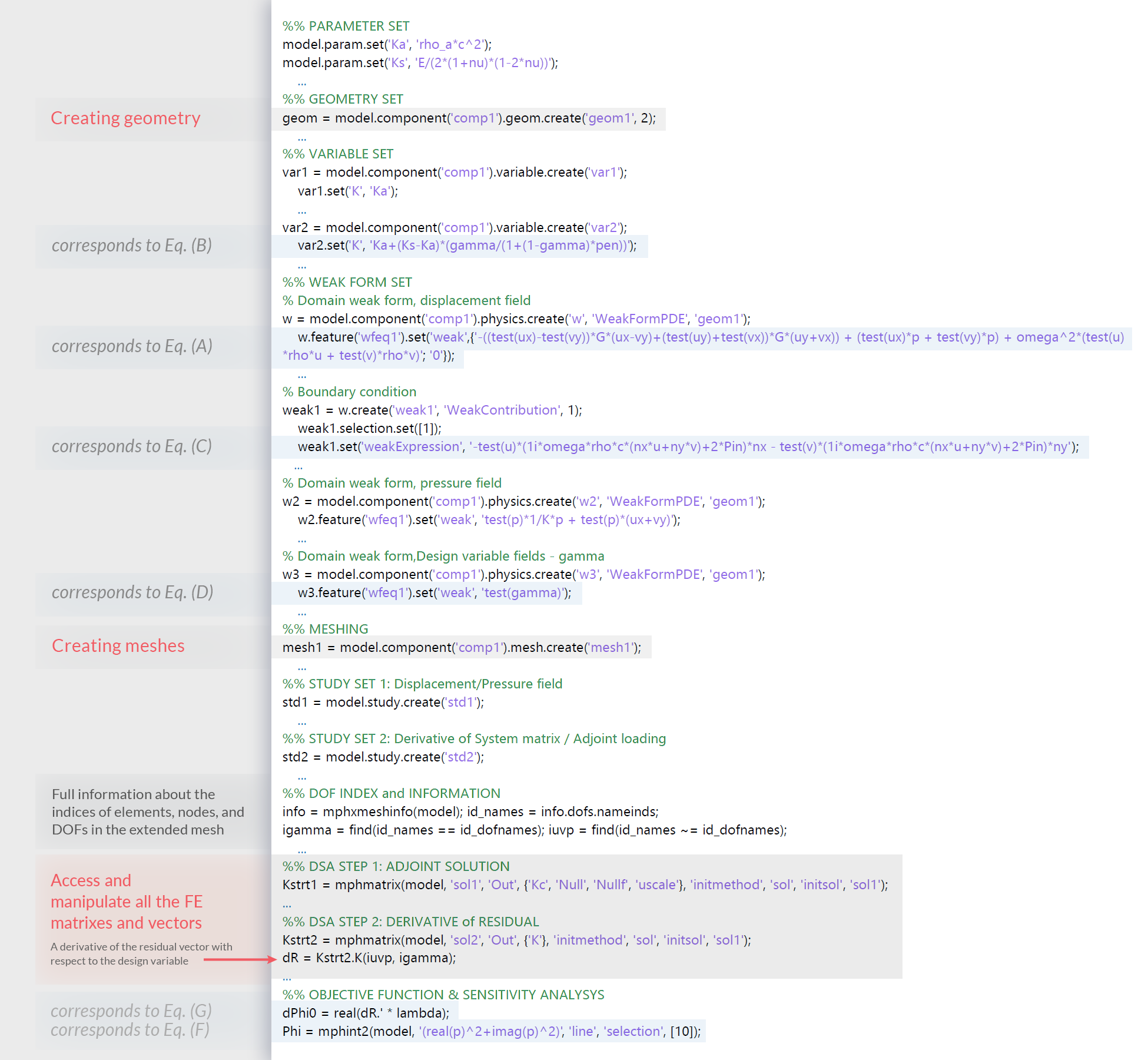
图3. 为拓扑优化过程所需任务选择的 COMSOL API 和 MATLAB^®代码。COMSOL API 语法可以轻松方便地处理所需的任务，无需多行复杂的代码。

设计变量的材料插值和参数化

拓扑优化最终会在设计域中找到一种材料和另一种材料(或空隙)的最佳分布，用于优化目标函数。在 ASI 问题的优化过程中，通过密度\rho、体积模量K和剪切模量G取与空气和固体材料对应的两个极值之间的值，以得到优化的设计。这些值由具有设计变量场\gamma的材料插值函数引入，如图 2 中的方程(B)所示。

式中，p_K和p_G是可以控制设计变量场的中间值的参数。使用 COMSOL Multiphysics 中基于方程的仿真，我们可以轻松地将设计变量场作为辅助因变量引入模型中。因此，在设计域中引入了一个额外的控制方程，如图 2 中的方程(D) 所示。在图 3 中看到的代码中，设计域上的域积分项通过设置test(gamma)定义，其中设计变量gamma在弱形式偏微分方程接口中设置为因变量。需要注意的是，设计变量的弱形式偏微分方程接口从未被求解，而仅用于根据优化程序更新设计变量。

COMSOL^®求解器允许我们使用解耦方法解决部分问题，与此同时修复子集。例如，子集方程\textbf{S}_\text{U}\textbf{U}= \textbf{L}_\text{U}可以求解状态变量场，同时将设计变量的值保持在其初始值。设计变量的值在后续迭代步骤中更新。为了访问和更新组装矩阵，我们利用与设计变量和状态变量相对应的自由度(DOF)列表，它是使用mphxmeshinfo函数提取的。这种方法的优点是我们在 MATLAB^®中使用矢量化运算，而不必使用有限元运算，从而提高了代码的可读性和计算性能。由于这种实现方法不依赖于优化器，它可以与任何优化求解器（即任何基于梯度或无梯度的优化器）一起使用。

目标函数和设计灵敏度分析

这里提供的示例中，图2 方程(F)积分形式的目标函数可以使用内置函数mphint2进行计算(参见图 3 所示的代码行)。

伴随变量法(AVM)常用于设计灵敏度分析，因为它在计算涉及大量设计变量的系统的设计灵敏度方面具有很高的效率。我们可以使用mphmatrix函数轻松构建伴随方程和导数，该函数会提取所需的矩阵和向量并以 MATLAB^®结构格式将它们返回。特别是，在方程(G)中看到的设计灵敏度分析所需的导数项，可以通过指定状态和设计变量的索引直接从组合矩阵中提取，因为设计变量场被视为组合矩阵中的状态变量之一。设计灵敏度分析可以应用于其他问题而无需进行实质性修改。

对生成的拓扑设计进行后处理和操作

LiveLink^™forMATLAB^®提供了一种可访问的可视化方法，可以对每次优化迭代的优化分析结果，以及所开发程序的整体操作生成清晰的视图，用于排除和修复优化过程中可能出现的问题。图 4 显示了每次迭代的拓扑设计以及目标函数和体积分数的迭代历史，这些在 MATLAB^®环境中都可以看见。

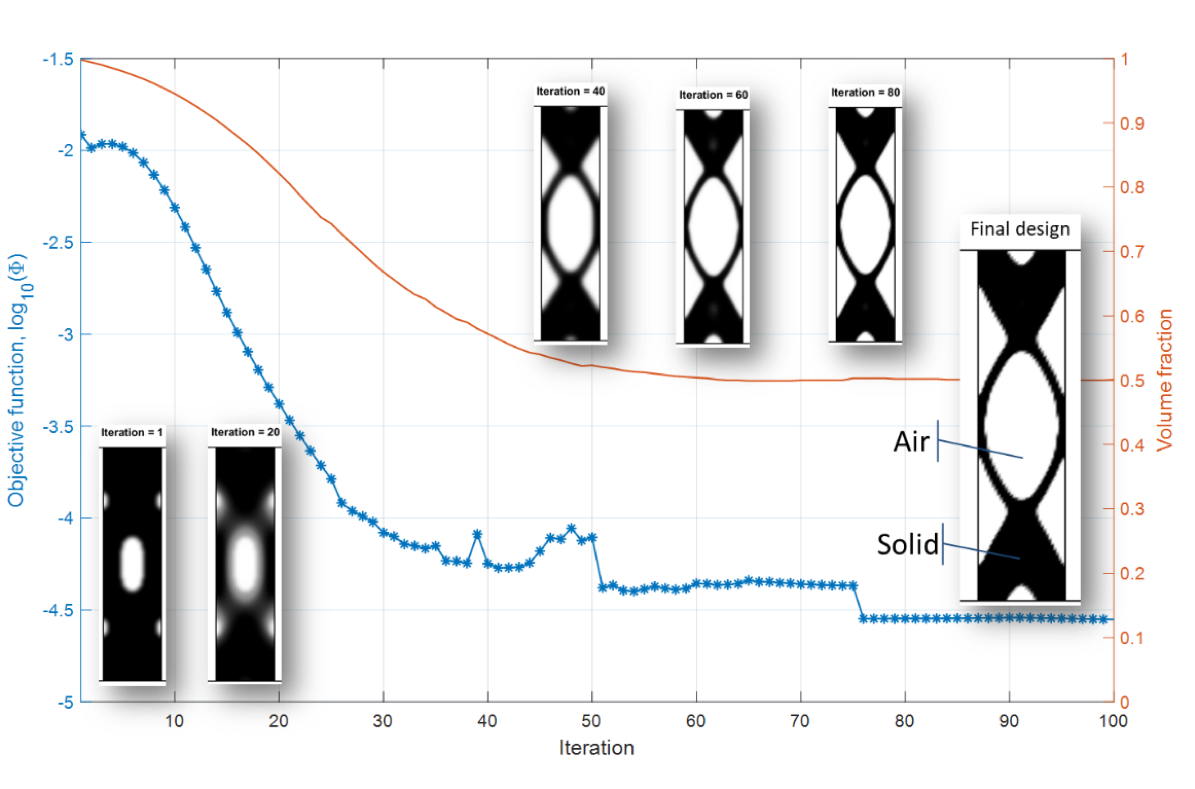
图4.每次迭代的拓扑设计（参考文献1）以及目标函数和体积分数的迭代历史都在MATLAB^®环境中可以看见。

在仿真软件中求解多物理场问题，需要从拓扑解中获得各种绘图，来解释优化设计。我们可以将在 LiveLink™ for MATLAB^®环境中开发的最终模型保存在一个 MPH-文件中，该文件包含 COMSOL^®模型对象，包括所有方法和数据结构。保存的解可以在 COMSOL Desktop^®环境中打开，以便在设计工作流程中对产生的拓扑结构进行后处理和操作。然后，我们可以使用模型开发器窗口轻松创建不同的拓扑结果绘图。如图 5 所示，通过使用滤后处理过滤功能，得到了固体和空气之间有明显边界的最终设计。为了显示性能，生成了一个变形结构来说明优化后拓扑设计的受力变形情况。

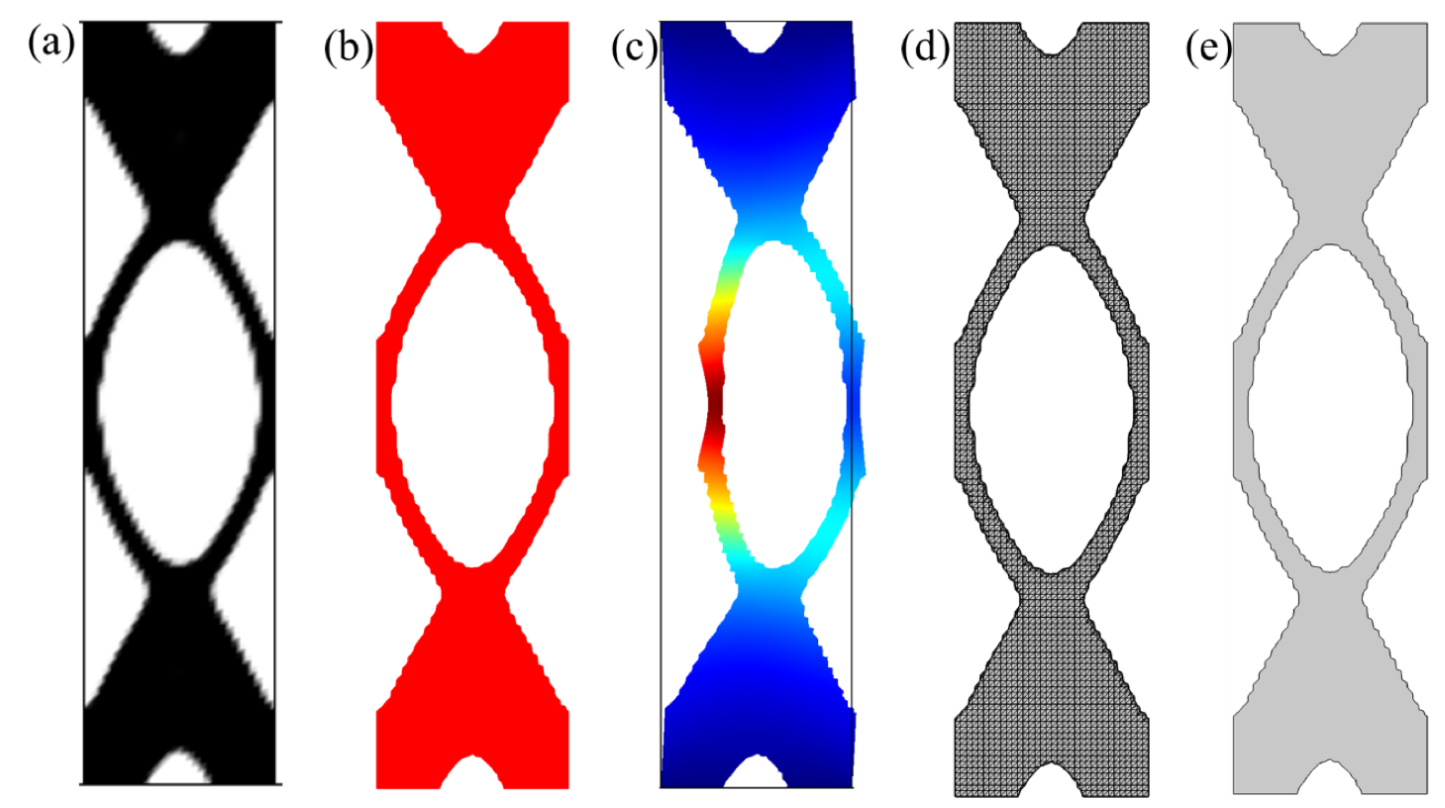
图5. (a)优化后获得的最终设计。(b)使用阈值过滤得到的具有清晰耦合边界的拓扑。(c)具有位移幅值场的变形结构。(d)导入的网格零件。(e)用于 3D 打印和增材制造的导入网格零件创建的 2D 几何图形。所有图均来自参考文献 1.

优化的设计可以导出为 CAD 模型，用于进一步分析和原型制作。将数据集导入 COMSOL Desktop^®后，我们可以使用优化结果创建网格文件和 CAD 文件。几何对象可用于进一步分析，也可导出用于 3D 打印。

使用 COMSOL Desktop^®重现拓扑优化问题

这篇博客深入探讨了使用 COMSOL API 和 LiveLink™forMATLAB^®进行多物理场拓扑优化，并概述了其他相关的主题，包括有限元和设计灵敏度分析以及后处理。COMSOL API 和 LiveLink ™forMATLAB^®使初学者能够使用最少的编程实现高级拓扑优化。由于设计变量场的离散化和灵敏度分析方法不限于特定问题，因此本博客中涵盖的通用框架，能够解决其他类型的拓扑优化问题，而无需大量修改。此外，引入的框架提供了与高级语言相同的开发自由，这并不限制我们研究需要访问优化参数以及数值计算中的一些矩阵和向量的新拓扑优化技术和方法。它还提供了一种有效的方法来解决和修复优化过程中可能出现的问题。

注意：要获得使用 LiveLink^™forMATLAB^®进行优化的详细描述和代码，请查看参考文献 1。

此外，COMSOL Multiphysics 提供了对用户友好的优化模块插件，使我们能够通过其多物理场和用户定义的偏微分方程求解器来求解拓扑优化问题。使用 COMSOL Desktop^®进行拓扑优化，我们可以仅使用内置功能重现相同的多物理场拓扑优化问题(见图 6)。该模型使用固体力学(用于优化域)的混合公式选项和压力声学(用于纯声学域)，并结合了优化模块中的最新优化方法和过滤方案。

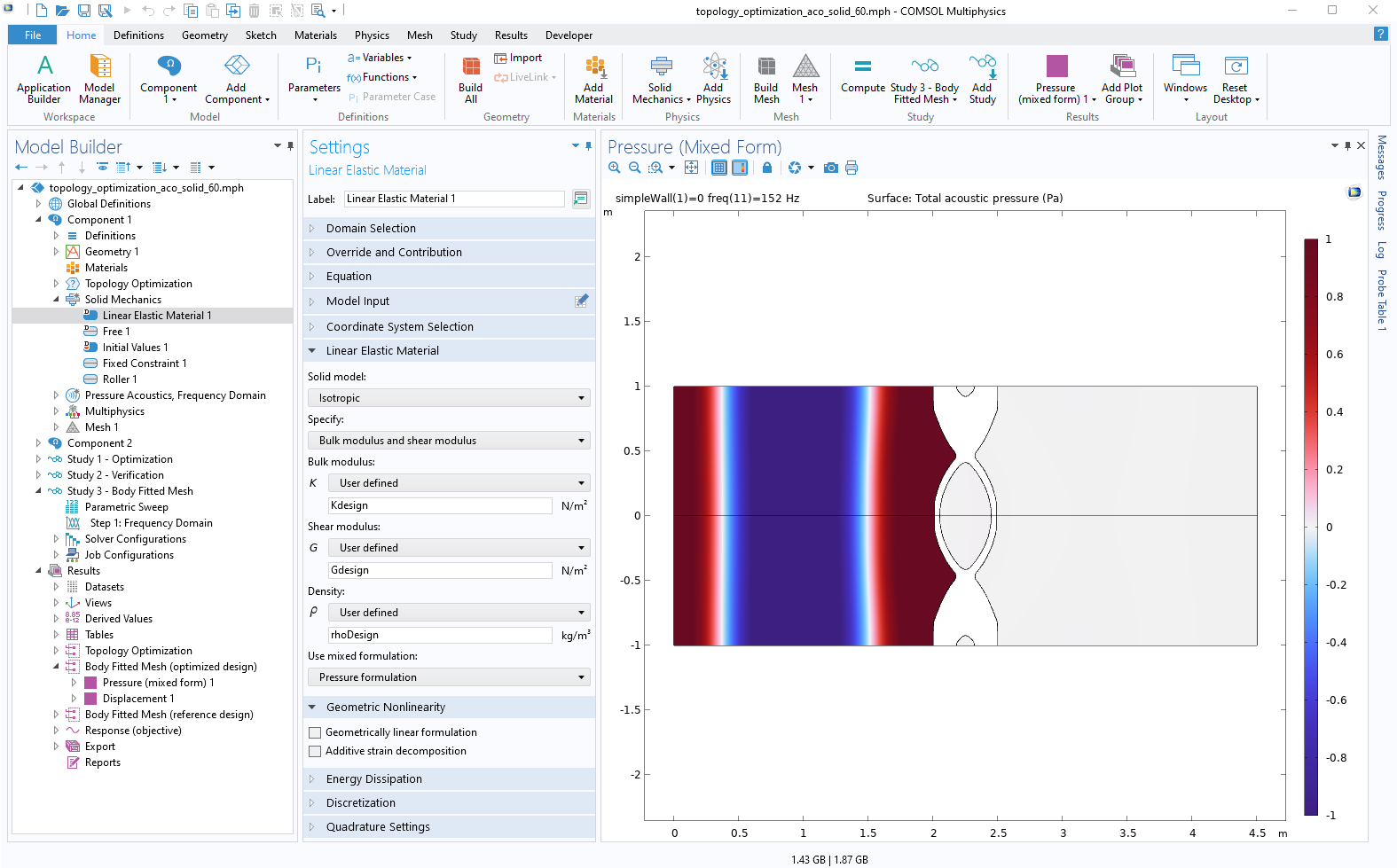
图6.仅使用内置COMSOL Desktop®功能重现相同的多物理场拓扑优化问题。

您可以单击下面的按钮，进入 COMSOL 案例库查看图 6 所示的模型。

关于作者

Junghwan Kook (JK)于 2012 年在韩国光州科技大学（Gwangju Institute of Science and Technology）信息与机电一体化学院获得博士学位。之后，他在丹麦技术大学 (DTU) 机械工程系从事博士后研究。2015—2017 年，任 DTU 电气工程系声微机械系统研究中心助理教授。2017 年至今，他一直在 GN Audio A/S 公司从事科研工作，也就是 Jabra，该公司是工程通信和声音解决方案领域的领先品牌，通过创新为消费者和企业提供支持。他目前的研究兴趣包括多学科设计优化、声学和机械设计的数值方法、声音质量、以及声学和振动声学特性的实验分析。JK 一直使用 COMSOL Multiphysics 建模与仿真真实世界的多物理场系统，为用户提供高质量的解决方案。

参考文献

1. J. Kook and J.H. Chang, “A high-level programming language implementation of topology optimization applied to the acoustic-structure interaction problem,”Structural and Multidisciplinary Optimization, vol. 64, pp. 4387–4408, 2021.
2. C. Liu, “Implementing the Weak Form in COMSOL Multiphysics,” COMSOL Blog, 2015;//www.denkrieger.com/blogs/implementing-the-weak-form-in-comsol-multiphysics
3. C. Liu, “Implementing the Weak Form with a COMSOL App,” COMSOL Blog, 2015;//www.denkrieger.com/blogs/implementing-the-weak-form-with-a-comsol-app

MATLAB is a registered trademark of The MathWorks, Inc. Oracle and Java are registered trademarks of Oracle and/or its affiliates.