
在结构工程中,屈曲不稳定性是一种危险的现象,载荷的微小增加就可能会导致灾难性的破坏。这篇文章我们将研究一些屈曲问题以及如何分析它们。
什么是屈曲?
你有没有见过一个成年人可以在一个空的易拉罐上保持平衡的游戏?
尽管易拉罐的内壁只有 0.1mm 厚,但只要保持完整的圆柱形状态,就可以承受一个成年人的重量。此时,轴向应力低于屈服应力,这可以通过力除以横截面积来验证。

如果你只是轻轻地按压圆柱形表面上的某个点,易拉罐就会塌陷。完整圆柱体的极限载荷高于人的重量,但是一个轻微的变形就能明显降低它的承载能力,这种现象称为缺陷敏感性,是设计压缩结构时可能出现的一个隐患。你可以在这个网页上看到一些坍塌壳的例子,它们的尺寸比汽水罐要大得多。
在数学上,屈曲是一个分岔问题。在一定载荷级别下,解不止一个。下面的草图描绘了解的分岔点和三种不同的可能路径,在分岔点处形成分支。如下图所示,次级路径可以是三种不同的基本类型。
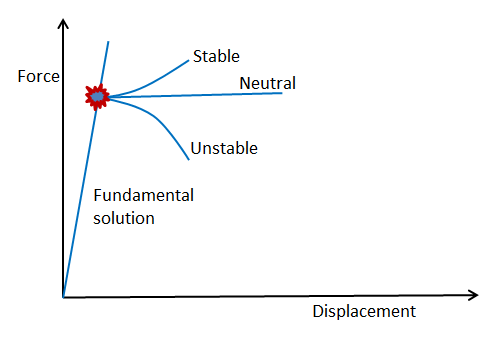
分岔问题的解
如果承载能力继续增加,就可以将解表征为稳定。这是风险最小的情况,但如果你没有意识到这种情况,就可能会计算出太低的压力。因此,你将低估承载能力。中性和不稳定路径更危险,因为一旦达到峰值载荷,位移就可以是峰值点后对应的任意值。
当存在多个解时,就会出现哪一个解是正确的问题。所有的解都将满足平衡方程,但在实际问题中,结构只会选择一种路径,将基于能量最小化来进行这种选择。使用传统线性理论计算的解通常不是首选解。
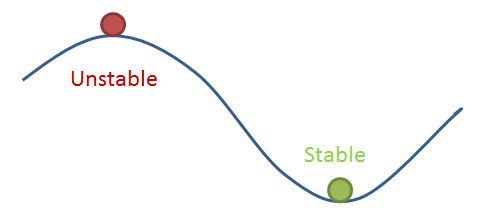
我们可以用波浪形表面上的一个球来做类比,球可以在山顶和山谷中都处于平衡状态,但任何扰动都会使它掉到山谷中。同样,即使是对结构施加最小的扰动也会使它跳到更有利的能量状态。在实际问题中,没有完美的结构;在几何学、材料或载荷方面总会存在扰动。
线性屈曲分析
处理屈曲问题最简单的方法是进行线性屈曲分析。这其实相当于我们在基础工程课程中学过的对简单的结构进行分析的方法。计算压缩支柱的临界载荷(如欧拉屈曲案例)就是这样一个例子。
在 COMSOL Multiphysics 中,有一种特殊的研究类型称为“线性屈曲”。在研究时,需要添加任意大小的外部荷载。它可以是一个单位载荷或预期的工作负荷。这个研究包括两个研究步骤:
- 稳态研究步骤,计算所施加载荷的应力状态。
- 线性屈曲研究步骤。这是一个特征值解,应力状态被用来确定临界荷载因子。
临界载荷因子是需要乘以施加的载荷以达到屈曲载荷的系数。如果使用工作载荷建模,可以将临界载荷因子解释为安全系数。临界载荷因子可以小于 1,在这种情况下,临界载荷比施加的载荷要小。这本身并不是一个问题,因为分析是线性的。临界载荷因子甚至可以是负的,在这种情况下,屈曲所需的最低载荷的作用方向与施加载荷的方向相反。
特征值的求解也会提供屈曲模式的振型。请注意,模式的振型只在一个任意的比例因子内已知,就像特征频率分析中的特征模式一样。
在详细介绍之前,必须提出一些注意事项:
- 对于一些结构,由于缺陷敏感性,使用这种方法获得的理论屈曲荷载可能明显高于实际遇到的载荷。这对于薄壳尤其重要。
- 有些结构甚至在屈曲之前就表现出明显的非线性。原因可能是结构既是几何非线性又是材料非线性。
- 千万不要在屈曲分析中使用对称条件,即使结构和荷载是对称的,屈曲形状也可能不是对称的。

两个对称框架的屈曲形状,截面略有不同,载荷对称相等。
进行线性屈曲分析时,我们可以将问题看作一个线性特征值问题来求解。屈曲的标准是刚度矩阵是奇异的,因此位移是不确定的。所施加的载荷集被称为\mathbf P_0,而临界载荷状态被称为\mathbf P_c = \lambda \mathbf P_0,其中,\lambda是一个标量乘子。
完全几何非线性问题\mathbf K的总刚度矩阵可以看作是两个贡献的总和。一个是线性问题\mathbf K_L的普通刚度矩阵,另一个是由载荷决定的非线性添加项\mathbf K_{NL}。
在线性近似中,\mathbf K_{NL}与载荷成正比,因此
刚度矩阵在其行列式为零时为奇异矩阵。这个形式是参数\lambda的特征值问题。
{NL}(\mathbf P_0))\mathbf u = \mathbf 0
最低特征值\lambda代表临界荷载因子,相应的特征模态\mathbf u代表屈曲形状。
默认情况下,只计算与最低临界载荷对应的一个屈曲模式。我们可以选择计算任意数量的模式,对于复杂的结构,这可能有一定的意义。可能有几种具有相似临界载荷系数的屈曲模式。由于缺陷敏感性等原因,计算的最低临界模式可能与实际问题中的最低临界模式不一致。
在 COMSOL 软件中,不应将线性屈曲研究步骤标记为几何非线性。给出的非线性项\mathbf K_{NL}是单独添加的。但是,如果确实选择了几何非线性,将解决以下问题:
{NL}(\mathbf P_0))+\lambda \mathbf K_{NL}
(\mathbf P_0))\mathbf u = ( \mathbf K_L+(\lambda +1) \mathbf K_
{NL}(\mathbf P_0))\mathbf u =\mathbf 0
term\lambda+1 中额外的’1’被自动补偿了,所以在两种情况下计算的载荷因子是一样。最好的法则是在预载研究步骤和屈曲研究步骤中都使用相同的几何非线性设置。
你可以在 COMSOL 官网中下载桁架塔的线性屈曲分析模型来研究一个线性屈曲分析示例。
固定载荷和可变载荷
有时,一组载荷\mathbf Q可以被认为是与屈曲分析有关的固定荷载,而另一组荷载\mathbf P_0将与荷载因子\lambda相乘。尽管如此,在计算临界载荷因子时,必须考虑到这两个载荷系统的组合。
在数学上,这个问题可以表述为
(\mathbf Q) + \lambda \mathbf K_{NL}
(\mathbf P_0))\mathbf u = \mathbf 0
在 COMSOL Multiphysics 中,也可以使用以下两种策略中的一种来解决这类问题:
- 将它作为后屈曲分析运行,一组荷载固定,另一组荷载增加。这很简单直接,但从计算的角度来看,这种大规模的计算是不必要的。
- 使用下文介绍的修改后的线性屈曲研究。
由于软件的灵活性,修改内置的线性屈曲研究并不困难,这样它就可以处理这两个独立的载荷系统。要做到这一点,首先要增加一个额外的物理场接口,它只用于计算固定载荷引起的应力状态。仅在稳态分析中求解这个接口,而不在屈曲步骤中求解。
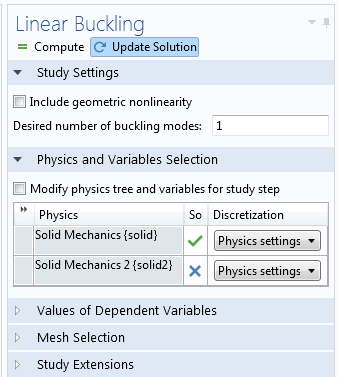
额外的物理场接口在线性屈曲研究步中没有激活。
现在,我们需要根据第二个物理场接口中计算的应力生成屈曲研究中的额外刚度矩阵贡献。可以通过添加以下额外的弱贡献来做到这一点:
{test}(\mathbf E-\boldsymbol \epsilon)
式中,\boldsymbol \sigma^{Q}是来自固定载荷的应力张量,\mathbf E和\boldsymbol \epsilon分别是格林-拉格朗日和线性应变张量。换句话说,差值\mathbf E-\boldsymbol \epsilon包含格林-拉格朗日应变张量的二次项。
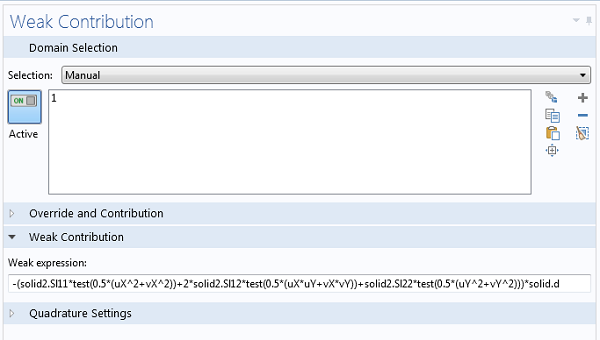
二维固体力学中,来自固定荷载系统的贡献。
现在,我们可以照常运行研究序列,计算出仅适用于第二个荷载系统的临界荷载因子。
后屈曲分析
通过线性屈曲分析,只能找到临界载荷,而不能找到达到临界载荷后发生的情况。在许多情况下,我们只对确保不要达到屈曲的安全临界载荷感兴趣,因此线性研究可能就足够了。
但是,有时需要查看完整的变形历史。造成这种情况的一些原因可能是:
- 该结构在临界载荷之前也具有明显的非线性,因此线性分析并不适用。
- 需要研究缺陷敏感性。
- 有意在部件的后屈曲状态下进行操作。
为了进行后屈曲分析,需要逐步加载结构荷载,并跟踪荷载-挠度历史。在 COMSOL 软件中,你可以使用参数化连续求解器来执行此操作。
进行屈曲后分析并非易事。一个固有的问题是,分叉问题有几种解,如何判断得到的解是预期的呢?此外,在许多情况下,屈曲不稳定性将在数值上表现为病态条件数或奇异刚度矩阵,因此除非使用适当的建模技术,否则求解器将无法收敛。接下来将介绍一些有用的方法。
对称结构
考虑一种简单的情况,例如顶端有一个压缩载荷的悬臂梁。当达到临界载荷时,它可以在三维中沿任意方向偏转,或者在二维中沿两个可能的方向偏转。然而,求解器不太可能收敛到这些解中的任何一个,除非对称性受到干扰,否则对称性问题在屈曲载荷处是奇异的。如果在顶端增加一个小的横向载荷,解就可以顺利地被追踪到。在梁的大变形分析模型中可以找到使用这种技术的例子。
突弹跳变问题
在许多情况下,结构会从一个状态“跳跃”到另一个状态。下面的两杆桁架结构就是一个简单的例子。
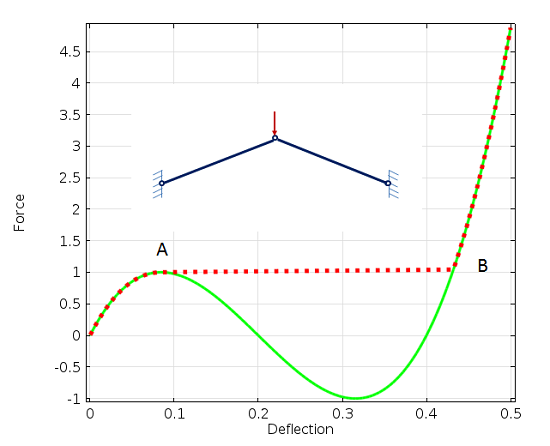
简单桁架结构的突弹跳变分析。挠度为 0.2 时,两个杆是水平的。
当力增加时,它将在状态 A 处达到峰值。从数值上看,刚度矩阵将变得奇异。从物理上看,结构会突然反转并沿着红色虚线跳到状态 B。在实际问题中,这将是一个动态事件。储存的应变能将被释放并转化为动能。
有一个方法可以解决这个问题,就是实际运行一个随时间变化的分析,其中惯性力将平衡外部载荷和内部弹性力。但是,这种方法很少使用,因为它的计算成本很高。
为了追踪绿色实线,可以用指定的位移代替指定的载荷,代替记录反作用力。用指定的位移代替载荷是稳定模型的一个简单方法,但该方法有局限性:
- 它或多或少仅限于外部载荷为单点载荷的情况。
- 指定的位移必须是单调增加。
为了介绍一种更常用的方法,我们以一个浅圆柱形壳体为例,请看下图。它在中心承受单点载荷,因此在这种情况下,你可能很想使用位移控制。但是,如下图所示,在屈曲事件期间,力和它产生的位移都不是单一的。
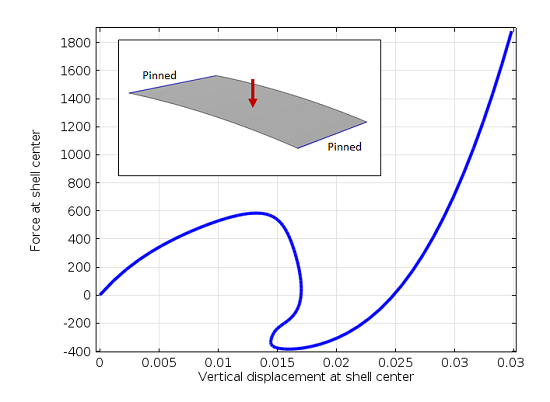
浅圆柱形壳和载荷与位移的关系图。
屈曲事件的动画。
对于这类问题,一些文献会建议你使用弧长求解器。Riks 就是这样一种常用的方法。我们经常被问到为什么不在 COMSOL 软件中添加这样的求解器。答案很简单:我们不需要。
一旦你学会了如何使用 COMSOL Multiphysics 中的连续求解器,像这样的问题是很容易解决的。你只需要在模型中找出一个将单调增加的量,用它来驱动分析。例如,在上面的模型中,可以选择壳体表面的平均垂直位移作为控制参数。
然后,将载荷强度添加为问题中的一个额外自由度,通过全局方程引入。需要满足的等式是平均位移(通过平均算子定义)应等于连续参数(在下面的屏幕截图中调用disp)。
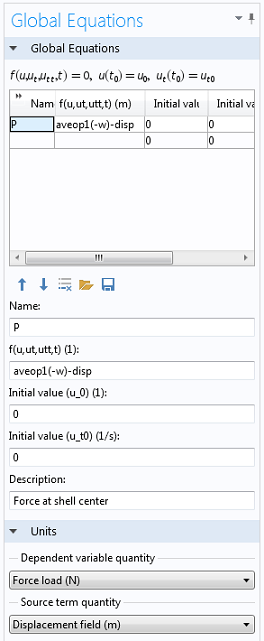
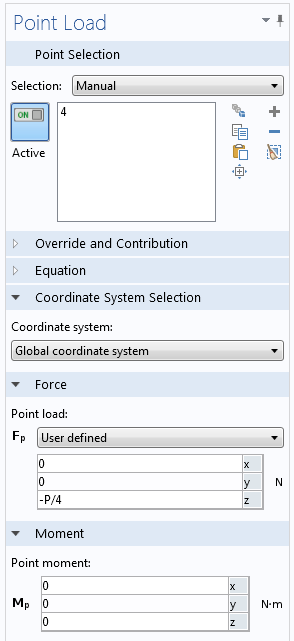
添加一个全局方程来控制载荷。
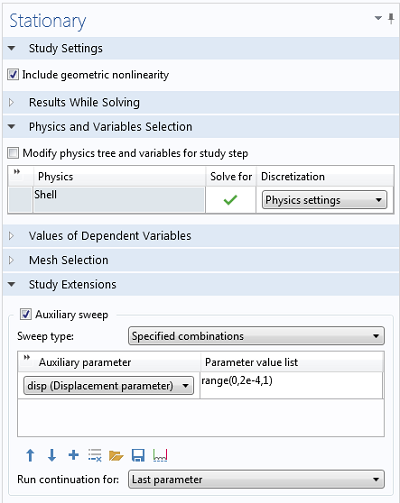
将稳态求解器设置为运行辅助扫描。
您可以从 COMSOL模型库中下载完整的模型。
以上描述的方法不仅适用于力学中的屈曲问题,它还可以求解任何不稳定的问题,例如机电系统的吸合分析。
缺陷
有时,我们需要对缺陷进行显式建模。例如,有一些标准规定,荷载必须具有一定的偏心率,或者梁必须具有一定的假定初始曲率。当引入缺陷时,载荷-挠度曲线将在理想分岔曲线的分支之间走一条“捷径”。
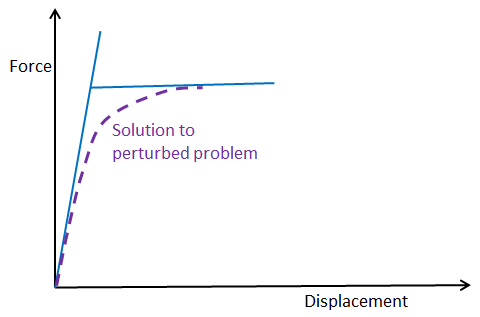
具有初始缺陷的模型的求解路径。
当在一个对缺陷敏感的几何体的模型中加入干扰时,峰值载荷可能会显著下降。这就是前面提到的易拉罐的情况,这是一个物理事实,而不仅仅是有限元建模的效果。因此,对于这类结构来说,最重要的是要真正考虑到缺陷。
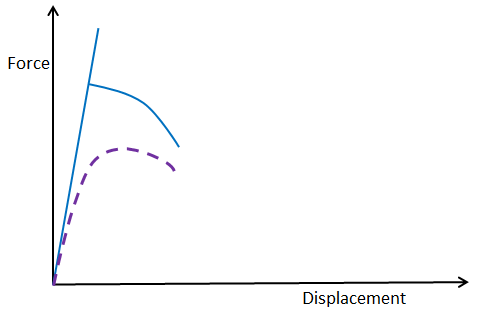
缺陷敏感性模型的求解路径。
那么,应该如何在模型中选择合适的缺陷呢?
我们可以先进行线性屈曲分析,然后将计算出的模式形状作为缺陷。这样做是为了使结构对这种形状最敏感。但是,并不是一定要捕获准确的形状,因此可以使用类似的东西。在考虑制造容差和运行条件时,扰动的大小应与你在实际结构中的预期相似。
在某些情况下,如果临界荷载因子是同一数量级的,那么计算几个屈曲模式并尝试多个模式也是一个好主意。不同屈曲模式之间的缺陷灵敏度差异很大。
使用额外的载荷通常更容易获得扰动,而不是改变几何形状。如果这样做,应确保该载荷所引入的应力不会明显改变问题。



评论 (0)