
在处理随空间变化的导入数据时,我们经常面临的挑战是:确定需要什么级别的网格细化才能准确解析输入数据,以及它将如何影响我们的多物理场问题的解决方案。对于这种情况,我们可以使用 COMSOL®软件的“自适应网格细化”功能,根据模型结果细化网格。事实证明,我们还可以使用自适应网格细化功能,根据输入数据进行细化。下面,让我们了解更多详细内容!
模拟非均匀热负荷
考虑下面显示的问题,一块材料从上方加热,具有来自外部数据文件的空间变化热负荷,并且具有一些独特但非常不均匀的结构。

从外部数据文件中读取的非均匀外加热负荷的视图。
在 COMSOL Multiphysics®软件中,我们可以简单地使用自适应网格细化来解决问题。COMSOL®软件会根据用户的指定自动细化网格多次,从而提供更准确的问题解决方案。下面绘制了该算法的几次迭代。
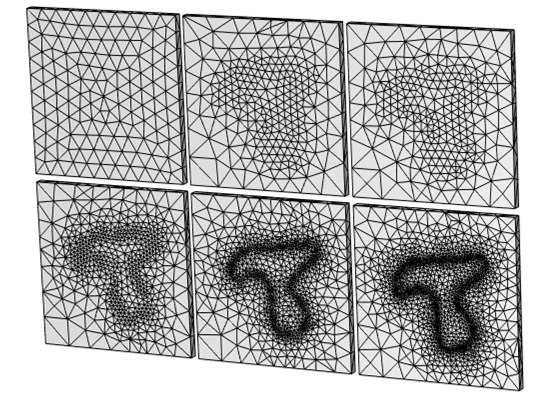
结果显示了使用自适应网格细化时的网格(顶视图)。从均匀的网格开始,COMSOL 软件会调整单元大小,以准确解决由于空间变化所施加的热负荷而导致的解中的变化。这再现了所施加载荷的空间变化,但需要多次迭代才能使这种结构变得明显。
我们可以观察到的是自适应网格细化算法从默认网格开始,它不知道施加的热载荷的形状。只有在多次迭代之后,算法才真正开始很好地识别负载的分布,并且这些初始迭代存在一些计算开销。
如果有更好的方法呢?如果我们可以告诉软件我们想要从一个已经适应实验数据形状的网格开始呢?当然,我们仍然希望执行自适应网格细化,但我们希望从更合理的初始网格开始这个细化过程。
事实证明,通过仅对导入的数据实施亥姆霍兹滤波器(Helmholtz filter)并在其上调整网格就可以了,这很容易做到。我们已经在之前的博文中介绍了亥姆霍兹滤波器的概念和实现以及一些好处。现在让我们看看它的另一种功能。
实现自适应网格细化和数据过滤
我们可以在模型的顶面上实现一个亥姆霍兹滤波器方程,过滤器半径很小(认为这个半径类似于输入数据的空间分辨率)并在非常粗糙的网格上求解它,就在表面。亥姆霍兹滤波器方程本身是线性的,因此可以在任何网格上求解,自适应网格算法将能够识别该网格需要细化的位置。我们只需要对求解器和网格设置进行一些小的调整。
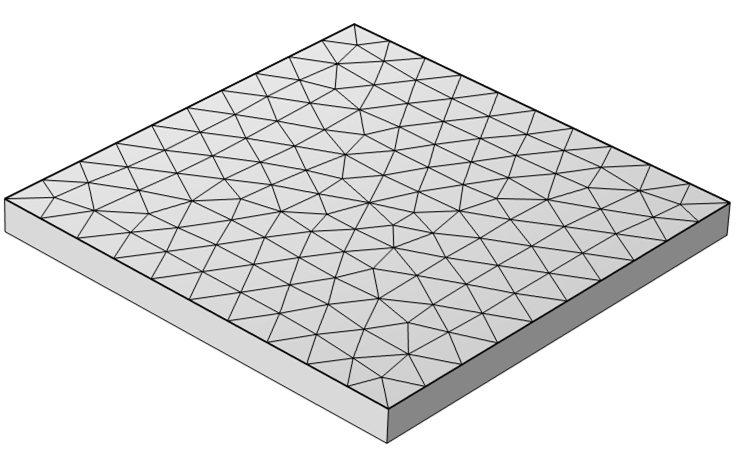
用于启动自适应网格细化的网格仅应用于零件的顶面。
在静止步骤中,我们求解亥姆霍兹滤波器,只需要进行一项更改。必须修改用于自适应的几何实体选择,以便仅在定义过滤器的区域(在这种情况下,只是单个边界)上执行自适应。您还可以选择增加最大适应数并尝试适应方法,尤其是常规修改和重建网格选项。
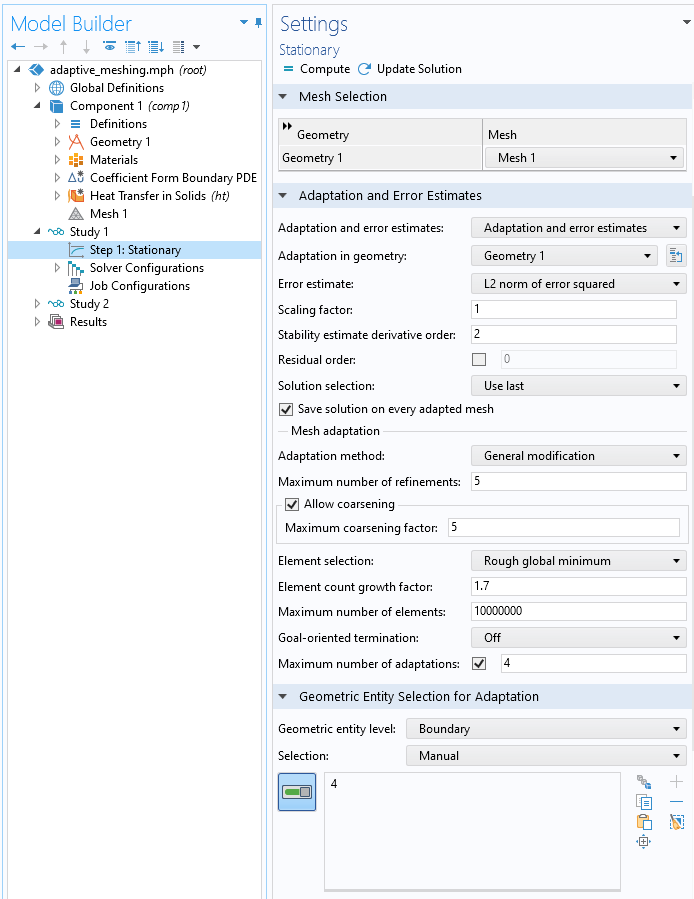
定义边界自适应网格细化的设置。
所有其他设置都可以保留默认值。求解时,我们将获得一系列网格,这些网格仅根据边界上的过滤器解决方案进行调整,如下所示。解算器中可能会出现一些消息,表明体积内没有网格,但这是需要的:我们只想调整表面上的网格,而不是对体积进行任何重新划分网格。

自适应网格细化算法生成的前四个网格的序列。这些仅存在于顶部边界上。
使用自适应网格解决问题
接下来,我们要在用于解决传热问题的体积网格定义中使用一个适配的表面网格。我们需要做的就是添加另一个用户定义类型的网格,并在其中添加一个参考特征,紧跟在网格序列中始终存在的全局尺寸特征之后。之后,我们添加了一个Free Tetrahedral特征,就有了一个完整的网格,它可以被用来解决传热问题。
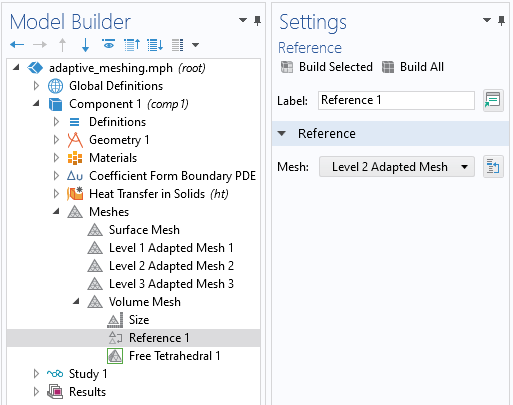
根据先前自适应细化边界网格之一的结果构建新的体积网格。
事实上,从这个网格开始,我们甚至可以执行额外的网格细化。优点是我们已经开始使用非常适合所施加载荷的网格。因此,对于这个问题,我们不需要对热解进行非常多的自适应网格细化。
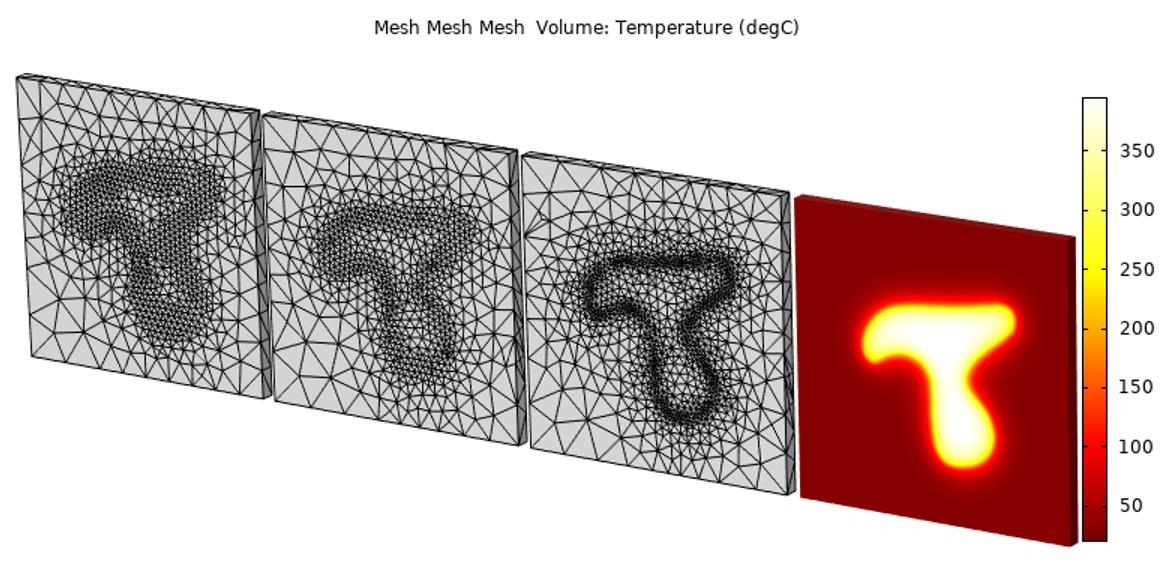
从基于输入数据细化的网格开始,我们不需要多次细化网格来获得对模型解决方案的信心。
我们可以在这里看到,在这种情况下有明显的计算优势。任何时候你正在读入空间变化相当大的实验数据时,研究这种技术都是值得的,因为它可以节省大量的计算工作。另一方面,如果数据相对平滑,没有急剧的过渡,那么就没有必要研究这种技术了。
还值得一提的是,在这种情况下,我们专注于二维平面,因此我们也可以使用将热分布视为图像文件的方法,并将该图像转换为一组曲线,可以在任何二维工作平面。但是,该方法仅适用于二维平面,而此处介绍的方法也适用于曲面甚至体积。
动手尝试
单击下面的按钮,访问与本文中讨论的模型示例相关联的文件:



评论 (0)