
在 COMSOL®软件中,有多种方法可以模拟流体与固体的相互作用。例如,可以使用完整的纳维-斯托克斯方程对压力场和流体速度场进行显式建模。尽管这种方法非常准确,但对于一些流-固耦合问题来说,它的计算成本比实际需要的要高得多。今天这篇文章,我们将介绍一种模拟包含不可压缩流体的封闭腔的方法,假设通过流体的动量和能量传递很小。
编者注: 作者撰写这篇博客的时候,COMSOL 中还没有计算封闭腔中流体载荷的功能。现在,COMSOL Multiphysics®6.2 版本新增了封闭腔功能,可用于计算封闭腔中的流体载荷。
模拟封闭腔中的流体
我们来看一个 COMSOL 案例库中的示例:超弹性密封条的压缩模型。这个示例考虑的是压缩的软橡胶密封件的横截面。腔体中封闭的流体是空气。该示例计算了压缩力,并将密封件中考虑压缩空气影响与不考虑压缩空气影响的结果进行了比较。
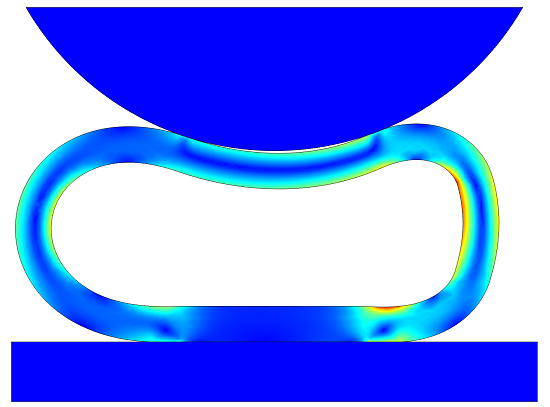
软橡胶密封件的压缩模型。仿真结果显示了应力和应变。使用了不同的方法对密封件内部的空气进行模拟。
示例模型将空气视为可压缩流体,计算了随此二维示例中密封件的横截面积A变化的腔体内部压力p的变化。接下来,让我们来看看它是如何实现的。将腔体内的空气视为绝热压缩下的理想气体,则压力-密度关系为:
\right)^\gamma=\left(\frac{A_0} {A}\right)^\gamma
所以,要计算压力的变化,只需要知道面积的变化就可以了。假设未压缩密封件的面积和压力,以及比热率\gamma均已知,如何计算横截面积呢?该面积由一个我们甚至不想考虑在模型中的区域来描述。使用高斯定理将面积积分转换为边界积分:
其中,x是变形的密封件构型的x坐标,n_x是边界的向外法向量的x分量,也在变形配置中,由此给定密封件的封闭区域。这是通过一个定义在封闭体积的完整内部边界上,名为AreaInt的积分耦合算子完成的。变形区域由在“完整模型”上定义的变量EnclosedArea定义。
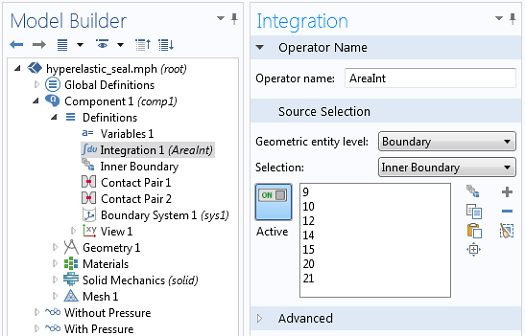
在密封件的内边界上定义面积积分。
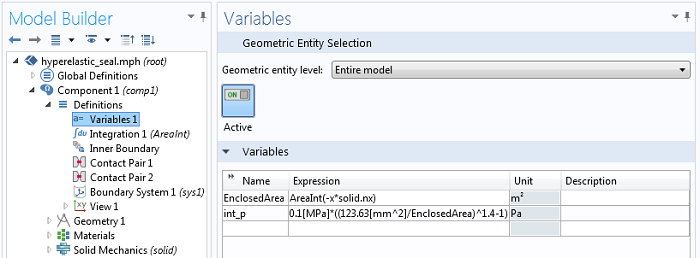
分别定义封闭面积和内部压力的变量的定义。必须使用负号来计算面积,因为固体的法线指向腔体。
计算出的变形面积用于确定密封件变形时内部压力的变化。计算得出的压差作为一个载荷施加到密封件内部。要查看上述方法的完整操作,请查看超弹性密封条模型文档。
考虑不可压缩流体
上述方法假设流体是可压缩的,并且密封件的内部压力与面积变化呈函数关系。但如果流体是不可压缩的呢?假设考虑的不是包含可压缩空气的密封件,而是一个充满水的气囊,其中水几乎是不可压缩的。那么,随着结构的变形,封闭的面积不能改变,上述方法就行不通了。因此,我们需要一个替代方案。
我们将全局方程功能添加到固体力学接口,通过在这个模型中引入一个额外的方程来求解流体内的压力,使体积不会发生变化。我们来看看这个接口:
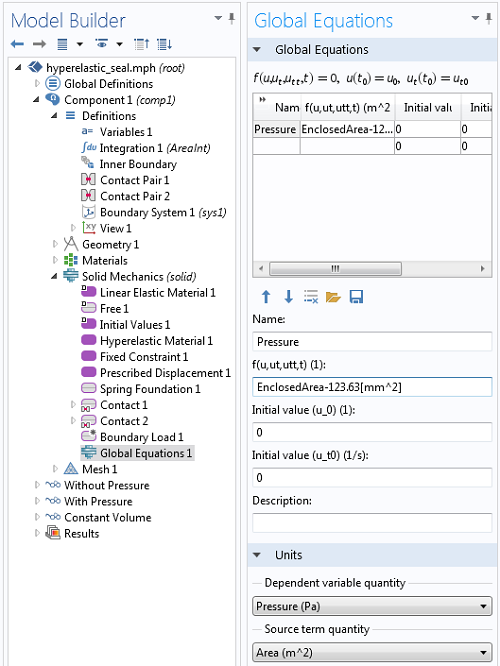
引入的全局方程的设置。需要启用高级物理选项才能查看此功能。
上面的屏幕截图显示了用于额外变量压力的全局方程设置。此方程成立的条件是变量封闭区域等于初始面积 123.63 mm2。也就是说,无论变量压力取何值,都要使变形形状的封闭面积等于初始面积。然后,通过边界载荷功能,将不同压力施加到密封件的内部,并重新求解模型。
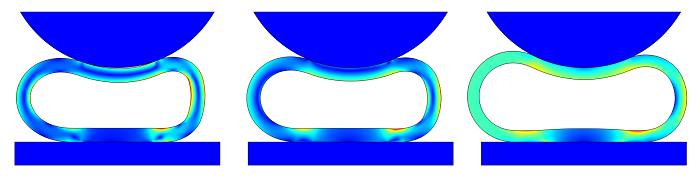
无内部压力(左)、可压缩空气(中)和不可压缩流体(右)时,解的比较。
结束语
文中,我们通过一个示例模型介绍了一种对不可压缩流体和可变形固体的相互作用进行模拟的方法。通过在模型中添加一个全局方程引入了一个额外的变量,来求解维持恒定体积所需的外加压力。这是求解流-固耦合问题的一个最简单的方法。



评论 (4)
广 涂
2023-07-15Hello, I am a graduate student from the School of Energy and Power Engineering of Northeast Electric Power University. Recently, I am studying and reproducing the case in your blog, but when I try to set it as incompressible, the operation encounters Some difficulties, hope to get your help. If possible, I hope you can share the case program after setting it as incompressible. I hope you can reply after seeing it, thank you very much.
My email is:2482592860@qq.com
广 涂
2023-07-15您好,我是东北电力大学能源与动力工程学院的研究生。最近,我正在研究和复现您博客中的案例,但是当我尝试将其设置为不可压缩时,操作遇到一些困难,希望得到您的帮助。如果可以的话,希望您能分享一下设置不可压缩后的案例程序。希望您看到后能够回复,非常感谢。
我的邮箱是:2482592860@qq.com
hao huang
2023-07-17 COMSOL 员工涂 广 , 您好!
感谢您的评论。
关于您问题建议详细描述后联系 COMSOL 的技术支持团队:
在线支持中心:www.denkrieger.com/support
Email:support@comsol.com
谢谢!
兆宇 修
2024-09-03Hello, I am a graduate student at South China University of Technology. Recently, I have been researching and reproducing the case in your blog, but encountered some difficulties when trying to set it to be compressible. I hope to receive your help. If possible, I hope you can share a case program with compressible settings. I hope you can reply after seeing it. Thank you very much.
My email is:2414797194@qq.com