在 COMSOL Multiphysics 中对设计敏感性进行计算

COMSOL Multiphysics 中有一个十分实用却常常被人忽略的功能——计算设计敏感性。假设您用有限元模型计算某个目标函数，那么不论模型输入如何变化，您都能仅仅借助 COMSOL Multiphysics 软件包的核心功能轻松地计算出该目标函数的敏感性。在这篇博客文章中，我们将向您展示这项功能的使用方法。

案例介绍：平行板电容器

我们首先通过一个简单的问题来展开主题：计算两块相互平行的平面正方形金属板的电容，其中金属板的边长 L=1\:m，两块板的相隔距离 D=0.1\:m，夹在二者间的介电材料的相对介电常数 \epsilon_r= 2。假设边缘场可忽略不计（一个相当严苛的假设，不过在这里我们以该假设为出发前提），电容的解析表达式可以写成：

其中 \epsilon_0 表示自由空间的介电常数。

接着我们可以方便地对由上述三个输入得到的表达式进行微分，并以此找到设计敏感性：

接下来我们将讨论如何使用 COMSOL Multiphysics 的相关功能对类似的敏感性进行计算。

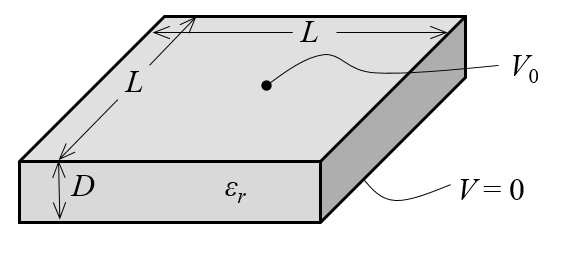
忽略边缘场时的平行板电容器模型示意图。

首先，通过 静电 物理场接口创建一个模型。我们创建了一个长度与深度均为 L ，高度为 D，且相对介电常数为 \epsilon_r 的长方体域，同时将长方体底部的边界条件设为 接地 条件，并在其顶部施加 电势 条件并将电压设为 V_0=1\:V。对长方体的侧面默认执行 零电荷 边界条件，这一设定相当于忽略了边缘场。这样我们便能对模型进行求解并获取两块板之间的电压场。根据求解结果，我们便能基于整个模型的电能密度积分 W_e，最终计算出系统的电容值：

上述方程基于如下假设：一块金属板（或终端）始终被施加了电压 V_0，而模型的其他终端皆处于接地状态。我们已经通过内置变量 comp1.es.intWe 计算出了全部域的电能密度积分，接着便可基于积分结果来定义所计算电容的表达式。当然，我们之后会将电容值及其敏感性同上文的解析值进行对比，以便给这些物理量定义相关变量。在进行对比之前，我们可以使用内置的微分算子 d(f(x),x) 计算精确的敏感性，如下图所示。

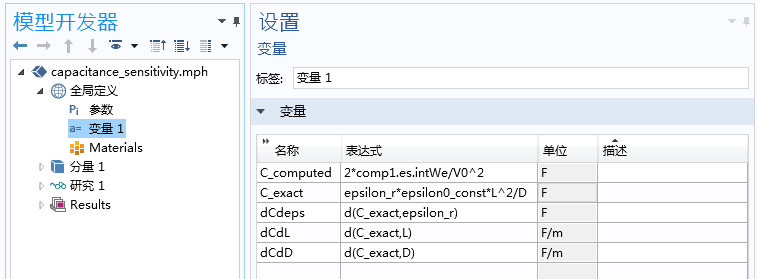
这些变量被用于计算模型的电容、精确电容及其敏感性，例如 d(C_exact,L), 等内置的微分算子可用于计算精确的敏感性。

在完成模型求解后，我们可以计算所求解系统的电容，将其与解析值进行比较，从而分析计算出设计敏感性。现在让我们看看如何利用 COMSOL Multiphysics 来计算这些敏感性。

就参数而言，它们不仅影响模型的材料属性，还影响几何尺寸。如果设计参数影响到了几何结构，则需要用到变形几何 接口，它能让我们计算对于几何变形的敏感性。

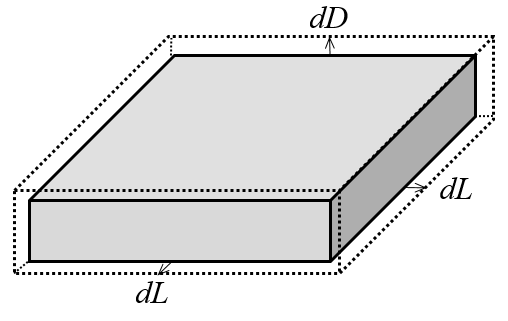
如图所示，设计参数会对几何结构的变化产生影响。隐藏的几何面没有沿边界法向发生位移。

接下来，我们将引入两个新的全局参数：dL 和 dD，它们分别表示 L 与 D 的变化量。这些参数将用于包含四个相关特征的变形几何 接口中。首先，域中应用了自由变形 特征，这意味着计算区域将基于应用的边界条件而产生变形。其次，域的六个面应用了指定网格位移 特征。在下方截图中，沿面法向的变形（dL）按上图所示来指定。

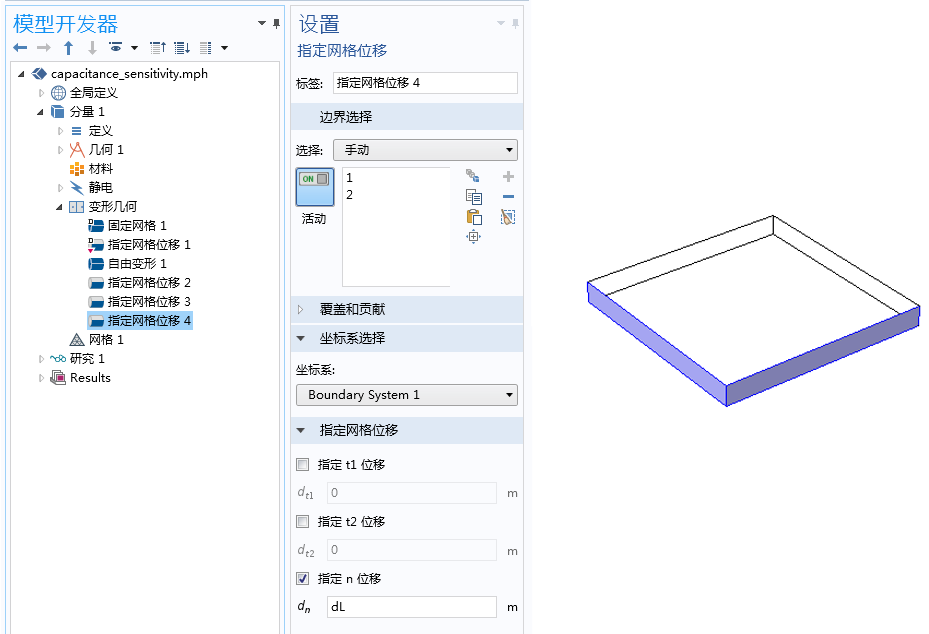
指定网格位移 特征用于控制各域边界法向位移。

最后，为了实际计算敏感性，我们必须将敏感性 节点添加到“研究序列”中，如下方截图所示。您可以输入如该例中 C_computed 的目标函数表达式，也可以输入您在研究中感兴趣的所有设计参数。另外，请围绕所要计算的敏感性来输入设计参数值。因为 dL 和 dD 表示尺寸增量，所以我们可将二者均置为零来计算 L=1\:m 且 D=0.1\:m 时的敏感性。最后，除了要将其选为“敏感性”研究中的参数之一，用于控制材料介电常数的参数无需其他特别的设置。

下方表单中列出了梯度方法的两种选择：

• 伴随 法更加高效，并且其求解时间不受研究中的参数数量的影响。事实表明，伴随法仅仅增加了相当于总计算成本中的一次牛顿迭代。
• 向前 法的求解时间会随着参数的增多而增加，不过该方法确实能够额外返回整个解物理场的敏感性，因此更适用于一些特定情况。

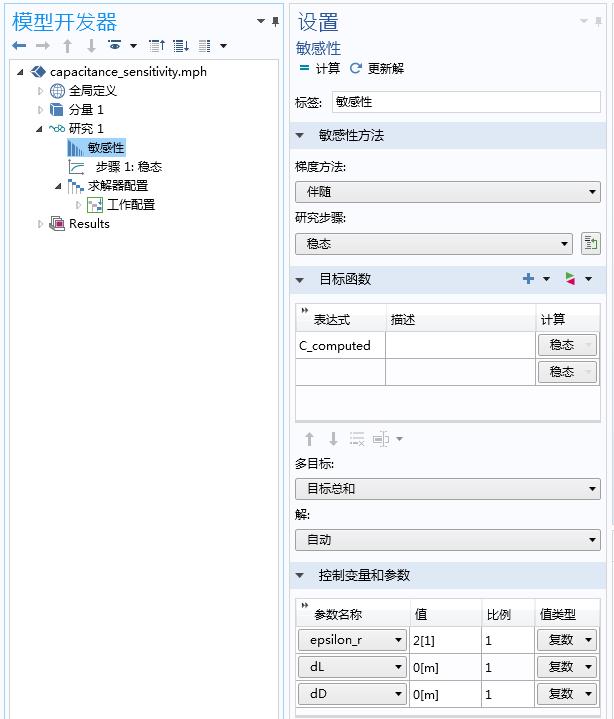
将采用了伴随法的“敏感性”特征添加至“研究”序列，图中的设置显示了目标函数和需考虑的参数。

在求解完毕后，您就能前往结果 > 派生值 > 全局计算，并输入表达式 fsens(dL)、fsens(dD) 以及 fsens(epsilon_r)，从而计算出当前设计参数下电容的敏感性。当然，您还可以将结果与之前计算的敏感性解析值作对比，并查看二者一致性。

到这里，我们已经基本了解如何计算系统电容的敏感性。我们还能实现其他操作吗？回答当然是肯定的，我们可以继续利用本节介绍的知识去处理一些更为复杂的几何结构。但是在案例结束之前，我们还要牢记几个需要注意的点。

计算设计敏感性的局限和应用范围

顺利执行敏感性分析必须满足两个前提条件：第一，目标函数必须是关于解物理场可微分的，这意味着表示场最大值与最小值等类型的目标函数不适用；第二，参数在实数空间内必须是连续的，因此整数参数（例如车轮中辐条的数量）不适用。

特征值问题、射线追踪和粒子追踪目前不能使用敏感性计算。

设计参数本身是典型的“全局参数”，但是您也可以根据需要，使用敏感性 接口添加定义在域中及边界、边和点上的控制变量场。

目标函数通常以解的积分的形式定义在域内或边界上。我们也能够在模型空间的某一特定位置上建立作为探针 的目标函数，而任何基于解物理场的派生值（例如解在空间上的梯度）都可用作目标函数的一部分。

结束语

借助计算设计敏感性这一功能，我们可以有效地确定对目标函数的影响最大的参数，进而让我们在开始修改设计就能找到那些应重点关注的参数。其他使用了这项功能的案例还包括轴向磁轴承教学模型和通讯天线塔细节的敏感性分析教学模型。当然，该方法的使用情况远比本文介绍的更为丰富。

在后续的案例中，我们会进一步通过使用这些敏感性来改进目标函数，从而实现设计优化，这一操作可通过优化模块实现。我们将在即将发布的博客文章对此进行详述。