
当你在观看怪兽题材电影时,有没有想过:如果地球上真的存在巨型怪兽会怎样?为了找到保护人类的有效方法,来自卡迪夫大学(Cardiff University)和牛津大学(University of Oxford)的两个数学生物学家使用数学建模对电影中常见的消灭这些巨型怪兽的方法进行了测试。通过对仿真结果的分析,他们还进一步确定了适用于不同地区的最佳策略。
基于种群生态学理论研究如何消灭巨型怪兽
一个科学考察队在探索马里亚纳海沟(Mariana Trench)深处时,意外地从温跃层的裂缝中释放了一只史前巨鲨——巨齿鲨。随后,他们耗费了大量武器、技术和船员来追捕这头巨鲨。在另一个类似的虚构故事中,一头体型庞大的大白鲨用它锋利的牙齿威胁度假岛上的人类……直到主角将它击败送回海底深处。
《大白鲨》(Jaws)的拍摄地点位于美国马萨诸塞州的马撒葡萄园岛(Martha’s Vineyard, Massachusetts),科德角海岸附近。在真实世界中,近年来鲨鱼的数量一直在迅速增长。虽然鲨鱼袭击人类的事件远比电影中展现的要少得多,但当人们看到海滩上出现大量背鳍时,仍然会感到担忧。那么,究竟是什么原因导致这么多的大白鲨靠近海岸呢?

大白鲨。图片由 Olga Ernst 提供自己的作品。通过Wikimedia Commons在CC BY-SA 4.0下获得许可。
简单来说,海豹数量的减少是导致这个问题的主要原因。在1880 年代到 1960 年代,由于海豹会捕食鳕鱼,新英格兰渔民便将其视为渔业的威胁,因此大量捕杀海豹,直到该地区的海豹数量有明显减少。之后, 1970 年代颁布的《海洋哺乳动物保护法》(Marine Mammal Protection Act)中将杀死海洋哺乳动物定为非法行为,这才使得海豹的数量有所回升…… 以海豹为食的鲨鱼数量也随之增多。
一些人提议捕杀海豹,另一些人提议捕杀鲨鱼,但通过捕杀这种方法可能会使问题变得更加严重。如何预测哪些选择会产生预期结果,哪些选择会带来意想不到的后果呢?其中一种方法就是运用数学方法研究生物学。
种群生态学理论
为了激发人们对真实生活中的生态问题(如大白鲨重返海角)的兴趣,数学生物学家 Thomas Woolley 博士和 Philip Maini 教授将目光转向了惊险刺激的怪兽电影。他们基于《环太平洋》(Pacific Rim)、《侏罗纪世界》(Jurassic World)、《哥斯拉》(Godzilla)和《金刚》(King Kong) 等各种类型的电影所发现的“证据”,将理论种群生态学数学应用于一个研究名为Kaijus的巨型怪兽和 Jaegers巨型机器人的虚构场景中。在下文中,您将看到这些典型的证据可以指导他们确定仿真参数。
尽管这一研究所需要考虑的问题有很多,但其基本原理仍围绕着自然界已经发现的理论:种群动态。对于 Woolley 而言,使用电影类比来吸引人们对种群生态学产生关注是一个很好的切入点,他说:“我们如何才能以最好的方式将研究的东西展示出来呢?”人们可以很容易地以僵尸灾难与疟疾或流感的传播进行比较,因为它们的数学模型是一样的。而对于怪兽题材来说,生物学家们关注于物种间的竞争,捕食者与猎物之间的相互作用,以及人类尝试灭绝物种等。
使用 COMSOL Multiphysics®软件内置的捕食者-猎物方程等常用工具,可以对生态害虫问题进行研究。该方程的官方名称为 Lotka–Volterra,它从数学上描述了两个物种相互作用的方式,其中一个是捕食者,另一个是猎物,以及它们的种群随时间的变化情况。研究人员以捕食者-猎物的相互作用问题为基础,对上文提到的 Kaijus 巨型怪兽进行了仿真计算。
kaiju 巨型怪兽种群的数学建模
在制定消灭策略之前,生物学家根据以下主要标准为 Kaijus 定义了预测种群规模的参数:
- 相互作用
- 行动路径
- 环境边界
- 初始分布
怪兽 Kaiju 的设定表明,这些生物不仅具备繁殖能力,当种群数量过多,必须为资源竞争时,它们还会自相残杀。因此,科学家们在模型的交互部分使用了逻辑斯蒂增长微分方程。在现实生活中,这类方程可用于描述从酵母到狼等各种生物种群。
在移动方面,科学家们基于流行电影中这些怪兽的能力,确定它们能在不到一天的时间内从海洋移动到陆地,并根据从环太平洋沿岸到日本(约 1000 英里)所需的 24 小时时间周期来计算它们的移动速度。他们发现,Kaijus 能以大约每小时 40 英里的速度游泳。作为自然力量,Kaijus 倾向于从起点随机移动到最近的陆地。这有助于科学家们根据怪兽密度的扩散和时空演变推导出偏微分方程。此外,他们还考虑了怪兽可以改变方向的情况,尤其是在遇到边界时。
虽然 Kaijus 可以通过陆地和海洋移动,但一旦上岸,它们很少会返回海洋。在最坏的情况下(例如,假设外星人持续不断地派遣这些怪兽来摧毁我们),将选择具有反射性(Neumann)作为环境边界条件。边界条件将被归类为源项,科学家们也在他们的方程中考虑了这一点。
至于初始分布,由于怪兽的来源未知,科学家们假设最坏的情况:怪兽会在陆地上肆意活动至承载极限,即一个地区所能支持的最大生命密度。

一部怪兽题材电影的剧场海报。该作品属于公有领域,于 1924~1963 年在美国出版,尽管可能有也可能没有版权声明,但版权并未续签。除非其作者在规定时间内已去世,否则它就不适用于美国作品短期期限规则的国家或地区拥有版权,如加拿大(50 pma),中国大陆(50 pma,而非香港)或澳门),德国(70 pma),墨西哥(100 pma),瑞士(70 pma)和其他有个别条约的国家/地区。有关更多说明,请参见Commons:Hirtle chart。图片来自Wikimedia Commons。
既然我们已经知道了它们的种群参数,那么在电影中最常用的消灭它们的方法是什么呢?是部署 Jaegers,还是创造我们自己的 Kaiju?无论哪种方式,Woolley 和 Maini 都知道他们需要在不同的区域研究不同的方法。
因为这是一个虚拟的系统,所以数学家使用了一种相对落后的方法来展示如何运用数学处理同时存在不同假设情况的问题。Woolley 问:“您是想要毁灭它们,还是要让它们存活下来?”答案取决于怪兽所占据的面积,以及怪兽所处的位置:怪兽是占领了一个岛屿,还是遍布整个大陆?研究人员分别对三种不同大小的陆地进行了仿真测试:英国是代表小型陆地,日本代表中型陆地,美洲(南部和北部)代表最大的陆地,并为这三种不同大小的陆地探寻不同的解决方法。
Woolley 还说:“对于像日本这样的中型国家,很有趣的是,它接近一个“分叉点”。在这个分叉点上,Jaegers 很容易成功,但也很容易失败。”数学生物学家认为,也许这就是为什么有那么多关于巨型怪兽的电影都来自日本的原因。根据对每个地区的研究结果,我们将看到,数学家们为日本提供了一个首选策略。
使用 COMSOL Multiphysics®消灭巨型怪兽的 2 种策略
为了解 Jaeger 的部署或 Kaiju 的创建对这三个区域的影响,该团队建立了所需的模型和方程,如无量纲化以预测域大小,稳定性分析和扩散引起的不稳定性等。Woolley 解释说:“我们在 MATLAB®软件中运行了小型的概念证明模型。由于 COMSOL®具有所需的编码,我们通过LiveLink™ for MATLAB接口直接运行整个模型即可。
Woolley 表示,COMSOL Multiphysics®具有他们所需的所有方程,并且能够一致、快速且反复地计算扩散方程,同时保证计算结果的质量。另外,他们还能够将三个地区的地图导入MATLAB®软件中,然后将生成的数据用于COMSOL®软件中并创建几何图形。


怪兽 Kaiju(左)和机器人 Jaeger(右)。插图由 Thomas Woolley 提供。
1.派出 Jaegers 巨型机器人
数学家提出的第一个策略是部署巨型机器人,无论它们在哪里出现,都会与怪兽作战。经典类怪兽电影已经证明了 Jaegers 的强大足以在他们倒下之前终结许多怪兽,而且通常一次部署一个 Jaeger 就可以抵御数只怪兽。尽管 Jaeger 造价昂贵,难以建造并且具有危险性,但它们可以被完全控制。这使得这种选择比在某些情况下制造另一种怪物更可行。
这些机器人被模拟为点源,并将它们固定在空间边界的地方,以尽量减少人类伤亡,并观察等待怪兽出现需要多长时间,以及确定机器人的位置。
在运行了部署 Jaeger 的仿真后,结果表明,由于 Jaegers 的局限性(作为单个战士被派遣去抵御许多怪物),它们仅能够保护诸如英国这样的小型国家。如下所示,一旦 Jaegers 被部署,他们可以在大约 24 小时内大幅减少 Kaiju 的数量。
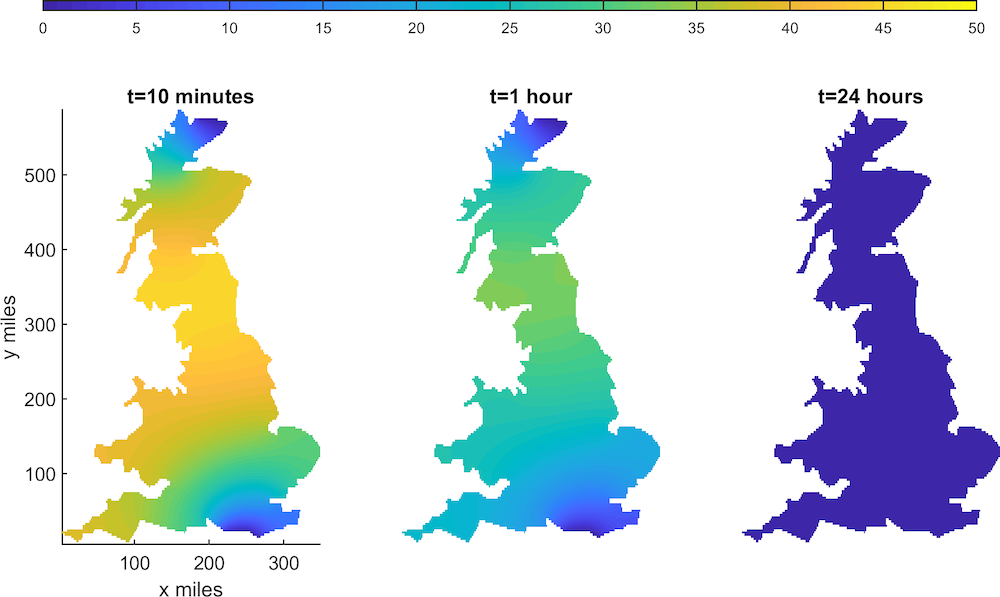
Kaijus 在英国境内的密度分布随时间的变化,其中 Jaegers 被置于苏格兰北部和英格兰南部。浅色阴影区表示 Kaijus 密度较高,而深色区域表示密度较低。顶部颜色图例的单位为数千吨。图片由 Thomas Woolley 提供。
如果是像日本这样的中型国家,Jaegers 的部署范围变得更狭长了。如果只给它们 24 小时,它们仍然可以消灭很多 Kaijus,但不能完全清除。然而,如果给定它们 70 个小时,他们可以将 Kaiju 的数量减少到零。
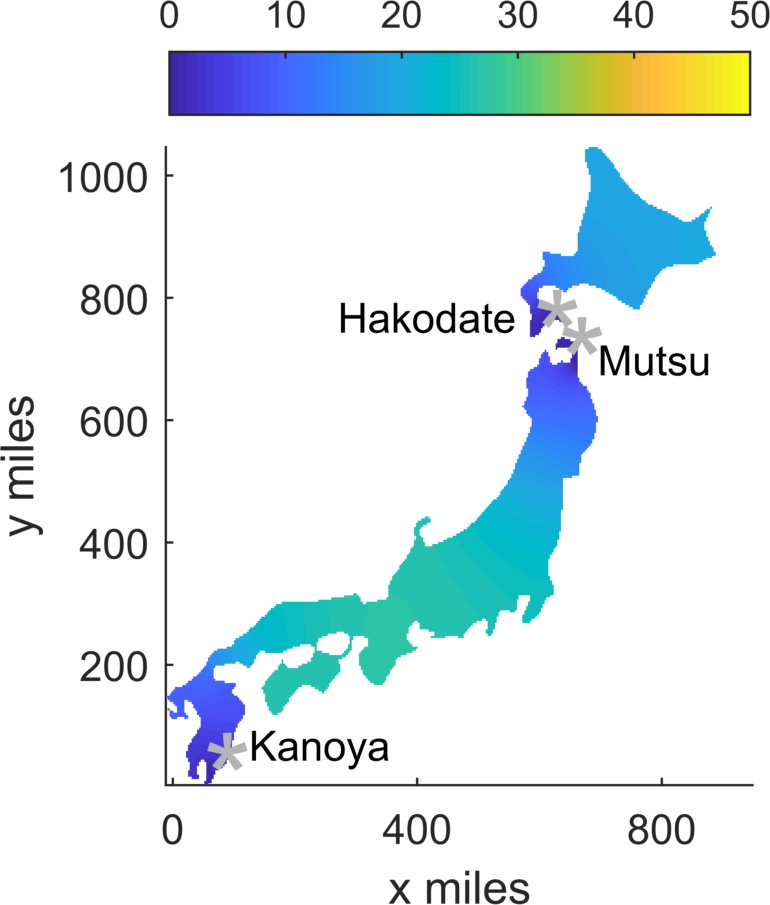
Kaijus 在日本的密度分布数量随时间变化的情况。其中 Kaijus 置于标注位置。在 24 小时模拟中,怪兽的数量趋于稳定,但并没有消失。
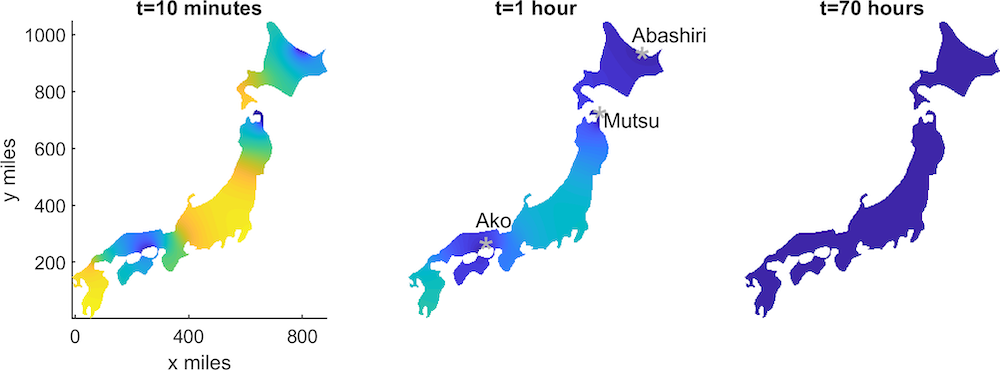
但在 70 个小时后,Kaiju 被消除了。颜色图例的单位为数千吨。图片由 Thomas Woolley 提供。
对英国和日本的研究结果表明,Jaegers 适合于较小的区域,即使只在这些区域的边界处派出大型机器人作战,也可在合理的时间内击退所有怪兽。然而,由于能够生产的机器人数量有限,如果 Kaijus 入侵的面积超过这些岛屿,可能就需要采用另一种策略了……
2.创造一个比 Kaiju 更强大的捕食者
另一种选择是通过辐射(如电影经常描绘的那样)对生物进行基因改造,然后将其释放到现有的 Kaijus 中,这种突变体必须比其他怪兽更强大。但是,数学家说用这种方法需要小心处理。首先,即使是训练有素的怪物仍然比巨型机器人更难控制。其次,作为新生物界的顶级捕食者可能使问题变得更糟。我们在现实生活中也碰到过类似的问题,如人类为了根除一个物种,而向此生态系统中投放该物种的捕食者,这种方法有些获得了成功,有些则失败了。
考虑到这些注意事项,科学家们认为,突变的 Kaiju 需要比其他种类的怪兽更强壮,速度更快,寿命更短,且它不能对人类具有攻击性。这些参数使我们能够更安全、更有效地将突变体 Kaiju 部署到更广阔的土地上。在不依赖我们控制的情况下,它们可以进行繁殖,可以捕杀现有的 Kaijus。此外,数学生物学家利用动力学知识和其他参数,为我们的新生物提供了空间非均匀峰值解决方案,这意味着掠食者与猎物之间的相互作用将产生一个局部稳定的生态系统,这样我们的怪兽可以茁壮成长,但仅在它们的局部巢穴范围内。如果这些巢穴远离人类种群,我们可以与它们共存,直到自然消亡,那这会是一个更加人道的选择。
在运行模拟后发现,即使我们的突变体有足够的速度和捕猎本能,能在大范围内追捕猎物,但捕食者-猎物方程告诉我们,这样两种种群的数量最终将会达到平衡。提高突变体的速度有助于减少现有的怪兽的数量,但并不能完全消灭它们。结果表明,当我们提高突变体的速度时,它们会采取猎杀和围困策略,将 Kaiju 驱赶至更小的区域。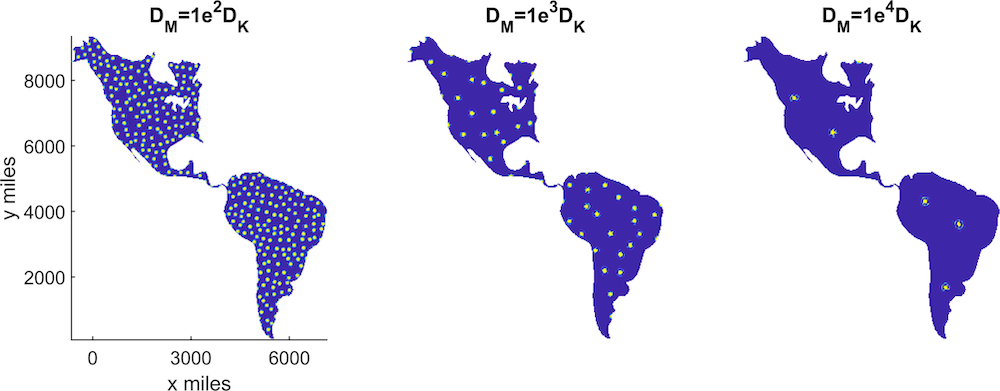
Kaiju 在北美和南美的密度分布,深色阴影表示低密度,浅色阴影表示高密度。从左到右的图分别表示我们的怪物的速度逐渐增加。图片由 Thomas Woolley 提供。
一旦科学家们认为在更大的陆地上,突变体怪兽比 Jaegers 更有效时,他们转而就会考虑:哪种类型的生物最适合进行基因突变呢?为了探究这个问题,科学家们根据一部怪兽电影,寻找到了一种名为Mothra的飞蛾。事实证明,Mothra 有击败哥斯拉的记录。她比 Kaijus 更有才智,更有侵略性,且对人类更加和平。此外,飞蛾的飞行速度极快,但寿命很短。因此,Mothra符合优质捕食者的标准。

Mothra。插图由Thomas Woolley提供。
尽管研究人员提出的不同的策略可应用于不同的区域,但是他们得出了一个结论:一旦 Kaiju 的数量处于一种更易于管理的情况,则可以采用多种策略解决问题。首先我们的突变体将 Kaijus 赶到很小的一片区域,随后即可在这些区域部署 Jaegers 并将 Kaijus 彻底消灭。不过,这会导致突变体失去食物来源,迅速灭绝。科学家们也承认,这意味着这些被创造出来的怪物在绝望时可能会捕食人类。因此,为了安全起见,我们最好植入一个自爆装置作为备用方案。
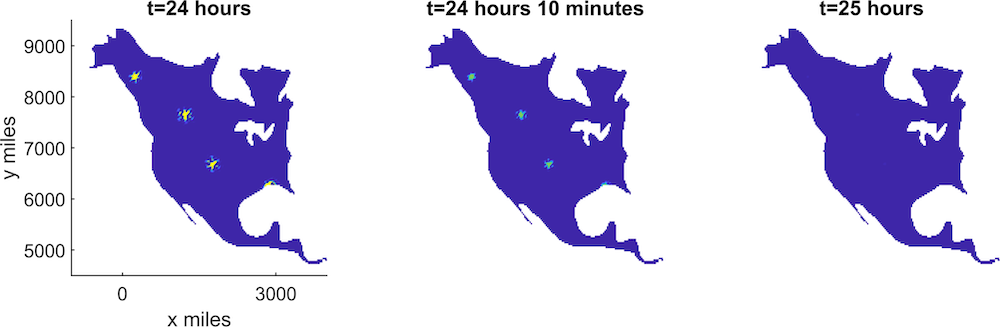
一旦突变体将 Kaiju 聚集在北美,就派 Jaegers 去消灭它们。从左到右表明,随着时间的推移,Kaiju 逐渐被消灭。图片由 Thomas Woolley 提供。
回到现实
通过使用 COMSOL Multiphysics,Woolley 找到了使数学更易于理解,并对他的同事有意义的方法。虽然这一虚构的例子很有趣,但 Woolley 也将他的研究应用到了现实世界。他将该方法应用到了模式形成和细胞理论研究。现在,他正在研究其中一个项目,钙信号传递及其如何扫描鸡蛋,并使用3D全波方程研究鸡蛋的完整形成过程。
此外,他还为脊柱肿瘤、大脑成像和肿瘤运动创建了图形用户界面(GUI)。就像虚拟场景中的地图一样,研究人员可以将大脑的形状直接导入 COMSOL®软件中进行脑肿瘤研究,导入方法简单、快速且高效。
“ COMSOL 使我可以朝着自己的方向前进,而不必每次都构造自己的专用代码,” Woolley 说。无论是将数学模型用于现实生活研究还是虚构情景中,都可以节省时间使我们专注于真正重要的事情。
根据模拟结果来看,如果有怪兽入侵,我们遵循科学家的策略应该是安全的。不过,为了应对未来的威胁,还是有一些需要改进的地方。毕竟,正如《侏罗纪公园》(Jurassic Park)中虚构的数学家 Ian Malcolm 博士所说的,“生命自有出路(Life, uh, finds a way)”。
MATLAB 是 The MathWorks,Inc. 的注册商标。



评论 (0)