
在之前的博客文章中,我们研究了一种计算声辐射力的扰动方法。这种方法的优点是既稳定又快速,但是它在很大程度上依赖对正确扰动项的理论计算。本文将介绍另一种求解方法,即从与固体弹性微粒相互作用的纳维-斯托克斯方程组的完整非线性解中推导出辐射力。
流固耦合(FSI)公式
我们要解决的问题包含由声波引起的流体运动,以及流体流动对固体粒子施加的力。粒子受力会产生变形和运动,并对流体产生反作用力。这意味着,除了求解描述流体动力学的方程外,还需要考虑粒子的变形以及由此产生的流体所占空间的变形。在COMSOL Multiphysics®中,我们可以通过软件预置的流-固耦合物理场接口将流体流动、结构应力分析和网格变形进行耦合来解决这个问题。
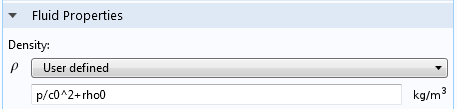
声辐射力是一种非线性效应,其中的非线性是流动固有的,来自纳维-斯托克斯方程中的对流项(\mathbf u \cdot \nabla )\mathbf u,而不是来自材料非线性。为了与声波假设相容,流体必须是可压缩的。流体可压缩性可以通过修正流体的本构关系来引入。假设有一个线弹性流体p = c_0^2(\rho-\rho_0),对于水,设置c_0= 1500 m/s 和\rho_0= 1000 kg/m3。因为我们起初是想将这个方法与忽略黏度影响的经典分析模型进行比较,所以假设一个任意的、小的黏度值。
驻波场中的声辐射力要高得多,利用这种效应的大多数应用都涉及驻波。我们来看看这个案例。
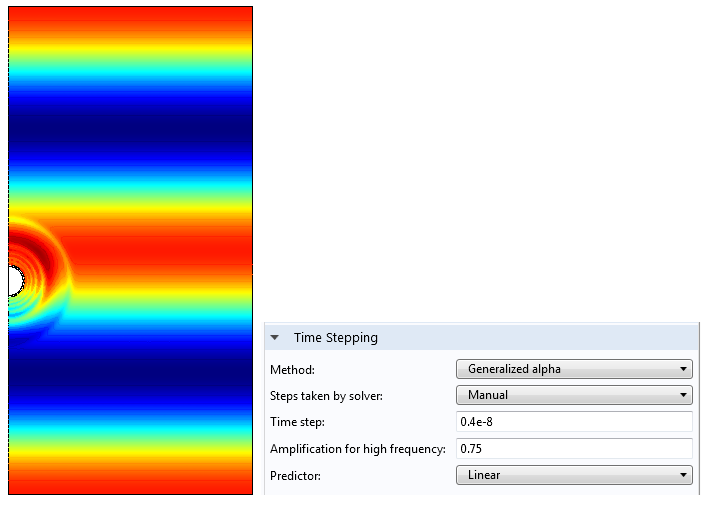
因为这个问题是非线性的,所以必须在时域中求解。求解过程可能非常耗时,因此我们将求解一个二维轴对称几何模型。为了在瞬态解中创建驻波,考虑一个高度是两个波长的谐振箱,并通过设置相应的初始条件来启动驻波。例如,在一个高度为两个波长的谐振箱里,驻波解将为p(r,z,t) = p_0 cos(k_0 z) cos(\omega t),并且当t= 0时,初始条件应该是p(r,z,t=0) = p_0 cos(k_0 z)和\mathbf u(r,z,t=0) = 0。下图为一个高 3mm,波长\lambda= 1.5mm(相应频率为 1MHz)的模拟箱。

就像上一篇博客中所说的,我们期望非线性力项比线性力小几个数量级,这样粒子就会在声场中上下弹跳。然而,每次粒子移动时,它都会在一个方向上比另一个方向走得更远。这是非线性力分量的结果,当场改变符号时,非线性力分量的方向不会改变。由于非线性力非常小,因此很难从时域解中提取非线性力的值,除非使用一个非常简单的技巧。
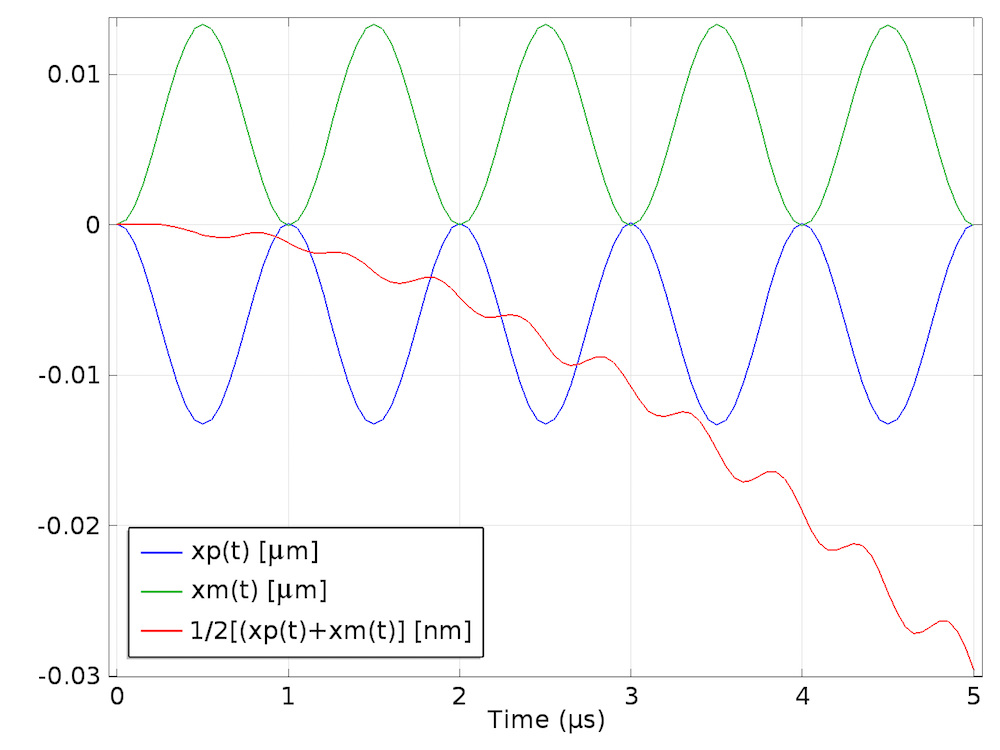
这个技巧的本质是基于这样一个事实,即当激励符号改变时,非线性力方向不会改变。当p_0为正时,将x_\textrm p (t)表示为粒子获得的平均位移,当p_0为负时,将x_\textrm m (t)表示为粒子获得的平均位移。用两者的组合x_\textrm{nl}(t) = 1/2 \left [ x_\textrm p (t) +x_\textrm m (t) \right]表示非线性位移分量。这种方法是在这篇文章中被首次提出的。下图显示了压力幅值为 0.1MPa,半径为 100μm 的尼龙粒子的解。可以看到,x\textrm p (t)和x_\textrm m (t)的符号相反,否则看起来应该相同;但是,它们的总和不为零,尽管很接近。
动画显示了粒子的运动。
关于在 COMSOL Multiphysics®软件中实现的说明
上面概述的方法考虑了非线性声学现象。因此,以下列出的声学仿真的通用规则都适用:
- 网格必须足够精细,用于分辨最短的波长。这里,基本波长是外部施加的驻波波长。然而,较短的波长是由粒子以其共振频率振动产生的。这些波长将被模型捕获,因为它是在时域中求解的。
- 在 COMSOL Multiphysics 中求解波现象时,一种合适的时间步进方法是广义α法。为了确保解稳定,必须通过设置手动施加 Courant–Friedrichs–Lewy(CFL)准则,方法是手动设置步长为\delta t < 0.5\ h_\textrm{min} / c_0。
后处理
分析的最后一步是根据有限元模型给出的平均非线性位移计算力。我们可以观察到声辐射力的影响,即从粒子的其他完美振荡运动中产生的位移的微小偏移。从计算出的位移线性分量和非线性分量的差异来看,力分量的差异大约为三个数量级。因此,在一个声学周期内,声辐射力的影响可以忽略不计,为了正确计算它,必须计算大约五到十个声周期。
有了这些数据,我们就可以将结果导出到 Excel®电子表格软件中,并通过对位移曲线进行二阶多项式拟合将力计算为F = m \ddot x_\textrm{nl}。下图是分析的结果。
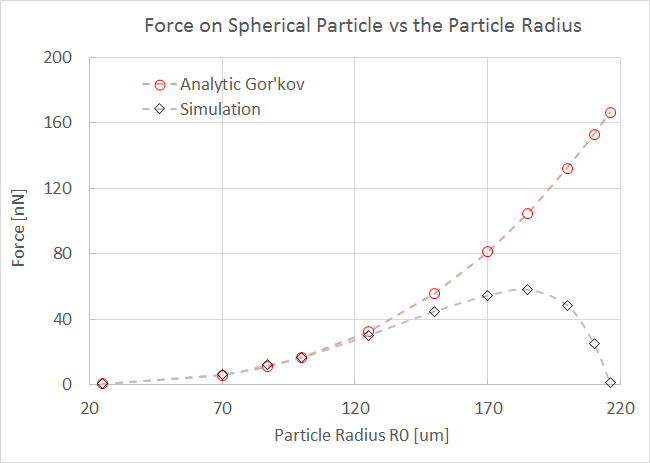
这里,距驻波节点 λ/8 处的最大压力被评估为粒子半径的函数。在微粒很小时k_0R_0 \ll 1,解析解是有效的,并与仿真结果获得了很好的一致性,当不满足这个限制时,偏差似乎会增加。
结论
本文概述了一种计算非线性声辐射力的直接方法。同样的方法可以应用在其他非线性声学效应中,例如声流。这种方法的优点是它不依赖于任何理论模型(例如,扰动方法)来表达非线性项。请注意,由于流-固耦合方法要求在时域中求解模型,因此它比扰动方法要慢得多。
声辐射力系列的其他博客
Excel 是微软公司在美国和/或其他国家/地区的注册商标。



评论 (0)