
你有没有遇到过这样的情况:无论将几何拐角处的网格细化到什么程度,所计算的电磁场似乎都不会收敛。如果有,你将如何处理?在今天的博客文章里,你可以找到解决方案。
尖锐棱角的奇异电磁场
以一个弯曲铜导线模型为例来说明。如下图所示,我们对该铜线模型两端施加了 5mV 的电压,模型计算了流经铜线的总电流。使用默认的常规网格,我们将获得 490A 的电流。为了确定该电流的精度,我们尝试了其他一些网格设置,所得计算结果仅相差几毫安,并且在较细的网格之间差异明显较小。因此,我们判断结果是收敛的,并且网格足够满足我们的需求。
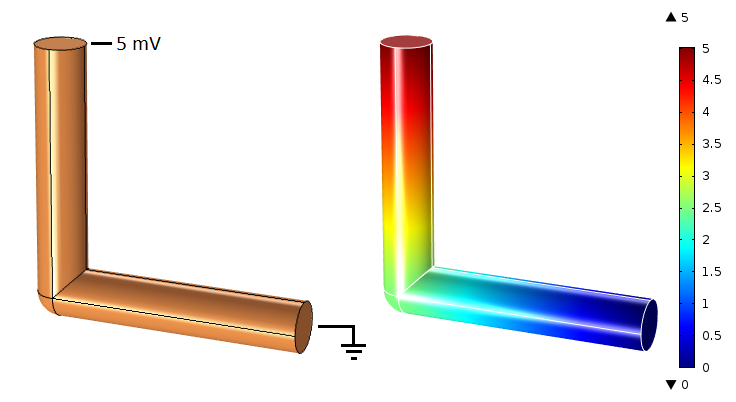
铜导线模型设置(左)和以毫伏(mV)为单位计算的电势分布(右)。
接下来,我们来评估导线中的最大电流密度。这个值不能太高,如果太高,产生的热量有使保护套磨损的危险,甚至有潜在的火灾隐患。
使用普通网格可以得到的最大电流密度为 6.2A/mm2。很明显可以看出,这个值出现在内弯角处,因此我们在该区域使用了细化网格。下图显示了细化网格后的计算结果(非常令人吃惊):即使将网格细化 100 倍,最大电流密度仍在增长,并且没有迹象表明它将停止。
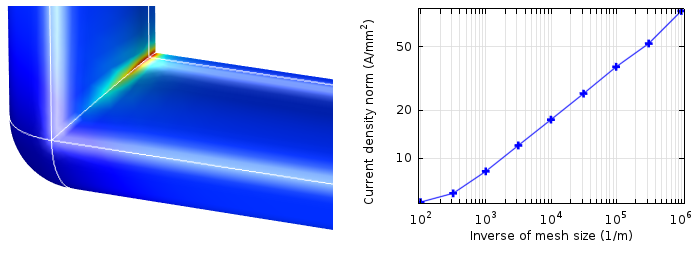
内弯角的奇异电流密度(左)和计算出的最大电流密度与局部网格密度(右)的关系。
这是一个几何奇异结果。电流密度与电场成正比,电场又是电势梯度的负值。尽管电势在棱角处保持平滑且定义明确,但理论上棱角处的电势梯度是无穷的。在数值上,当我们细化网格时,它将趋于无穷大。实际上,当然没有完美的棱角。但是,棱角处越锋利,局部电流密度就越大。
在 COMSOL Multiphysics®中创建圆角
如果将棱角创建为圆角,就可以限制模型中的电流密度,更好地模拟现实情况。
我们可以这样操作:
- 创建在边缘处相交对象的并集,确保清除保留内部边界复选框。这样可以使倒圆角的方向明确。
- 添加圆角节点。选择要包括的边并提供合适的半径。
- 单击构建所有对象查看结果。
将棱角设置为圆角后,模拟结果回到了平滑的电流分布,收敛的最大电流密度值为 5.1A/mm2。
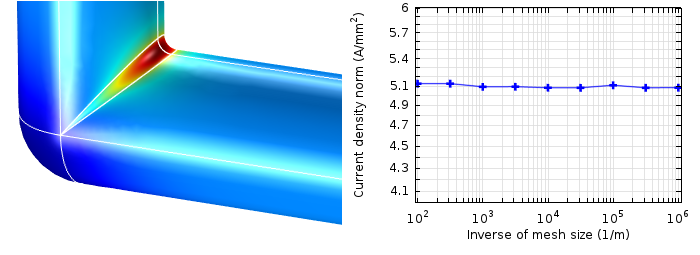
平滑电流密度分布(左)和计算所得圆角的最大电流密度与网格大小(右)。
是否要设置为圆角?
如果你只对总电流、电压分布或离奇异点较远的电流密度感兴趣,那么即使没有圆角,也可以获得良好的结果。重要的是,这也适用于集总参数,例如电阻和阻抗。在电磁加热模型中,尽管只有局部具有奇异的电流密度,即使给定很小的热导率也能够得到平滑的温度分布和最高收敛温度。
不过,如果你想正确处理局部电场和电流,那么保持平滑是一个好方法。通常,3D 模型中的边缘和角以及 2D 模型中的角可能会产生奇异的电场或磁场。如果它们都标记了模型的外部界限,或者它们分开了具有不同属性的材料,这种奇异是成立的。如果场是奇异的,则大多数显式且局部依赖于它们的变量也是如此。
下图像显示了马蹄形磁铁旁边的铁条表面的麦克斯韦应力张量。由于应力张量与磁场的平方成正比,因此如果铁条的棱角和边缘尖锐,则应力张量将变得奇异。
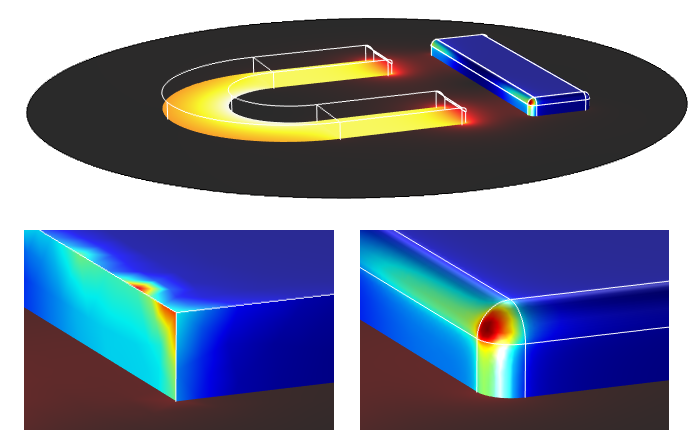
马蹄形磁铁周围的磁通密度和附近铁棒上的麦克斯韦应力张量分布。特写图显示了不带(左)和带(右)圆角的铁棒上的局部通量密度。
除了电磁学之外,许多其他解变量梯度(热通量、应力和应变等)也表现出相似的奇异性。如果对边缘和角进行倒圆角处理,结果将变得平滑。我们可以在有关奇异点的识别这篇博客文章中阅读更多内容。
重要说明
最后需要说明的,但并不是最不重要的一点是:不要切除边角!通过使用更简单的倒斜角操作而不是使用倒圆角来降低总网格数听起来可能很吸引人,但是,这会使边缘变成一个笔直的形状,而不是平滑的弯曲,并且虽然删除了一个奇异点但又引入了至少两个额外的奇异点。
从 5.0 版本开始,COMSOL Multiphysics®软件中已包含 2D 圆角(和斜角)。在 3D 模拟中,我们需要使用设计模块进行设置。



评论 (0)