借助拓扑优化找出结构的最优设计

想想第一批设计桥梁的建筑师们，他们肯定经历了许多次的尝试和失败，才做出了能让人们安全通过水面的设计。当然，如果当时有计算机的话，他们将能通过 COMSOL Multiphysics 和优化模块来极大地简化这一过程。讨论建筑及桥梁的优化之前，让我们先来探讨如何借助拓扑优化找出简支梁的最优设计。

简支梁示例

在我们的钢结构梁示例中，梁的两端安装有辊支撑，边载荷作用在梁中部的顶面上。梁尺寸为 6mx1mx0.5m。我们将在此示例中使用线弹性域，同时因为梁尺寸的关系，我们选择了二维平面应力公式。注意：在 x=3m 处存在一个对称轴。

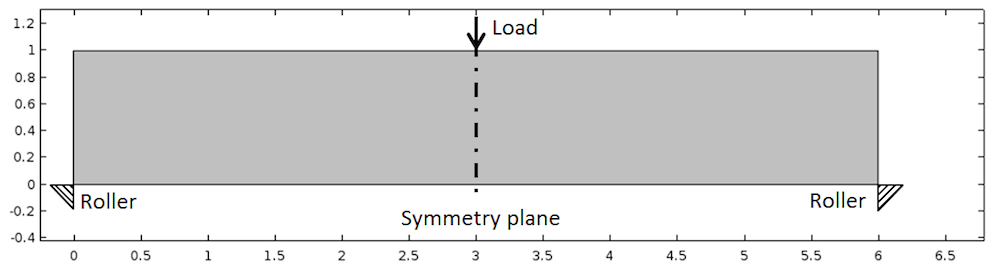
带有载荷及约束的梁几何。

通过正确的优化方法找出结构的最优设计

在上方的梁几何中，我们希望能在材料用量与梁刚度之间找出一个最佳的折中方案。为此，我们需要将它转化为数学语言以便进行优化计算。每个优化问题都涉及到找出最优的设计矢量 \alpha，以便最小化目标函数 F(\alpha)。从数学角度来看，这可以表示为 \displaystyle \min_{\alpha} F(\alpha)。

对设计矢量的选择决定了求解优化问题的类型：

• 如果 \alpha 是几何的一组控制参数（如长度或高度），这就是一个参数化优化问题。
• 如果 \alpha 控制了几何的外部曲线，这将是形状优化问题。
• 如果 \alpha 是确定几何内某点为空心或实心的函数，则是拓扑优化问题。

拓扑优化适合用于对不确定结构进行最优设计。一方面，此方法的灵活性要优于其他方法，因为它支持将任意形状输出作为结果。另一方面，结果并非总是直接可行。因此，拓扑优化常用在最初阶段，方便指导后续设计。

实际操作时，我们将人为定义一个密度函数 \rho_{design}(X) ，几何内各点处 X = \lbrace x,y \rbrace 的值介于 0 和 1 之间。在结构力学仿真中，会通过这一函数来构建罚杨氏模量：

其中 E_0 是真实杨氏模量。因此，\rho_{design}= 0 对应于空洞部分，\rho_{design}= 1 对应于实体部分。

如前所述，根据目标函数，我们希望最大化梁的刚度。在结构力学问题中，最大化刚度等同于最小化柔度。从能量的角度来说，它还相当于最小化总应变能，后者的定义为：

因此我们的拓扑优化问题可以写作：

在 COMSOL Multiphysics 中进行拓扑优化

既然已经定义了优化问题，我们现在可以在 COMSOL Multiphysics 中进行设定。本篇博客将不会展开介绍仿真中的固体力学部分。不过，我们的几个结构力学模块教程模型可以帮助您理解怎样在 COMSOL 中进行固体力学的建模。

增加优化物理场接口后，就可以在求解域中定义一个控制变量场。当对 \rho_{design} 进行首次离散时，我们可以选择一个常数单元阶次，意思是 \rho_{design} 在所有网格单元中的值保持唯一。

这一步完成后，可以针对结构力学仿真定义一个新的杨氏模量，例如 E(X)=\rho_{design} E_0。

如前所述，对目标函数在整个域内进行积分。在优化接口选择积分目标。弹性应变能密度即为预定义变量 solid.Ws。因此，目标函数可以轻松定义为 \int_\Omega Ws \ d\Omega。

我们今天讨论的重点并非优化的实际工作原理。基本上，优化求解器会从初始猜测值开始，然后对设计矢量进行迭代，直到目标函数达到最小值。

如果运行该优化问题，将得到如下结果。

初始测试结果。

仅仅为了达到最大化刚度的目标，该结果的意义不大，因为它显示所有计算区域都被原始材料填充！

经过初始测试后，我们总结出，如希望通过优化算法来选择一项设计，应使用质量约束。当将约束设为 50% 时，我们可以将它写作：

在 COMSOL Multiphysics 中，可以通过增加 积分不等式约束引入质量约束。此外，\rho_{design} 的初始值需要设为 0.5，以便在初始态时满足这一约束。

下方动画显示了这一新问题的优化结果。

增加质量约束后的结果。

虽然这次的结果要好一些，但仍然存在一个问题：\rho_{design} 中很多区域的值为中值。对该项设计而言，我们只需了解指定区域是否为空心。为了尽量使 \rho_{design} 内的值为 1 或 0，应对中间值进行罚处理。为此，我们需要在罚杨氏模量表达式中增加指数 p：

事实上，将 p 取值在 3 到 5 之间。例如，如果 p = 5 且 \rho_{design}= 0.5，罚杨氏模量将为 0.03125 E_0。同时，对质量约束的贡献仍为 0.5。因此，优化算法会尝试控制设计矢量为 0 或 1。

使用新的罚杨氏模量，我们得到如下结果：

使用新的罚杨氏模量得到的结果。

我们新的梁设计开始成形了！但该设计表现为一个有问题的棋盘式设计，因为高度依赖于选择的网格。为了避免出现棋盘设计，我们需要控制 \rho_{design} 在空间中的变化。为了计算变量场的变化，方法之一是在整个域中求它的导数模的积分：

一个新问题出现了：我们如何才能同时最小化 \rho_{design} 的变化以及总应变能？

由于还需要一个标量目标函数，因此必须综合考虑这些目标。我们可以考虑增加这些目标，但首先应对这两个表达式进行比例缩放，使其值接近 1。考虑到刚度目标，我们只需用 Ws0 去除，即 \rho_{design} 为常数时的总应变能。对于正则化项，我们可以取以下比例因子 \frac{h_0 h_{max}}{A}，其中 h_{max} 是最大网格尺寸、h_0 是解的预期尺寸，A 是设计空间的面积。我们的最终优化问题现在可以写作：

其中 q 因子控制了正则化权重。

最后，需要将 \rho_{design} 的离散改为 Lagrange 线性单元，以便计算它的导数。

通过求解最终问题得到的结果能帮助我们深入了解梁的最优结构设计。

正则化结果。

在现实生活中，我们可以看到不同尺度的此类设计，如下方的桥梁所示。

华伦桁架桥。公共领域图片，通过 Wikimedia Commons 分享。

在水面上设计一座桥

现在我们已经确定了拓扑优化方法，接下来将讨论一个更复杂的设计空间。我们希望回答这一问题：如何在水面上设计一座桥。为了实现这一点，必须在几何中定义一个载荷区域，在该区域中杨氏模量没有被罚函数化。

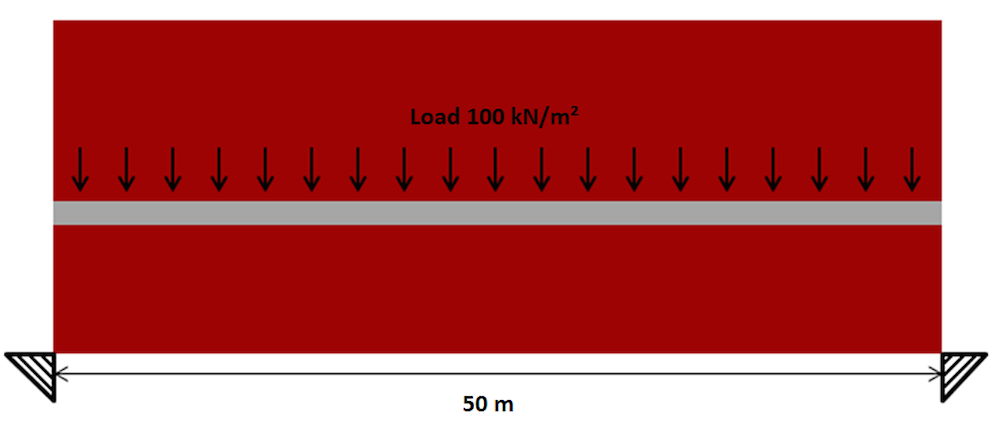
拱桥的设计空间。

经过几次迭代后，我们可以得到一个非常好的拱桥设计，也是一个令人印象深刻的设计。结果可以帮助建筑师更深刻地理解桥梁将采用的设计。

拱桥的拓扑优化结果。

虽然无法通过数学优化算法得出具体的设计方案，但上图中的结果可以帮设计师设计出真正的桥梁设计。下方的巴约纳大桥就是这样一个例子。

巴约纳大桥。公开领域图片，通过 Wikimedia Commons 分享。

有一点很重要，您可以按照同样的步骤将拓扑优化方法用于三维案例。对于类似的桥梁设计问题，我们可以在下方的动画中看到对上承式拱桥设计的三维测试。

上承式拱桥拱桥的三维拓扑优化。

结束语

博客介绍了在结构力学分析中使用拓扑优化方法的基础知识。如您希望自己操作这一方法，那可以在 App 库中下载我们的MBB 梁的拓扑优化教程。

虽然拓扑优化方法最初针对机械设计开发，但罚方法同样可以用于 COMSOL Multiphysics 中各类基于物理场的分析。例如，最小化微通道中的流速教程就为我们提供了一个流动优化示例。

参考文献

1. “Optimal shape design as a material distribution problem”, by M.P. Bendsøe.
2. Topology Optimization: Theory, Methods, and Applications, by M.P. Bendsøe and O. Sigmund.