
本文是关于结构动力学阻尼的博客文章的续篇,这里我们将详细讨论带阻尼的机械系统的谐波响应,在 COMSOL Multiphysics® 软件中演示设置频率响应分析的不同方法,以及如何解释结果。
什么是频率响应?
一般而言,系统的频率响应显示系统的某些属性对以频率形式输入的激励产生响应的函数。COMSOL Multiphysics中的频率响应,通常是指对谐波激励的线性(或线性化)响应。为了生成频率响应曲线,需要进行频率扫描; 也就是对很多不同频率进行求解。通常,频率响应曲线将表现出许多与系统固有频率对应的不同峰值。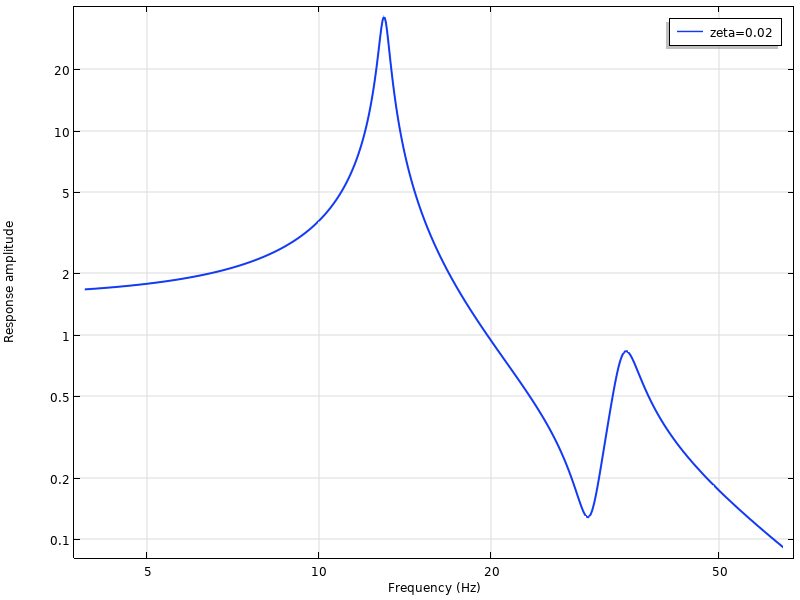
典型的频率响应曲线。绘制范围内有两个固有频率,分别为13 Hz和31 Hz。
重新审视单自由度系统
在之前的博客文章中,我们讨论了具有黏性阻尼的单自由度系统动力学的各个方面。其中阻尼的固有频率为
\omega_d = \omega_0\sqrt{1-\zeta^2} \approx \omega_0 \left ( 1 – \frac{\zeta^2}{2} \right )
该频率是指在没有其他外部激励的情况下,将系统从变形状态释放之后,产生振动(具有衰减幅度)的频率。此时,一个有趣的问题出现了:“哪个激励频率会给出最大幅度的响应?”一般会认为恰好是阻尼的固有频率,但如下图所示,情况并非如此。
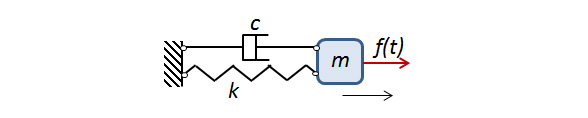
单自由度系统。
由于系统是谐波运动,因此采用复数表示法。分解出常见的谐波乘数e^{i \omega t},可得运动方程为
\left (-\omega^2m +ic\omega +k \right) u = f
载荷f的相位角可以作为参考,因此f是实值。除以刚度k可以得到归一化形式:
\left (1-\left (\frac{\omega}{\omega_0} \right) ^2 +2i\zeta \left (\frac{\omega}{\omega_0} \right) \right) u = \frac{f}{k}
等式的右边是静态位移。因此,动态解和静态解之比是
\displaystyle H(\omega) = \left (1-\left (\frac{\omega}{\omega_0} \right) ^2 +2i\zeta \left (\frac{\omega}{\omega_0} \right) \right)^{-1} =\frac{1}{1-\beta ^2 +2i\zeta \beta}
H 函数通常称作传递函数。其中 β 表示激励频率与无阻尼固有频率的比值。传递函数的大小为。
在此,β 用来表示激励频率与无阻尼固有频率之间的比率。 传递函数的大小为
\displaystyle \left | \frac{1}{1-\beta ^2 +2i\zeta \beta} \right | = \frac{1}{\sqrt {(1-\beta ^2)^2 +4\zeta^2 \beta^2}}
下图显示了此功能。
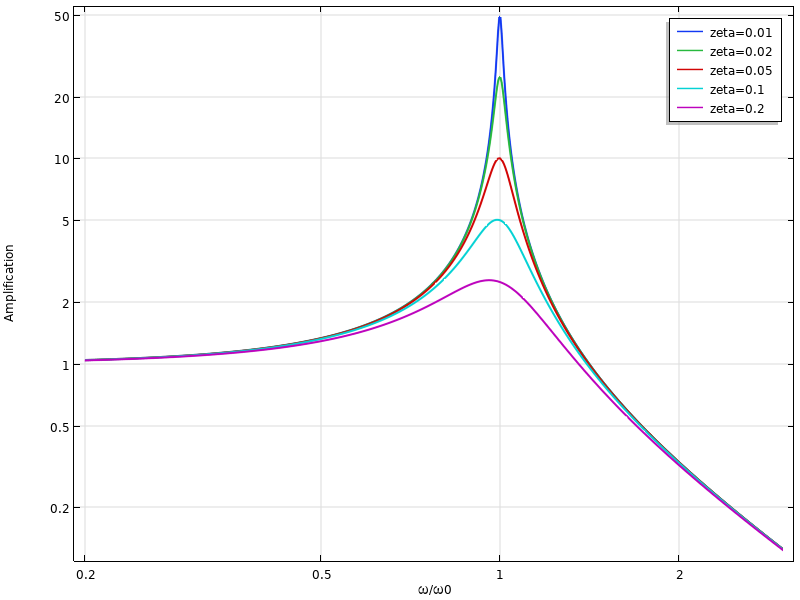
使用标准微积分,可以通过找到(平方)分母的最小值来确定给出最大振幅的频率{(1-\beta ^2)^2 +4\zeta^2 \beta^2}为
\beta = \sqrt{1-2 \zeta^2}
因此,给出最大响应的激励频率为
\omega_{\mathrm {max}} = \omega_0\sqrt{1-2\zeta^2} \approx \omega_0 \left ( 1 – \zeta^2 \right )
最大响应的激励频率低于阻尼固有频率, 实际上,频移接近两倍。
最大响应的激励频率与自由频率不同,这似乎是矛盾的,但可以解释为由阻尼引起的力与位移之间的相移所导致。在无阻尼的情况下,载荷和位移在低于固有频率时完全同相,高于固有频率时翻转到180°异相。而有了阻尼之后,相移是平滑过渡,如下图所示。无论阻尼水平如何,无阻尼固有频率的相移始终为 90°。
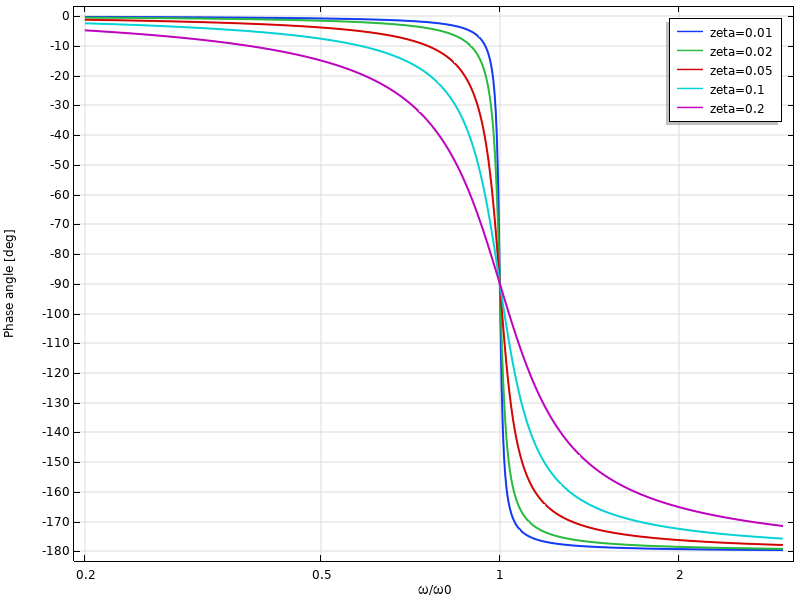
位移的相移作为频率的函数关系。
当存在阻尼时,由于力可能向系统提供能量,因此造成力和位移产生相移。
损耗因子的阻尼
对具有阻尼损耗因子的单自由度系统进行分析,此时系统的运动方程为
\left (-\omega^2m +k(1+i\eta ) \right) u = f
阻尼的固有频率为
\displaystyle \omega_d = \omega_0 \sqrt {\left( \frac{1}{2}
\left( 1 + \sqrt{1+\eta^2} \right ) \right ) } \approx \omega_0 \left (1 + \frac{\eta^2}
{8} \right )
令人惊讶的是,增加阻尼并不会使固有频率减小,而是增加。这是因为这种形式的损耗因子阻尼实际上会增加刚度。复数刚度的绝对值是
|\tilde k| = k \sqrt {1 + \eta^2} \approx k \left ( 1+ \frac{\eta^2}{2} \right )
由于这种损耗因子阻尼,传递函数为
\displaystyle \frac{1}{1-\beta ^2 +i\eta }
其大小为
\displaystyle \left | \frac{1}{1-\beta ^2 +i\eta} \right | = \frac{1}{\sqrt {(1-\beta ^2)^2 +\eta^2}}
可以看出,当β= 1时(即,无阻尼固有频率),振幅最大。同样,最大响应频率低于有阻尼时的固有频率。
前一篇博客文章中提到,损耗因子阻尼的另一种定义具有如下属性:复数刚度的绝对值与阻尼水平无关具有以下属性:复杂刚度的绝对值与阻尼水平无关。这可以使用对复数刚度进行归一化的定义方法来获得如下复平面的纯旋转。
\tilde k = \displaystyle \frac{k(1+i \eta)}{\sqrt{1+ \eta^2}}
由上述公式可知,固有频率随着阻尼而减小:
\displaystyle \omega_d = \omega_0 \sqrt { \frac {\frac{1}{2} \left( 1 + \sqrt{1+\eta^2} \right )}{1+ \eta^2} } \approx \omega_0 \left (1 – \frac{3\eta^2}{8}
\right )
本文不做详细分析,结论是相应的激励频率下降,将给出最大振幅,因此仍低于有阻尼的固有频率。
当考虑损耗因子阻尼时,激励和响应之间的相移非常有趣:即使在非常低的激励频率下,相移仍然存在,且其渐近于arctan(η)。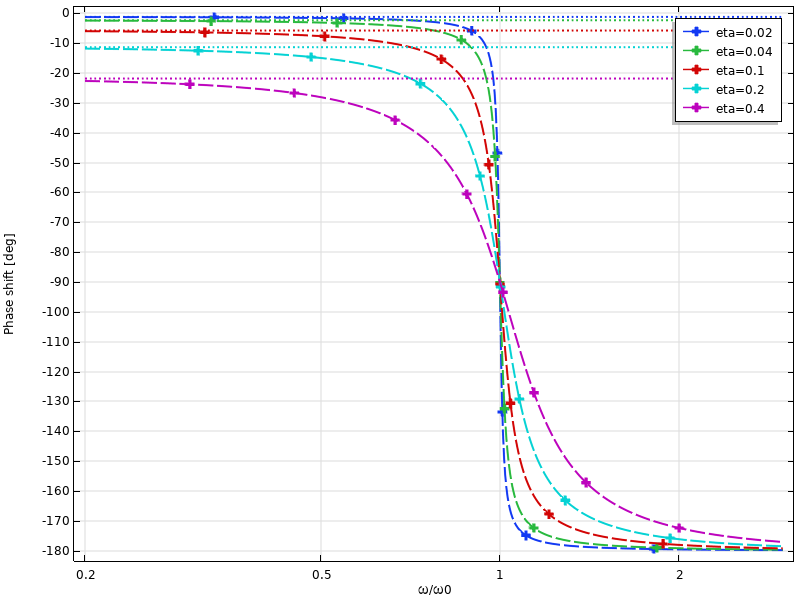
当使用损耗因子阻尼时,位移的相移与频率的函数关系。低频渐近线用虚线表示。
考虑摩擦因素
当两个表面之间的摩擦提供阻尼机制时,由于系统的非线性,对谐波输入的响应不再是谐波,可能仍然会存在周期性,但并不是谐波响应。频域法无法解决这些问题,因为其假设是输入输出为线性关系。
在 COMSOL Multiphysics® 中进行频率响应建模
建立研究
在模型向导中添加结构力学物理接口后,您将看到许多研究类型,其中四种可用于计算频率响应:
- 频域
- 频域,预应力
- 频域,模态
- 频域,预应力,模态

Solid Mechanics界面的可用学习类型。
其中两项研究使用直接求解方法,两种研究使用模式叠加方法。在预应力分析类型中,考虑了静止预载荷的刚度变化。模态叠加非常适合频域分析,因为它它能根据给定的频率选择合适的本征模。
在任何一种情况下,您都可以通过在研究设置中提供计算响应的频率列表来执行频率扫描。通常,您希望将频率聚集在结构的固有频率附近。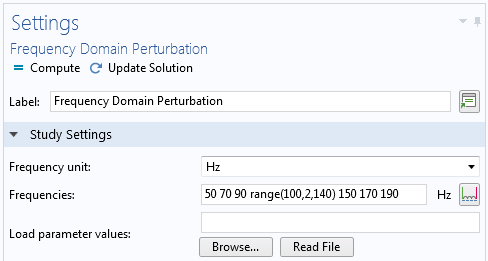
输入频率可进行频率扫描。
需要注意的是,如果阻尼为零,则在固有频率下的响应趋于无穷大。这意味着不可能在固有频率处或接近固有频率时解决无阻尼频率响应问题。数值公式将给出奇异或至少是病态的系统矩阵。
是否存在扰动?
对于频域研究,求解器序列中的稳态节点中有一个非常重要的设置,即线性。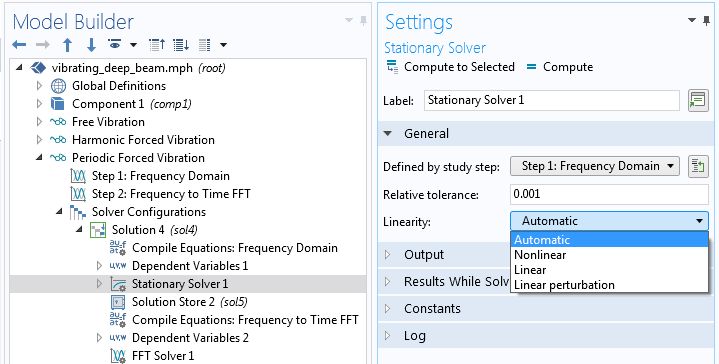
选择“线性” 属性。
理论上,任何频域分析都可以被认为是一个小扰动,因此使用线性扰动绝不是错误的。绝不会出错。然而,最常见的情况是振动以零为中心。在这种情况下,它并不真正关心问题是线性或线性扰动。但是,该设置从根本上改变了载荷方式。载荷可以标记为谐波扰动。如果将线性度设置为线性扰动,则仅考虑此类负载。 在研究中忽略所有未标记为谐波扰动的载荷。相反,如果是线性而不是线性扰动,则忽略标记为谐波扰动的所有载荷,并将其他载荷视为谐波。

边缘载荷,指定为谐波扰动。
该设置的目的是能够区分导致可能的预应力状态的负载和作用于其上的谐波激励。
添加标准频域研究时,默认情况下,研究不会设置为扰动。因此,在这种情况下,谐波扰动标签不应用于载荷,除非您更改线性度设置。当您添加频域,预应力研究时,频率响应研究步骤设置为扰动分析。如果研究是模式叠加类型,则研究始终是线性扰动。
解释结果
频域分析的结果是复值,其中隐含了谐波变化。复数的相位角描述了与参考相位之间的相移(可以任意选择,但通常作为主载荷的相位)。它还提供有关结构中不同点之间相移的信息。需要注意的是,由于单个有限元内的位移分量可以具有不同的相位角,因此应力张量的分量也很可能彼此不同相。这在疲劳分析中会比较重要。
在许多情况下,如在彩色图中,只能显示实数。所有展示的结果约定如下:如果期望查看一个复值变量v的实数值时,则使用实数部分。
\displaystyle v = \Re(\tilde v e^{i \phi})
其中,数据集的属性(如相角Φ)是可以修改的。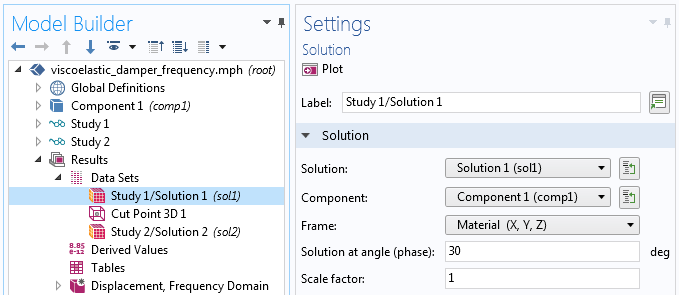
调整数据集中的相角。
在大多数频率响应分析中,通常关注的是结果的振幅v与频率的函数关系。因此应该研究abs(v)而不是v本身。两者之间的差异如下图所示。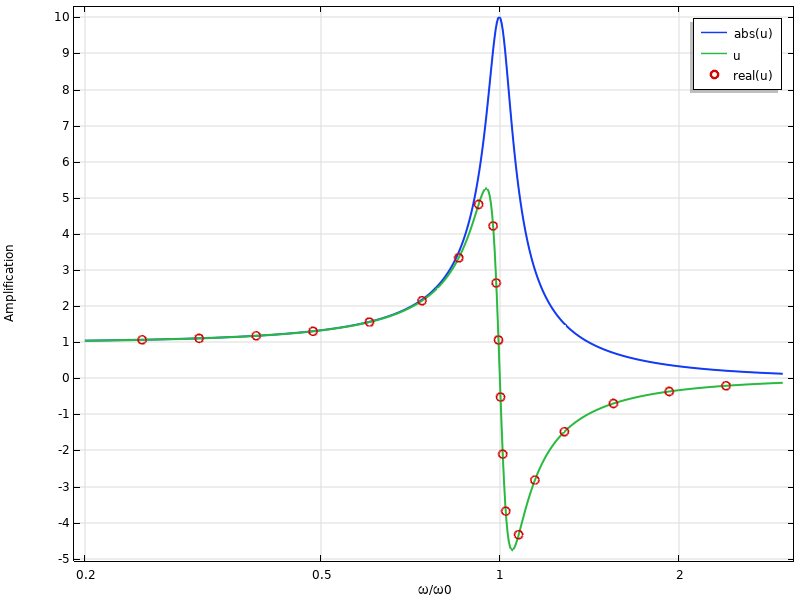
频率响应图的示例。注意,“u”的图形与“real(u)”相同。
为了更详细地了解发生的情况,我们可以将结果的虚部和辐角添加到图中: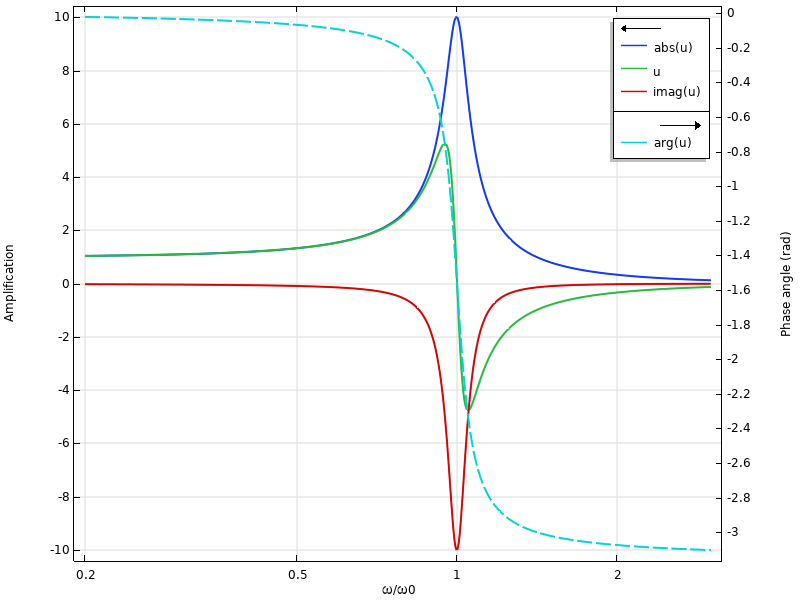
包括相移的频率响应。
在低频时,实部接近绝对值。在固有频率附近,则主要是虚部。这意味着响应与激励几乎不同相。考虑一下,如果将数据集里面的相角改为 45°,频率响应会怎样变化。
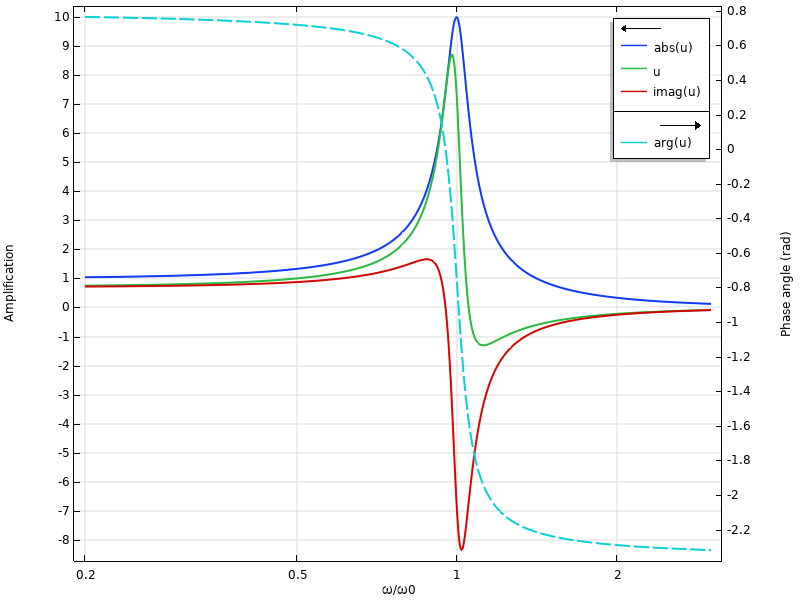
当数据集中的相位角为 45° 时的频率响应。
由上图可知,正如预期,振幅不会改变。但实部和虚部的各个值均会改变,其中相角曲线向上移动 π/4。实际上,如果向载荷添加45°相位角,我们将获得完全相同的结果图。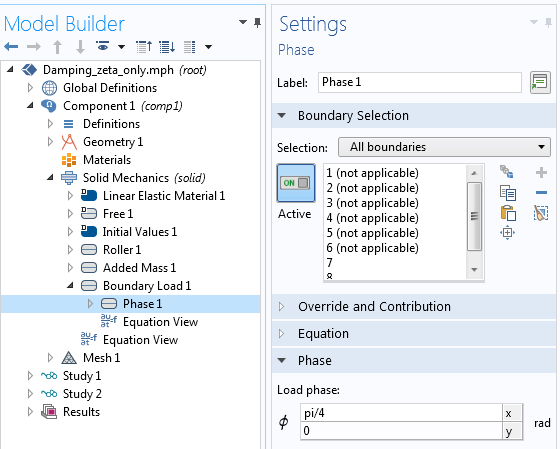
向载荷添加相位角。
在模型中,除了上述相角输入,您还可以使用复数表示法直接输入载荷: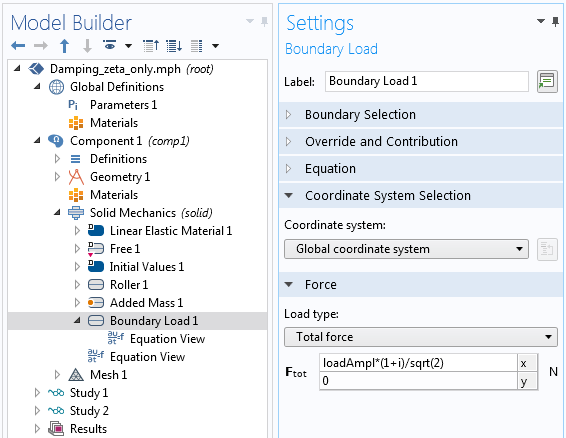
与上述相同载荷的复数表示法。
当所有载荷并非彼此同相时,能够规定相角非常重要。例如,可以通过使y方向上的载荷相对于x方向上的载荷具有 90° 相移,来方便地描述一个旋转的非平衡受力物体。
扰动研究的结果
如果研究是扰动类型,则会有两组结果:预应力解和扰动解。在这种情况下,可以在各种结果表示功能中访问额外的选择::待求表达式。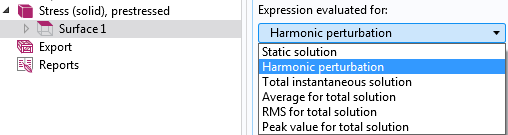
选择扰动分析的计算类型
在这里,您可以选择研究扰动解,预应力解或其组合。对于扰动解,您还可以获得一个选项:计算微分复选框。
选择计算微分。
此设置会影响非线性表达式的处理方式。如果未选择计算微分,则会在面值处获取非线性数量。例如,u^2将会很方便地从扰动解中获取变量u的平方。由于 u 通常是复值的,因此通常该操作是无意义的。
当选择计算微分时,则该非线性量将预应力状态附近线性化。表达式u^2将计算2*u0*u,其中u0是线性化点处的值。
将频率响应结果转换为时域
在某些情况下,您可能希望在时域中进行频域分析的谐波响应可视化,尤其希望有多个激励频率。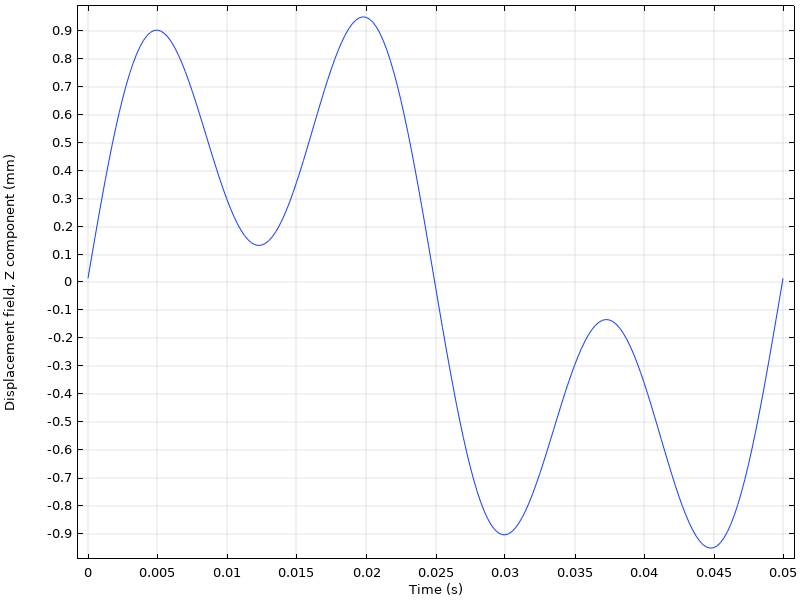
受到两个不同频率载荷激励的响应。
您可以使用频域到时域 FFT研究步骤将频率响应结果转换到时域。
从频域到时域的转换结果研究序列。
此技术用于以下教程模型:
结束语
频域分析是分析受谐波激励的线性系统的有力工具。实际上,通过对负载进行初始傅里叶变换,可以使用频率响应分析来研究任何类型的周期性激励。
COMSOL 案例库中还有更多机械频率响应分析示例,例如:



评论 (2)
王 巍
2019-10-22很棒,谢谢
Xing Su
2021-11-08很棒,谢谢