变形固体中的传热仿真

在之前的文章中，我们介绍了一些涉及静止固体耦合传热的应用。这些静止固体传热示例对将要求解的传热方程进行了简化处理，并且通常可以得到求解温度场的精确近似。当涉及传热和固体力学的多物理场耦合时，如何描述用于解释材料热弹性效应的相关物理场？阅读今天的文章，了解更多内容。

材料和空间坐标系

在介绍物理场之前，我们先简要回顾一下 COMSOL Multiphysics 中使用的坐标系。当考虑几何非线性时，固体力学接口会区分材料坐标系和空间坐标系。材料坐标系以初始状态的坐标\mathbf{X}= (X, Y, Z)表示物理量，而空间坐标系以当前状态的坐标\mathbf{x}=(x, y, z)表示物理量。

下图展示了一个承受压缩应变的正方形几何示例。该正方形长 10cm，其左下角最初位于(X, Y) = (1~\textrm{cm}, 1~\textrm{cm})，之后其左右两侧受到边界载荷的压缩而发生变形。此变形会使正方形上几乎所有点的位置发生改变。例如，左下角移至新的位置(x, y) = (1.54~\textrm{cm},0.82~\textrm{cm})。

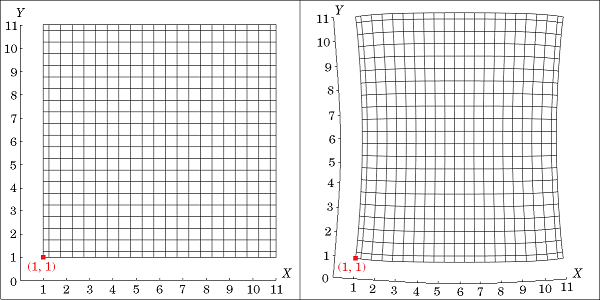
用材料坐标表示的变形的正方形，左侧为初始状态，右侧为最终状态。

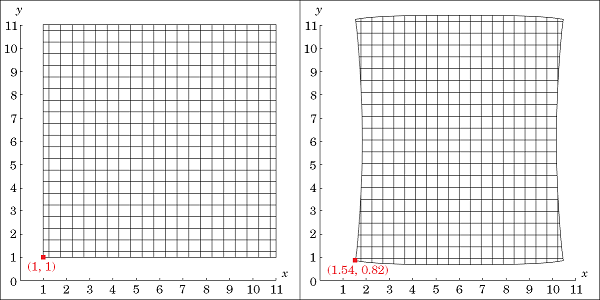
用空间坐标表示的变形的正方形，左侧为初始状态，右侧为最终状态。

材料坐标始终指时间上的同一质点，它最初位于指定点(X, Y, Z)。固体力学的动量方程在此坐标系中建立。另一方面，空间坐标系中的点(x, y, z)是指当前状态下可能位于该点的任何质点，热方程在该坐标系中建立。

在这两个坐标系中，与体积相关的物理量具有不同的值。例如，在没有任何质量源的情况下，材料坐标的密度在变换之前和之后保持恒定，而空间坐标的密度随体积变化而变化。因此，为了将在材料坐标（结构力学）上建立的方程和在空间坐标（传热）上的建立另一个方程耦合起来，需要在每个坐标上合理评估这些值。下表列出了一些从材料坐标到空间坐标的热物理量转换。这些转换涉及变形梯度\mathbf{F} = {\partial \mathbf{x}} /{\partial \mathbf{X}}及其行列式J。二者均使用由固体力学接口计算的位移场评估。

物理量	材料坐标	空间坐标
温度	T	T
密度	\rho_0	\rho = J^{-1} \rho_0
导热系数张量	\bold{k}_0	\mathbf{k} = J^{-1} \mathbf{F}\mathbf{k}_0 \mathbf{F}^T
热弹性阻尼	W_{\sigma, 0} = \boldsymbol{\alpha} T :\frac{\mathrm{d} \mathbf{S}}{\mathrm{d} t}	W_\sigma = J^{-1} W_{\sigma, 0}
热源	Q_0	Q = J^{-1} Q_0

从材料坐标到空间坐标的热物理量转换。

这些转换还反映了一个事实，即应力和应变会通过修改几何结构（如空间坐标所示）影响传热。例如，延伸的边界更可能接收更多辐射热量（Q_\mathrm{r} > Q_{\mathrm{r}, 0}）， 如下图所示。

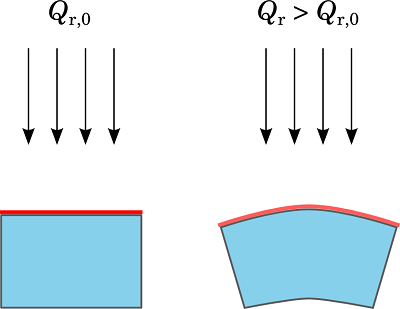
固体上表面接到的辐射热通量，初始状态（左）和拉伸上表面后（右）。

另一个示例是空间坐标中的导热系数表达式，通常使用初始状态值\bold{k}_0，以及和固体应变有关的数量\mathbf{F}和J。

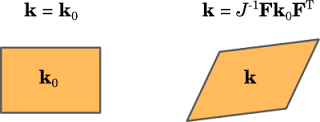
固体变形后，空间坐标上导热系数的变化。

与温度相关的应力和应变

固体力学方程是在材料坐标中定义的。通过线性动量平衡方程和应力-应变关系将位移\mathbf{u}、第二类皮奥拉-基尔霍夫应力张量（second Piola-Kirchhoff stress tensor）\mathbf{S}，以及弹性应变张量（elastic strain tensor）\mathbf{E}_\mathrm{el}相关联。

(1)

(2)

其中，\mathbf{C}是弹性张量，通常由杨氏模量和泊松系数定义。对于碳素结构钢 1020，该量可能与温度有关。

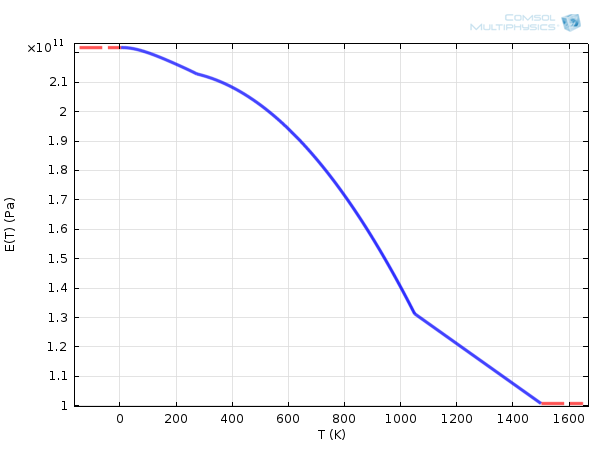
碳素钢结构 1020 的杨氏模量与温度有关。

下列公式说明，在没有任何塑性效应的情况下，弹性应变张量\mathbf{E}_\mathrm{el}通过热应变张量\mathbf{E}_\mathrm{th}传递温度相关性：

(3)

(4)

(5)

热膨胀系数\boldsymbol{\alpha}，表征材料由于温度变化而收缩和膨胀的能力。通常是标量，但可能更常采用张量的形式。下表列出了各向同性\boldsymbol{\alpha}的一些典型值。

材料	热膨胀系数（10-6K-1）
丙烯酸塑料	70
铝	23
铜	17
尼龙	280
石英玻璃	0.55
结构钢	12.3

一些材料的热膨胀系数。

此外，\boldsymbol{\alpha}本身也与温度相关，如下例所示。

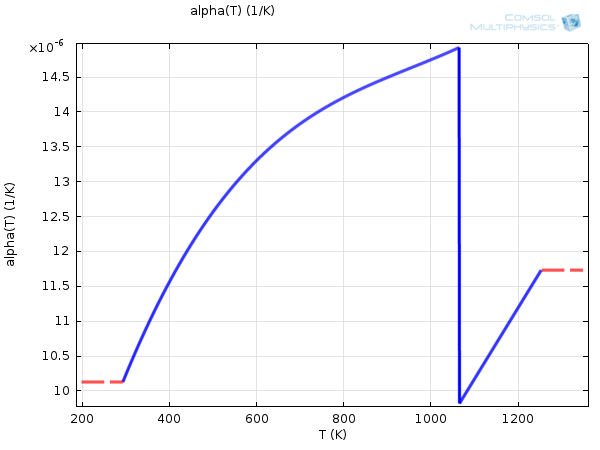
碳素结构钢 1020 的热膨胀系数，与温度相关。

从这些示例中可以看出，\boldsymbol{\alpha}的值通常在 10^-5K^-1数量级。因此，为了使\mathbf{E}_\mathrm{th}变得显著，必须与参考温度有较高的温差。例如，铝需要达到高于参考温度约 500K 才具有 1.2％ 的热伸长率。

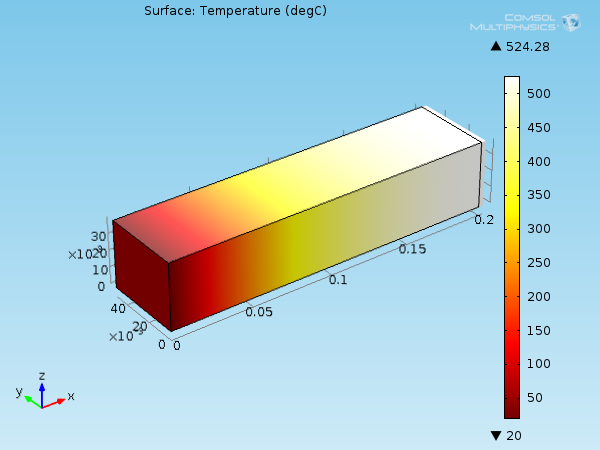
加热至 500K 的受约束的铝制横梁的热膨胀示例，采用 1:1 变形比例。

注意，在等式（3）-（5）的公式中，热应变是从总应变中减去的。由于热应变的值通常较小，因此对于小应变（通常为热应变）来说，这是一个合理的近似。适用于较大热应变的更精确的乘法公式如下所示，后文不再讨论。COMSOL Multiphysics 中的超弹性材料中采用的就是这种计算方法。

(6)

(7)

(8)

变形固体的热方程

热方程是由热力学第一定律推导出的能量平衡方程。对于固体，在空间坐标上采用以下形式：

(9)

耦合项W_\sigma是由于固体压缩或膨胀而产生的热源，其定义为：

(10)

式中，由于\boldsymbol{\alpha}与温度无关，可以简化为：

(11)

式中\boldsymbol{\alpha}是和\mathbf{E}_\mathrm{th}表达式一样的热膨胀系数。如上表所示，低的\boldsymbol{\alpha}值必须通过足够高的T {\mathrm{d} \mathbf{S}} / {\mathrm{d}t}值作为补偿，以使W_\sigma成为重要的热源，即：

• 在高温下
• 通过快速和高度变化的应力

下列为描述传热与固体力学多物理场耦合的 4 个关键贡献：

1. 应变和应力对材料或空间坐标中的热量和边界热通量的影响
2. 与温度相关的弹性矩阵
3. 通过热应变张量与温度相关的弹性应变张量
4. 热源W_\sigma，对应于固体中的热弹性阻尼

接下来，我们将解释最后 2 个耦合贡献，并将通过几个仿真示例来展示如何在 COMSOL Multiphysics 中处理它们。

示例 1：涡轮静叶片中的热应力

我们之前的博客中曾详细地描述了如何模拟涡轮静叶片中的热应力。在这里，为了显示J_\mathrm{th}的影响，我们只展示了结果。因为这是一个稳态模型，所以可以忽略热弹性阻尼W_\sigma。

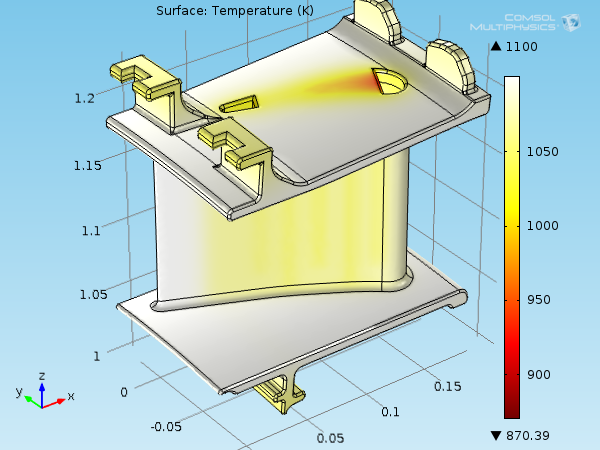
在材料坐标中表示的叶片表面温度场。

由于处于高温环境，与最初静叶片形状的参考温度 300K 相比，温度场的值介于 870K 和 1100K 之间。如此高的温度更容易使材料发生热变形。平均热膨胀系数和温度约为 1.2·10^-5K^-1和 1070K，\mathbf{E}_\mathrm{th}在 0.9％ 左右。

对于大变形，热效应导致的体积膨胀为\Delta V/V_0 = J_\mathrm{th}-1（J_\mathrm{th}
在等式（8）中被引入）。对于小应变，它仍然是一个很好的近似值，约产生 2.80％ 的膨胀。在结果与可视化中，实际的体积膨胀为 2.76％。

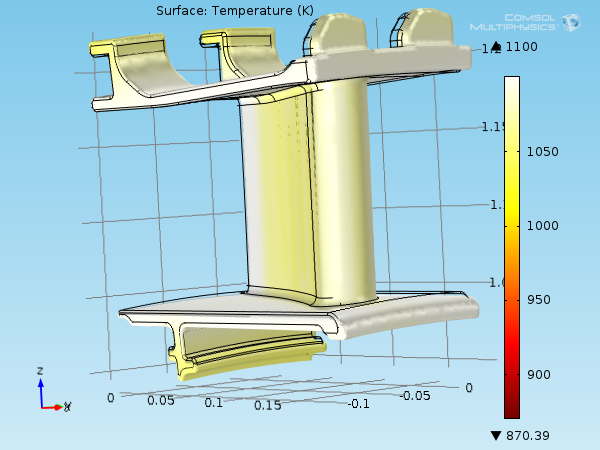
静叶片的温度场和变形，为了提高可见性，将绘图放大了 3 倍。

示例2：支架传热的瞬态分析

结构力学模块的模型库和 COMSOL 案例库中都提供了支架瞬态分析模型。在这个模型中，支架臂随快速瞬态载荷移动，温度将发生微小的变化。

现有模型忽略了这些热效应，因此，我们需要在固体传热接口中增加新的传热。

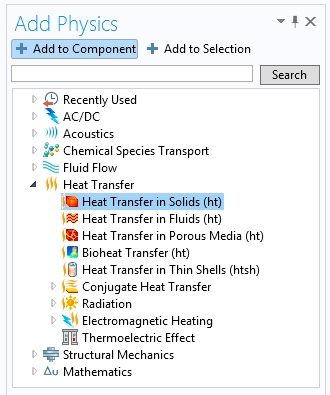
然后，添加以下两个多物理场特征，将固体传热和固体力学接口耦合起来：

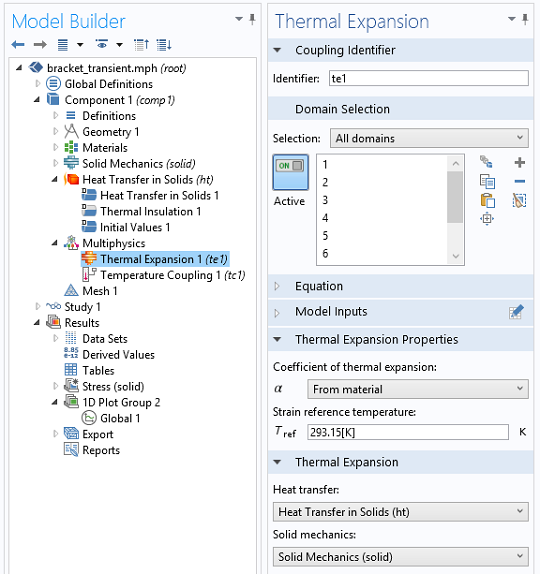
• 热膨胀
  • 用于修正施加在整个支架域上的热应变张量\mathbf{E}_\mathrm{th}和热弹性热源W_\sigma
• 温度耦合
  • 用于将通过固体传热接口和固体力学接口计算出的温度变量耦合在一起

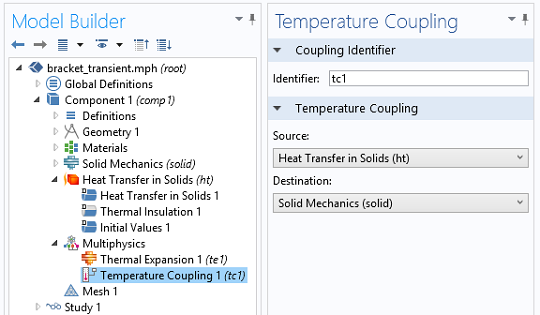
该研究还可以扩展到 30ms，以观察更多的载荷周期。

从各处的温度均为 20°C 等温剖面开始，微小的温度变化导致的热应变张量可忽略。现在，对热效应的主要贡献为由快速应力变化引起的热弹性热源。

随时间变化的支架温度分布，为了提高可见度，将绘图放大了 10 倍。

在支架的极端温度之间可以观察到约 0.8K 的差异。与预期相符，加热和冷却过程位于应力更重要且应力变化更大的拐角处。

通过求解热方程和动量平衡方程，变形固体中的热量传递可以通过数值计算得出。根据实际情况，对两个坐标系加以区分：

1. 建立运动方程的材料坐标
2. 建立热方程的空间坐标

两个坐标中与体积有关的数量具有不同的值，并且需要相互转换，特别是对于特定的能量和密度。

这两个控制方程均包含耦合项，用于使固体运动与温度相关，传热与固体变形有关。如前文中的两个示例所示，COMSOL Multiphysics 中提供了可以描述这些过程的合适的功能。

当温度保持在参考温度附近并且应力没有太快变化时，这些耦合效应可以忽略不计。否则，应将它们添加到模型的公式中。

如果要深入研究该主题，您可以下载文中提到的模型相关文件，并通过下面的链接阅读相关的博客。

更多资源

• 模型下载：
  • 涡轮静叶片的热应力分析
  • 支架教程模型
• 之前的博客文章：
  • 共轭传热
  • 模拟涡轮静叶片中的热应力

编者注：为了与 COMSOL Multiphysics 5.1 版本保持一致，此博客已于 2015 年 7 月 23 日更新。