最近,人们对网络上一个很有趣的视频产生了很多争议。这个视频试图解释一个关于电的重大误解:电子在电路中携带能量。虽然该视频以及许多回应视频对此进行了精彩的讲解,但仍有许多值得我们继续探讨的东西。COMSOL Multiphysics®软件是一个对此进行研究的绝佳工具,接下来,让我们了解更多详细内容。
争议的背景
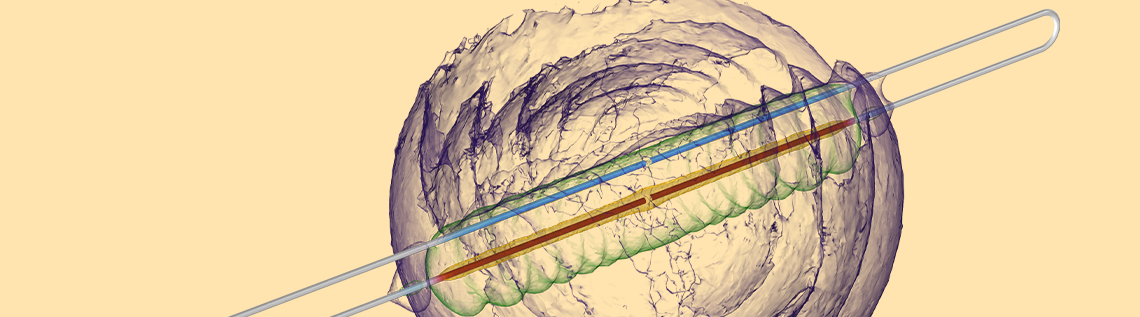
这一切都是因 “The Big Misconception About Electricity” 这个视频引起的。视频中给了一个类似于下图所示的电路图,有一个理想的电池通过一个理想的开关连接,形成一个理想的源。这个理想源由两根零电阻的电线连接,每根电线的长度为 30 万公里并沿相反的方向延伸,然后与一个放置在1米外的灯泡相连,形成环形回路。虽然视频中没有明确说明,但它假设整个电路位于某种空旷的宇宙中,没有被这个装置检测到的宇宙背景辐射。
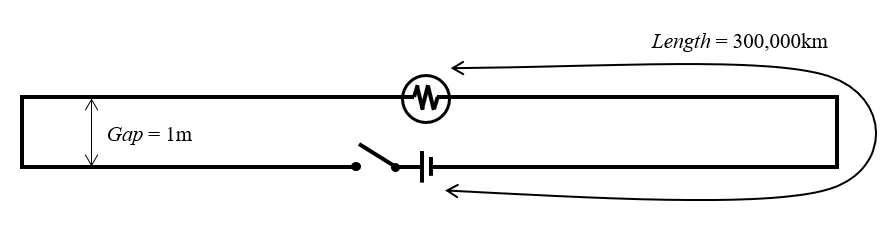
有争议的电路图。
问题:关闭开关时,信号从源传播到灯泡需要多长时间?正确的答案是 3.33 (ns)(Gap/c \approx 3.33\text{ ns},c是光速)。有许多视频提供了理解这个烧脑问题的不同方法。
也有人指出,我们应该定义一个阈值电流,并询问灯泡将在多大的电流下开启。这正是 COMSOL Multiphysics 擅长解决的实际问题,所以让我们直接开始建模吧!
建立数值模型并理解结果
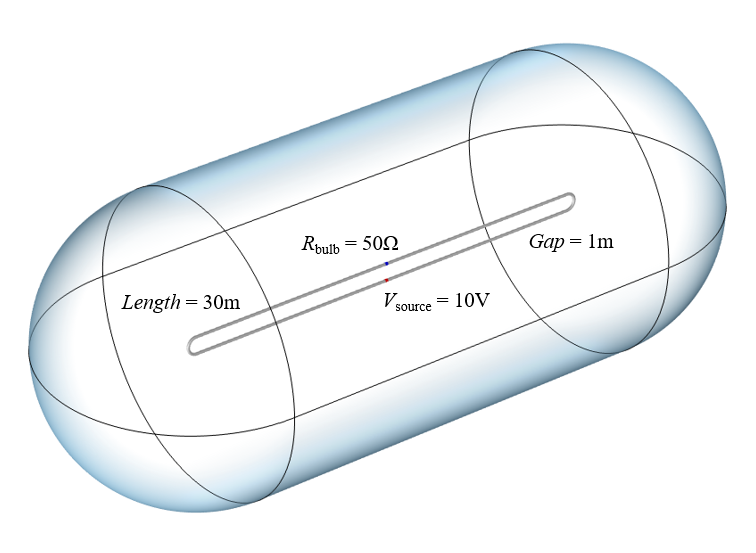
我们的计算模型。导线半径为0.1米,计算域半径为10米。
由于我们需要求解的是导线周围空间的电磁场,构建一个30万公里长的计算模型可能不太切合实际,但我们可以通过上图显示的小模型学到很多知识。为了对源进行建模,我们使用了 COMSOL®软件中的集总端口特征,从零时刻开始施加均匀电位。灯泡被建模为集总元件,在导线之间的间隙上增加了一个电阻。使用完美电导体边界条件对两根 30 米长的导线建模。假设导线是完美的导体是合理的,因为这种超导线已经可以制造出来了。电线周围的空间体积被视为理想真空条件,其边界被视为开放的自由空间。只要建立了这个计算模型,就可以求解和可视化电线上的场和电流。
结果显示了半透明等值面的电磁能量密度和沿导线的电流。部分信号以光速向外传播,在间隙另一侧的导线上感应出电流。场也由电线引导,并且存在辐射损失。随着时间的推移,整个电路的行为由系统的电感和电阻支配。
上面的动画显示了随时间变化的电路内部和周围的电磁能量密度。我们可以观察到,初始信号以光速向外传播,当时变场到达灯泡旁边的导线时,就会开始在灯泡中感应出电流。时变场主要由导线引导,但也有一些辐射,特别是在弯曲处发生反射。在最初的几百纳秒之后,场开始变得更加均匀。我们还可以绘制通过灯泡的电流随时间变化的曲线,并讨论它的形状传达给我们的有关系统的信息。
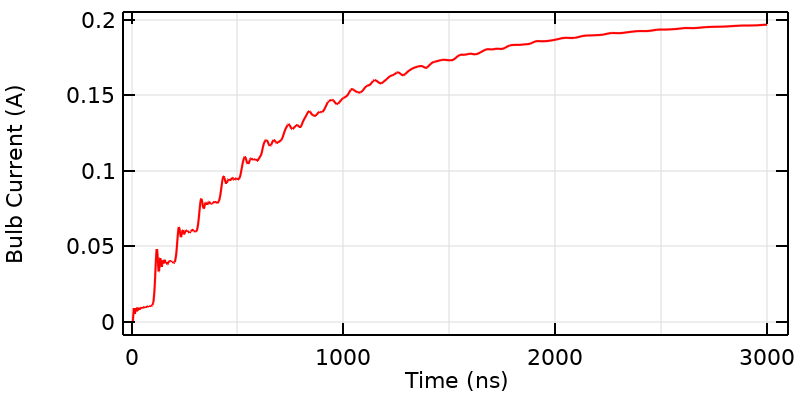
灯泡电流的时间比信号在间隙中传播的时间要长;它类似于RL电路的响应。
曲线的整体形状
如果查看曲线的整体形状,会发现似乎灯泡电流正在向稳态电流上升。这是因为这里实际上是一个 RL 电路,我们可以用以下等式描述曲线的整体形状(3.33 ns 之后):I\left( t \right) = I_{DC}\left( 1 – exp(-t/\tau_{RL})\right),其中 RL 时间常数为\tau_{RL} = L_{wires}/R_{bulb},电感L_{wires}可以通过一个稳态模型计算。总电感与导线的长度成正比,因此较长的环路将具有较慢的上升时间。
如果我们将灯泡打开时的阈值电流定义为I_{DC}
=V_{battery}/R_{bulb},那么(从严格的数学角度来看)电流只会无限接近I_{DC},理论上灯泡永远不会点亮。实际上,灯泡最终会被点亮,因为它实际测量的是离散数量的移动电荷的速度和加速度。但是,非常接近直流电流的阈值电流将意味着灯泡要到远大于 RL 时间常数的时间才会被点亮。
曲线中明显的平台
如果我们仔细地观察开始时间附近的曲线,会看到信号有几个明显的平台,产生一种阶梯形状。每个平台的特征时间为 100 ns,因为所施加的阶跃信号沿整条导线传播,并且恰好在每条导线的中点弯曲处发生一些反射。这些平台的高度与间隙的电容和电感耦合有关。
事实上,我们可以用传输线的电路模型来表征这种阶梯行为。请注意,这些平台会随着时间的推移而变得平滑,我们将很快找到这种平滑的来源。现在,我们来看第二种可能性:根据我们指定的阈值电流,灯泡可能会在 100ns 的整数倍时间点亮。
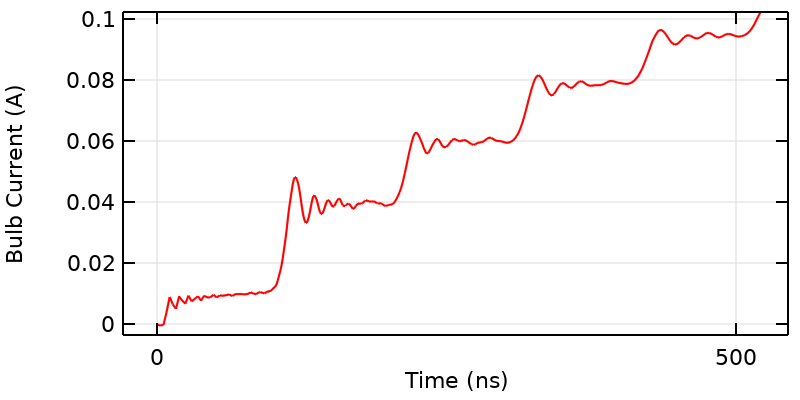
在初始时间附近,电流随时间也表现出明显的平台期,其周期等于信号沿整条导线传播的时间。此外,由于理想化开关的阶跃变化以及系统的谐振行为,还会产生振荡。由于系统中的损耗,这些会随着时间的推移而衰减。
快速的纹波及其衰减
如果我们更仔细地观察,会发现每一步的开始电流中都有明显的纹波,最初会出现较高的峰值,然后逐渐消失。这意味着如果我们选择合适的阈值电流,灯泡会先闪烁然后再亮,给出我们第三种可能!
这些纹波是由于系统的空间分布电容和电感造成的,这将导致无限数量的谐振,而不仅是一个。我们观测到的是系统被源激发的高阶谐振模式。但是,请注意,这些纹波似乎正在衰减,这种衰减和平滑是由于损耗造成的。损耗的来源之一是已知灯泡的电阻,它将存储在电池中的能量转换为热量和光。第二个损耗来源是由于电路的其他部分的能量辐射。正确预测这种损失需要我们在上文中构建的这种三维模型。
高频短波长的信号将比低频信号更快地辐射出去。另一种说法是较高的谐振具有较低的质量系数,或者导线是一种有损低通滤波器。
我们还应该问,如何将激发这些共振的高频信号信息引入模型。回想一下,当我们关闭开关时,会在施加的电势中引入一个阶跃变化。我们必须问自己这个步骤变化包含哪些频率信号?这个问题可以通过傅里叶变换来回答。事实上,我们的输入信号中有无限的频率,其中非常高频的信号的幅值很小,辐射相当快。另外值得注意的是,这个频率谱告诉我们有关电路及其设计的一些信息。如果我们改变导线中间弯曲的形状,会得到不同的反射信号。
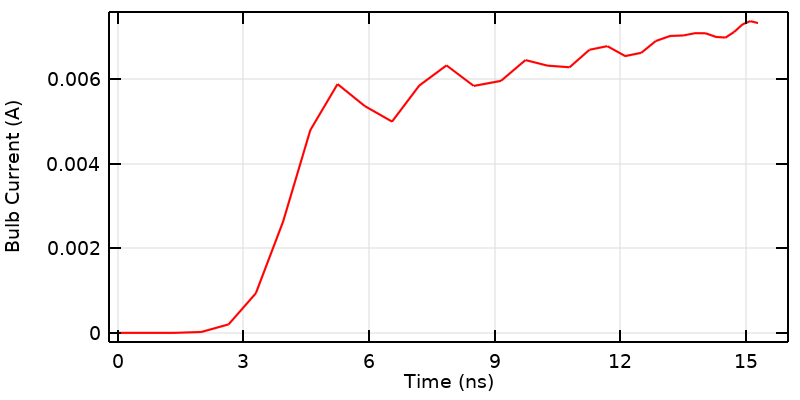
查看开始时间附近的结果,由于我们开关是理想化的,数值方法在模型中人为添加了一些小的色散,这可以看作是真实世界中可能出现的渐变输入信号。
开始时间附近的解
这条曲线的最后一段值得特别注意。在仿真开始时,我们看到信号最初为零,但是在 3.33 ns 之前变为非零。这是一个很小的数值伪影,因为我们正在模拟一种非物理情况:一个瞬间打开的开关。这样的转换在物理上是不可能的:即使是已知最快的物理过程也有阿秒级的上升时间。如果我们关心这部分结果,应该使用具有实际上升时间的瞬态信号替换我们的阶跃变化。我们还必须用精细的时间步长和空间离散化(这可能需要很长时间)来求解我们的数值模型,以使曲线更平滑。
考虑最后一点的另一种方式是,底层的数值方法正在重新添加我们忘记包含的色散。从数值分析专家的专业观点而言,我们可以肯定地说,在现实中,信息的传播速度不会超过光速。
争议的最终结果是什么?
简而言之,最终的结果没有争议。从原始视频中得出的正确结论是,对于所考虑的电路,信号从源传播到灯泡需要 3.33 ns。
更完整的说法是,响应曲线表现出:
- 延迟,这是电磁场通过光源和灯泡之间的空间传播所需时间的结果,在这之后会感应出一些电流。
- RL 电路响应,因为这本质上是一个与电阻器串联的非常大的电感线圈。
- 由于信号在导线中点处急剧弯曲反射而出现的阶梯状平台,其高度由附近平行导线之间的电感和电容耦合决定。
- 由于输入信号的阶跃变化而产生快速波纹,激发了结构的共振。
- 由于灯泡的电阻和辐射,高频部分信号衰减。
在 COMSOL Multiphysics 中构建这样一个模型来验证这种行为既方便、又快速。以下是我们可以查看的其他一些可能的变化:
- 改变电线的半径。这将改变电容耦合的大小,从而改变平台的高度以及纹波的周期。
- 考虑导线的有限导电性。这会降低稳态条件下的电流,但只会在 3.33 ns 之后立即对信号产生非常小的影响。因此,根据阈值,灯泡可能会在 3.33 ns 时被点亮,然后在一段时间后熄灭。
- 改变电线的方向,使两条电线保持靠近,不再朝相反的方向走。在这种情况下,虽然仍然会有一些串扰,但电线的作用更像是传输线。
你还能如何改变这个电路以获得不同的行为?请在下方留下您的想法和评论!
给 COMSOL Multiphysics® 用户的附录
如果您想下载用于生成上述图形的模型并尝试其他情况,可通过以下链接获得教程模型,这是使用RF 模块构建的。此外,我们还有许多其他资源可用于此类建模:
- 要了解有关直流情况下电压和接地的一些基本概念,请参阅博客文章“电压和接地是否存在?”
- 要了解有关该系统的传输线解释的更多信息,请阅读“对波状电磁场建模时的电压和接地”
- 要了解集总端口和集总元件激发的相关内容,请参阅学习中心资源“模拟 TEM 和准 TEM 传输线”
- 要理解为什么这个例子中的信号在 t = 3.33 ns 之前看起来是非零的,了解有限元方法会对您很有帮助,它描述了在空间和时间上的离散问题
- 要了解如何更真实地对开关进行建模,请参阅 COMSOL知识库中的相关内容
- 要查看在更真实的设备上应用的类似建模技术,请查看我们的利用时域反射法测量示例模型
- 要了解有限电导率导致的集肤效应如何发挥作用,以及您需要如何调整计算模型以解决此问题,请参阅博客文章“波电磁学问题中的材料建模”
- 要预测平行线传输线的行为,请参阅COMSOL 案例库中的相关模型教程
- 如果您对无限无噪音宇宙的假设不适应,您可以改为模拟一个放置在全寂室内的系统。从 COMSOL案例库中的条目中了解有关此模型的更多信息
- 如果您想知道在传输线中使用非均匀半径导线会产生什么影响,请阅读博客文章“计算波纹波导的阻抗”
- 如果您想知道为什么我们的模型在导线周围包含如此大的空间区域,请参阅“使用完美匹配层和散射边界条件解决电磁波问题”
- 如果您注意到此模型中的所有场都是中心对称的,并且认为这可以简化模型,那么您是正确的。要了解更多信息,请阅读“利用对称性简化磁场建模”
- 最后,如果您对我最喜欢的电磁学脑筋急转弯问题感兴趣,博客文章“计算直导线的电感”就是其中的一个示例。



评论 (0)