每当你使用 COMSOL Multiphysics 的AC/DC 模块对线圈进行建模时,都需要考虑使用哪种类型的边界条件来截断建模域。在这篇博客中,我们将介绍可以使用的不同边界条件以及如何在它们之间进行选择。
概述:线圈建模的边界条件
上一篇关于线圈建模基础知识的博客文章中,我们提到,无论什么时候对电磁线圈进行建模,都需要从闭合电流环路的角度来考虑。电流环路可以完全在建模域内,也可以通过边界条件闭合,如下图所示。
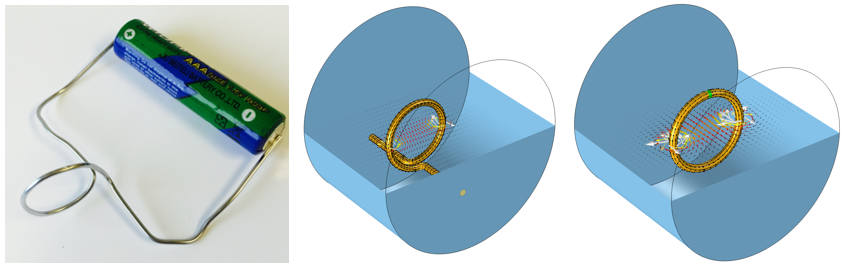
连接到电压源的线圈(左)和两种不同的闭合电流环路的方法(右)。
就像我们之前所了解到的,如果线圈延伸到建模域的边界,那么流过线圈的电流将沿着建模域边界返回。否则,为了使电流环路闭合,线圈就必须在建模域内形成环路。在这里,我们将重点讨论两个问题。首先,我们应该使用哪些边界条件?其次,这些边界应该离线圈多远?
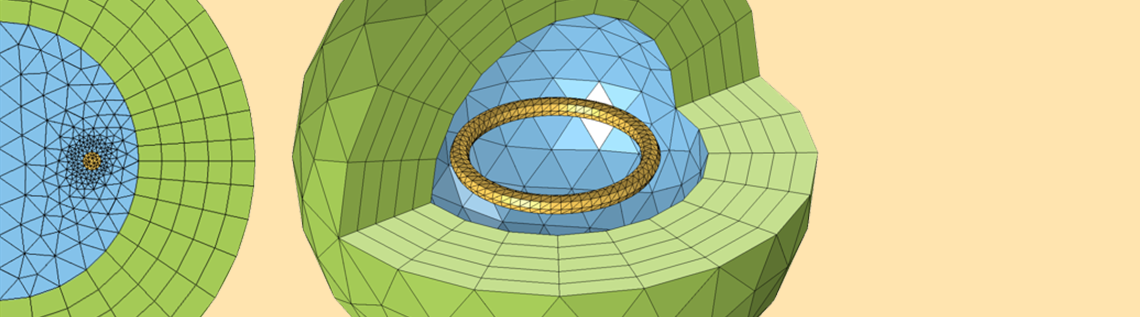
我们先将线圈看作位于一个延伸到无穷大并且不包含其他任何东西的空间中。显然,我们不可能建立一个无限大的域。我们必须将建模域截断为某个有限大小,这样就能在不增加过多计算量的基础上获得合理而准确的结果。首先,让我们考虑在建模域内闭合的轴对称线圈的情况。这种情况可以通过二维轴对称模型进行分析,如下图所示。
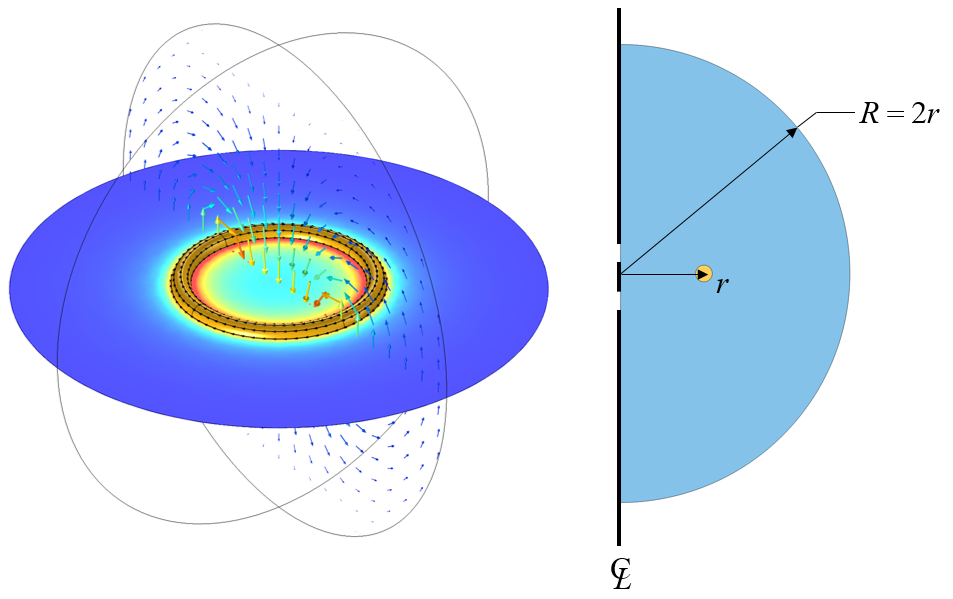
可以通过二维轴对称模型分析球形域内的圆形线圈。对整个研究域的半径根据线圈的半径进行归一化处理。
我们将沿上图所示的建模域的外半径考虑两种不同的边界条件:磁绝缘(MI)边界条件和完美磁导体(PMC)边界条件。磁绝缘条件可以在物理上解释为具有无限导电性的域边界。也就是说,磁绝缘条件意味着线圈被封闭在一个导电率非常高的球壳中。电流可以在磁绝缘边界上流动和感应。从数学上讲,磁绝缘条件将正在求解的场变量固定为边界处为零。它是一个齐次狄利克雷边界条件。
完美磁导体边界条件可以被认为是与磁绝缘条件相反的边界条件。在数学上,它强制执行齐次Neumann 条件,这意味着解场在垂直于边界的方向上的导数为零。即在完美磁导体边界上没有电流可以流动或者感应。
由于这两个边界条件可以被认为是相反的,我们来看看在求解时增大周围空气域的半径会使计算结果发生怎样的变化,并跟踪线圈的电感。我们可以对域半径进行参数化扫描,然后通过合并解来取两个不同边界条件的平均值。计算结果如下图所示,我们可以观察到电感的解随着域半径的增加而收敛,还可以观察到两个解的平均值收敛得更快。
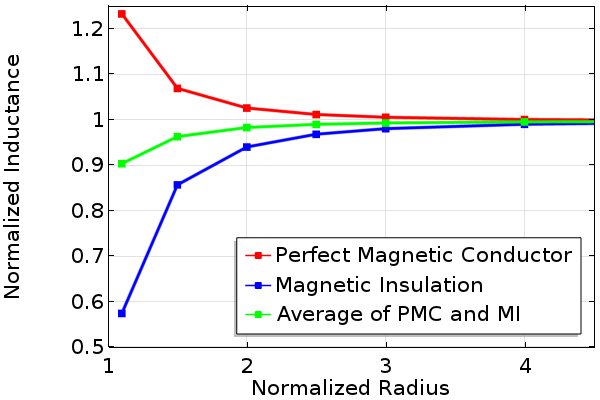
在不同边界条件下,随着建模域半径的增加的线圈归一化电感。
从上面的图中,我们可以得出结论,对于这个轴对称问题,使用哪个边界条件并不重要,只要研究域半径增加的解就可以了。还可以得出,我们可以在相对较小的域半径下运行模型,并同时使用磁绝缘和完美磁导体边界条件获得两种情况下的平均值。即使对于小半径,这个平均值也将很好地预测较大域半径下的解。
用域条件替换边界条件
实际上,我们可以通过使用称为无限元域的域条件截断建模域完全避免边界条件的问题。无限元域要求在建模域的外部周围添加一个附加域作为层。然后,软件在内部执行该域内的坐标拉伸,以使该域无限大,用于所有实际目的。因此,具有无限元域的模型的解将与域半径增加时的解相同。
无限元域的优点是它无需选择边界条件以及域大小。无限元域可以放置在非常靠近线圈的地方,甚至可以与线圈接触。无限元引入的唯一额外工作是模型和网格划分设置。此外,较大的三维模型的求解时间和内存要求可能更大。然而,这些只是为增加便利性而付出的非常小的代价。
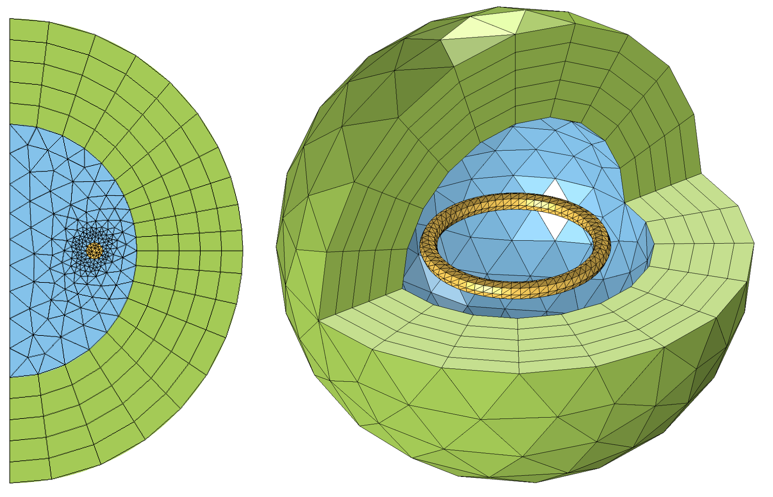
典型二维轴对称域和三维无限单元域的网格。
关于为线圈建模选择边界条件的结束语
在自由空间中对电磁线圈进行建模时,我们研究了三种不同的截断域的方法:磁绝缘边界条件、完美磁导体边界条件和无限元域。使用磁绝缘和完美磁导体边界条件时,必须研究域半径增加的模型收敛性,以及随着域半径的增加,解将全部收敛到相同的值。取两种情况的平均值可以预测在较大的域半径下会发生什么。你也可以尝试使用无限元域来得到相同的答案。
如果线圈延伸到建模域的边界,就需要通过磁绝缘边界条件提供电流返回路径。如果存在表示金属外壳的域边界,并且是在频域中建模,那么还要关注阻抗边界条件,这对于模拟有损材料(如金属)很有用。
如果你有一个对称性的模型,还可以使用磁绝缘和完美磁导体边界条件来强制实施不同类型的对称性, 具体可以参阅利用对称性简化磁场建模这篇博客文章。
更多资源
如果你刚开始学习使用 COMSOL Multiphysics 的 AC/DC 模块进行线圈建模,还可以看看以下案例模型:
- 电感器3D建模
- 功率电感器的电感
- 亥姆霍兹线圈的磁场
- 不对称导体板上的多匝线圈
- 绕在铁磁体周围的多匝线圈
- 单匝线圈之间的互感和感应电流
- 线圈组中的互感和感应电流
- 多匝线圈中的互感和感应电流
- 螺旋电感线圈建模
- 集成电路方形螺旋电感器
你还希望使用 COMSOL Multiphysics 和 AC/DC 模块进行哪种线圈建模?欢迎联系我们。



评论 (0)