
欢迎回到我们关于高频电磁中多尺度建模的讨论。当一个模拟中存在相差极大的不同的尺度时,多尺度建模是一次模拟挑战。例如,天线尺寸与天线距其接收目标之间的距离相比,就属于多尺度。今天,在本系列博客的第4部分中,我们将研究如何通过射线光学模块将全波天线模拟与几何光学模拟耦合起来建立多尺度模型。
使用射线光学模块进行多尺度建模
在本系列博客的第 2 部分中,我们使用了电磁波,频域接口(称为全波仿真)和远场域节点来确定远场中的电场。然后,将全波仿真与电磁波,波束包络接口(或波束包络仿真)耦合,以便精确计算任何区域中的场,无论该区域与源相距多远。
在上一篇博文中介绍的远场域和波束包络解是有效的,但它们有一个限制。在每种情况下,我们均假设在天线周围所有方向上存在一个均匀的域。在许多情况下,有此条件就足够了。但在其他模拟中,天线周围可能没有均匀的域,因此我们需要解决诸如大气折射或附近建筑物反射的问题。这种模拟需要不同的方法。
Las Vegas(拉斯维加斯)的几家酒店的模型。一个定向天线向 ARIA®Resort&Casino 辐射射线。
射线光学模块(COMSOL Multiphysics® 软件的附加产品)中的几何光学接口将EM(电磁)波视为射线。该接口可以计算空间变化的折射率,复杂几何形状的反射和折射以及长距离传播。但是,这些功能需要权衡。由于将波视为射线,因此该方法忽略了衍射。换句话说,我们假设光的波长比我们环境中的任何几何特征小得多。您可以在以前的博客文章中阅读有关射线光学更详尽的描述。
天线耦合建模:为射线光学做准备
您可能还记得,在本系列博客的第 3 部分中,我们介绍了一种耦合辐射和接收天线的方法。当将射线光学系统纳入多尺度建模时,我们需要使用一种与之类似但更通用的方法。在介绍如何在 COMSOL Multiphysics 中设置几何光学仿真之前,让我们先回顾一下这种替代方法。
绘制辐射场
作为快速复习,我们使用以下公式计算接收天线位置处的场:
以前,我们在单个点上使用了积分算子,以沿两个天线的直线距离直接计算该值。现在,我们希望保留角度依赖性,因此我们需要为接收天线域中的每个点重新计算该方程。由于添加许多点和积分算子是不切实际的,因此我们需要建立一种更通用的技术。
为此,我们用广义拉伸算子替换了积分算子。和以前一样,我们为r的大小创建一个变量。然后,使用广义拉伸算子评估几何中共享相同角坐标的点处的散射幅度,(\theta,\phi),这才是我们真正感兴趣的地方。
为了演示这个概念,我们使用了一个比上一篇文章稍微复杂的图形。需要注意的是下标 1,2,和\vec{r}_j=\left(x_j,y_j,z_j\right)中的r分别表示分量 1 中的向量,分量 2 中的向量,以及天线之间的偏移。
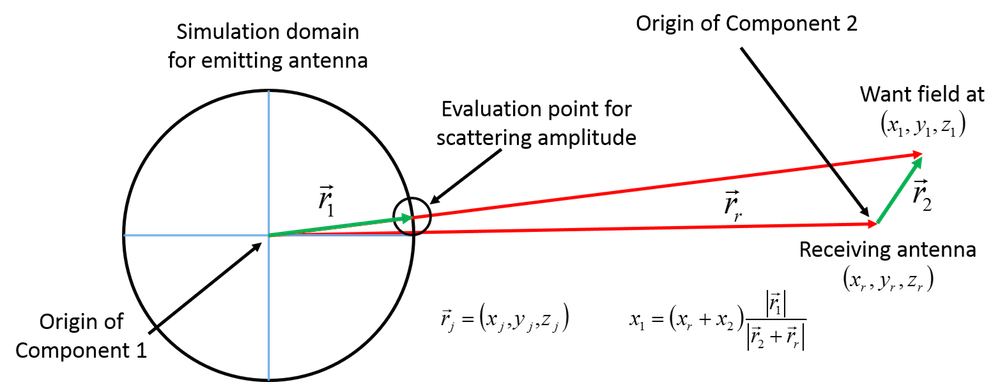
图中显示了应该在哪里计算散射幅度以及如何确定该点的坐标。
正如我们之前概述的那样,确定在哪里计算散射幅度是首要问题。要知道点\vec{r}_r + \vec{r_2}处的场,这需要计算\vec{r}_1处的散射幅度。该计算的复杂之处在于,接收天线周围域中的每个点(每个向量\vec{r}_2)将有自己的评估位置\vec{r}_1。我们可以通过重新调整直角坐标的坐标来对此进行评估,但不是对单个点进行缩放,而是在常规算子内部定义它,以便可以从任何位置调用它。从上图中,我们知道这个点是x_1 = \left(x+x_r\right) \frac{|\vec{r}_1|}{|\vec{r}_2+\vec{r_r}|},y 和 z 也是用对应的方程计算。该算子是在组件 1 中定义的,因此将在该组件中定义源。它将从组件 2 中调用,因此下列表达式中的x,y,z表示上图中的x2,y2,z2。

广义拉伸算子用于散射幅度计算。请注意,这是在组件 1 中定义的。
在虚拟变量中存储辐射场
作为统计步骤,我们将计算出的场存储在“虚拟”变量中。虚拟变量是指我们添加一个额外的因变量,该因变量采用在其他地方确定的计算值。我们这样做有两个原因。
第一个原因是,COMSOL Multiphysics 中的大多数变量都是根据需要从因变量中计算得出的。例如,在 RF 仿真中,因变量是电场的三个笛卡尔分量:Ex,Ey 和 Ez。这些是在计算解时确定的。当需要时,在后处理中根据电场计算出其他所有值(电流,磁场等)。在大多数情况下,这是一个快速且无缝衔接的过程。在我们的案例中,每个场评估点都需要对散射振幅进行广义拉伸,并且每个散射振幅点都需要一个在远场域节点中定义的表面积分。这可能需要一段时间,我们希望确保仅执行一次该计算。
我们这样做的第二个原因与单元阶次有关。该散射场公式需要一个背景电场。COMSOL Multiphysics使用法拉第定律的微分形式(也称为麦克斯韦-法拉第方程)来计算磁场。这需要获取电场的空间导数。对平面波或高斯光束等解析函数求空间导数没有问题,但是将其应用于已求解变量时会导致离散问题。这是一个相当高级的主题,您可以在基于方程建模的 COMSOL 网络研讨会中找到更多信息。
通过使用一个三次虚拟变量来存储电场,我们可以获取电场的空间导数,并且获得一个解析度很高的磁场以用于散射场公式。如果不增加虚拟变量的阶数,将无法充分解析所使用的磁场。下面,您可以看到将广义拉伸算子与虚拟变量设置放在一起的样子。变量r与本系列博客第3部分中使用的变量相同,并被定义在组件 2 中。
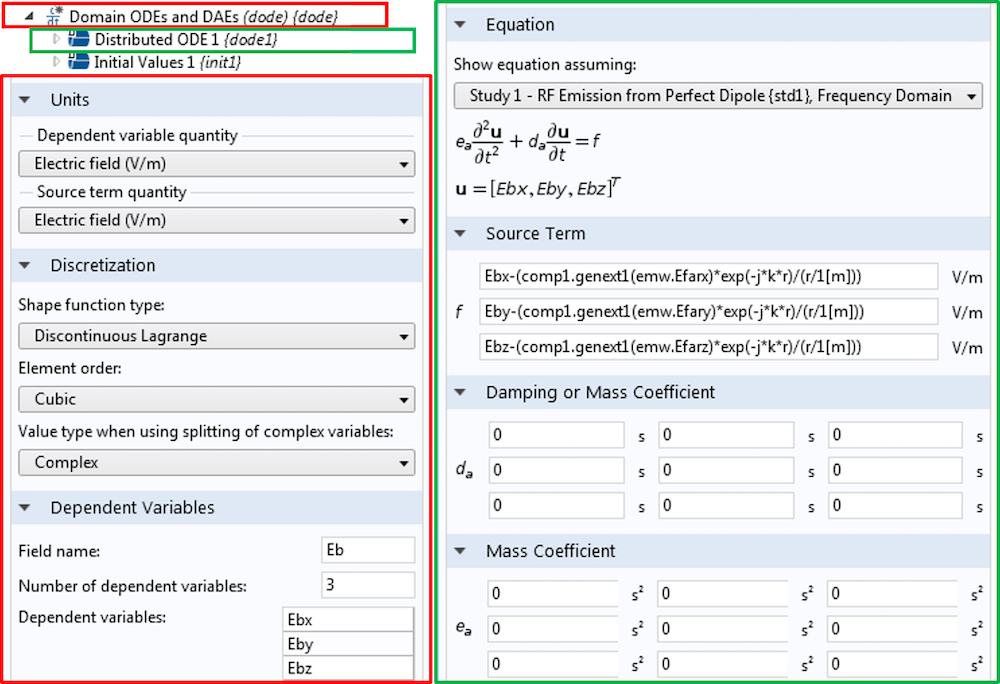
实现的虚拟变量。请注意,虚拟变量组件称为 Ebx,Eby 和 Ebz。
仅剩的步骤是在第 1 部分和第 3 部分博客中讨论的半波长偶极子的背景场模拟中使用虚拟变量 Ebx,Eby 和 Ebz 。
对于这个特定问题,该方法实际上并不是很好。在某些情况下,它很有用,但是在大多数情况下,第3部分博客中使用的方法是首选。来自两个模拟的接收功率非常接近,但是此方法需要花费更长的时间进行计算,并且文件大小急剧增加。在本文的演示示例中,此方法花费的时间比以前的模拟方法长几倍。虽然你可能会认为这并不是一个非常有用的步骤,,但是,如下一节所述,当我们将射线光学技术集成到多尺度建模中时,这将非常有用。
在 COMSOL®软件中设置几何光学仿真
几何光学仿真隐性假设每条光线已经在远场中。在系列博客的较早版本中,我们看到远场域功能可以正确计算远场中任意点处的电场。在这里,我们将这些信息用作几何光学仿真中射线的输入。使用的仿真几何形状,对称性和电偶极点源与第 2 部分博客中的相同。
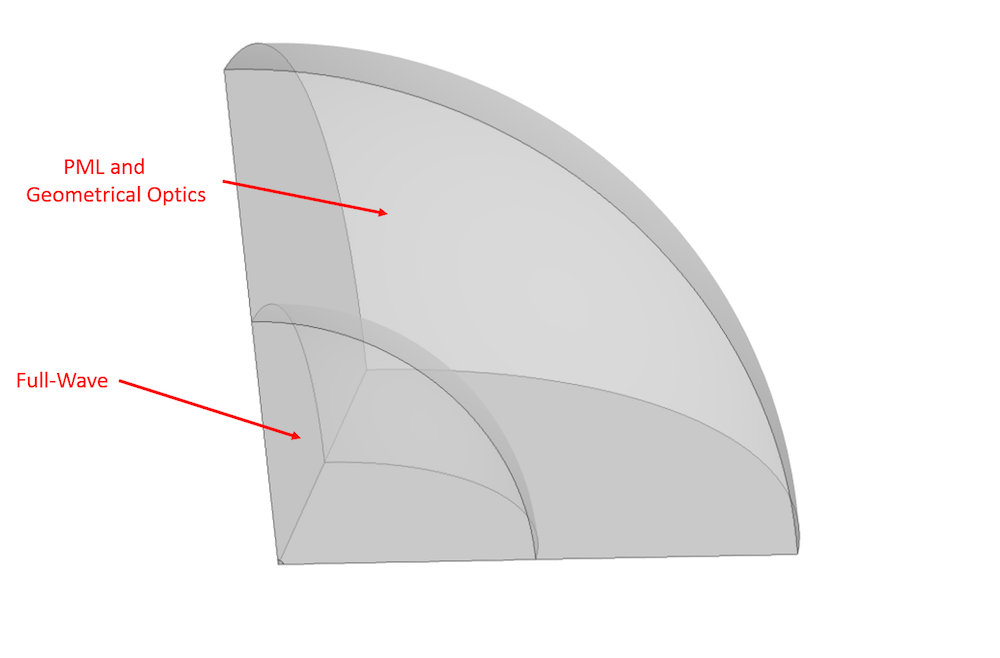
模拟域的分配。在整个域中执行“全波”仿真,外部区域设置为完全匹配层(PML)。仅在此外部区域中执行几何光学仿真。请注意,此图像未按比例绘制。
分配域之后,选择几何光学接口,将强度计算更改为计算强度,然后选中计算相位复选框。需要这些步骤才能正确计算沿射线轨迹的电场的幅度和相位。
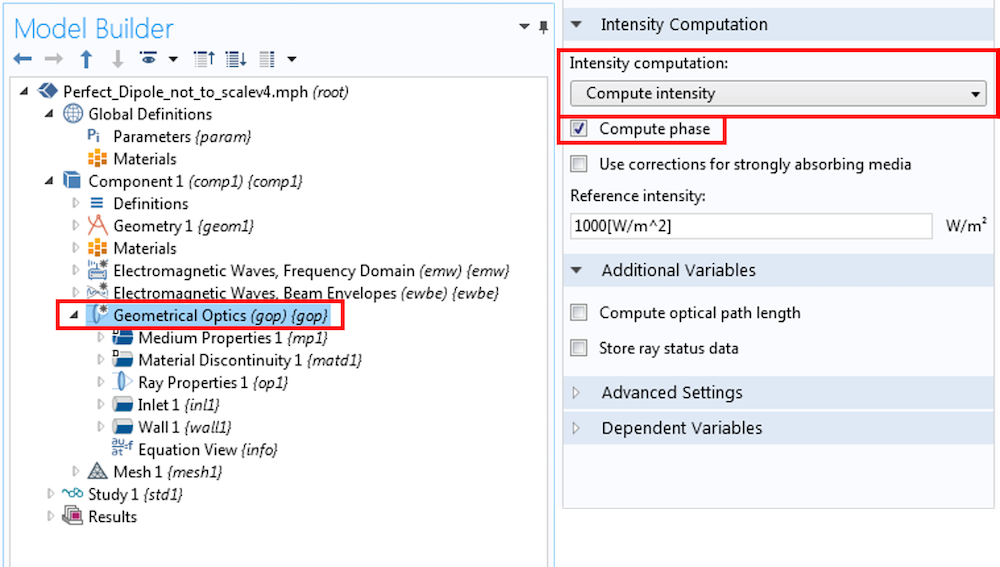
几何光学接口的设置。强度计算被设定为计算强度,并选中计算相位复选框。
我们还将入口边界条件应用于全波模拟域和几何光学域之间的边界。入口设置可以在下图中看到,我们一次来浏览一个。首先,配置射线方向矢量部分,这将发出垂直于我们为入口选择的曲面的射线,换句话说,沿径向向外。变量Etheta可以根据
计算得到,Ephi 的计算与之类似。
该方程来自之前的博客文章,内容涉及使用远场域节点来计算任意位置的场。这些变量用于指定光线的初始相位和偏振。变量GOP\_I0为射线指定正确的空间强度分布(因为天线通常不会均匀发射),并根据GOP\_I0 = (|Etheta|^2 + |Ephi|^2)/Z/2计算,其中Z是介质的阻抗。
初始曲率半径有两个因子。参数dipole\_sim\_r是发出光线的球面边界的半径,它将正确初始化光线波前的曲率。
最后,我们使用球形单位矢量的笛卡尔分量\hat{\theta}指定初始主曲率方向。这确保了将正确的偏振赋予光线。这里的波阵面形状必须设置为椭圆(即使从理论上说该表面是球体),因为我们需要能够指定极化的首选方向。如果选择Spherical,则每个方向都会简并,因此无法指定方向

几何光学接口中入口边界条件的设置。请注意,您可以单击图像将其展开。
除了设置正确的频率以外,唯一的额外设置是在外部边界上设置“冻结”的“壁”条件以使射线停止。让我们看一下结果与理论。如前所述,我们将点偶极子的完整解表示为两个贡献之和,并将其标记为近场(NF)和远场(FF)。
\overrightarrow{E} & = \overrightarrow{E}_{FF} + \overrightarrow{E}_{NF} \\
\overrightarrow{E}_{NF} & = \frac{1}{4\pi\epsilon_0}[3\hat{r}(\hat{r}\cdot\vec{p})-\vec{p}](\frac{1}{r^3}+\frac{jk}{r^2})e^{-jkr}\\
\overrightarrow{E}_{FF} & = \frac{1}{4\pi\epsilon_0}k^2(\hat{r}\times\vec{p})\times\hat{r}\frac{e^{-jkr}}{r}\\
\end{align}
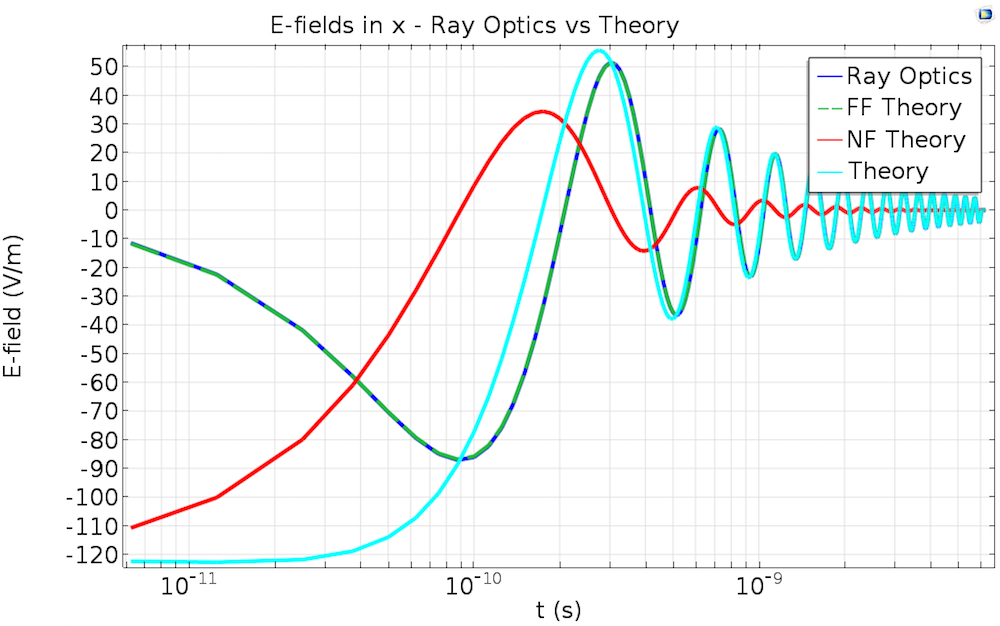
将几何光学仿真中的电场与理论进行比较。几何光学始终处于远场,因此,随着距光源的距离增加,我们会看到极好的一致性。作为参考,前一篇文章的远场域结果将与射线光学和 FF 理论线完全重叠。
如前所述,几何光学接口必定计算远场信息,因此我们并不希望像在第 2 部分博客的波束包络解中那样能够正确捕获近场信息。我们将来自远场域节点的计算数据用于光线追踪模拟。因此,在光源附近的结果存在分歧并不令人惊讶,但是随着与源的距离增加,我们可以清楚地看到该结果与理论相符。
多尺度建模技术总结
如果仅看上面的内容,我们必须问自己:“我们在这里实际获得了什么?”
这是一个公平的问题,因为上面显示的图可以使用到目前为止该系列中介绍的任何方法直接得到。为了清楚起见,让我们来复习一下。
| 多尺度技术 | 有效区域 | 使用的模块 | 说明 |
|---|---|---|---|
| 远场域节点 | 远场 | RF 或波动光学 | 要求天线被均匀材料完全包围 |
| 光束包络 | 任何场 | 波动光学 | 需要指定相函数或波矢量 |
| 几何光学 | 远场 | 射线光学 | 可以计算空间变化指数以及复杂几何形状的反射和折射,忽略衍射 |
本系列博客中介绍的多尺度建模技术总结
注意,任何这些技术都需要对辐射源进行全波仿真。尽管有一部分辐射源可以使用波动光学模块建模,但这通常需要RF模块。在远场域节点RF模块和波动光学模块都可用。
最初,我们通过讨论从一个天线到另一个天线的信号传输来激发这一讨论的,并在上一篇文章中使用远场域节点求解该模拟问题。在本系列的下一篇博客文章中,我们将使用此处介绍的几何光学接口重做该模拟。
单击上面的按钮,访问本博客文章中讨论的模型以及本系列博客中突出显示的任何模型示例。
ARIA 是 CityCenter Land,LLC 的注册商标。



评论 (2)
云鹏 许
2024-05-11请问什么时候出介绍几何光学接口重做该模型的文章呢?
Min Yuan
2024-05-14 COMSOL 员工您好,可以持续关注官网相关内容,如果有更新,将在官网发布。