
之前我们学习了如何在 COMSOL Multiphysics®软件中计算 Fraunhofer 衍射模型中矩形孔径的傅里叶变换。在该案例中,孔径是作为一个解析函数给出的。如果用于傅里叶变换的源数据是计算得到的解,那么变换过程会有所不同。在本篇博客文章中,我们将学习如何由菲涅尔透镜(Fresnel lens)电磁模拟的计算解实现傅里叶变换。
用傅里叶光学进行傅里叶变换
在仿真中实现傅里叶变换可用于傅里叶光学、信号处理(用于频率模式提取)以及通过图像处理进行降噪和滤波等。在傅里叶光学中,菲涅尔近似是计算衍射孔径附近场的近似方法之一。假设衍射孔位于z=0的(x,y)平面,在(u,v)平面,距离衍射孔径z=f处的衍射电场可由下式计算
{i\lambda f}
e^{i2\pi f /\lambda} e^{-i\pi(u^2+v^2)/(\lambda f)} \iint_{\infty}^
{\infty}
E(x,y,0)e^{-i \pi(x^2+y^2)/(\lambda f)}e^
{i2 \pi (xu+yv)/(\lambda f)}
dxdy,
其中,\lambda是波长,E(x,y,0), \ E(u,v,f)分别代表(x,y)平面和(u,v)平面的电场。(有关更多详细信息,请参阅参考文献1)
在该近似公式中,通过对入射场乘以二次相位函数{\rm exp}{-i\pi (x^2+y^2)/(\lambda f)}进行傅里叶变换来计算衍射场。
相位函数的符号约定必须遵循电场的时间相关性的符号约定。在 COMSOL Multiphysics 中,电磁场的时间相关性具有以下形式:{\rm exp}
(+i\omega t)。因此,二次相位函数的符号为负。
菲涅尔透镜
现在,我们来看一个菲涅尔透镜的例子。除了其弯曲表面外,菲涅尔透镜是一种规则的平凸透镜,它沿透镜高度在每m\lambda/(n-1)倍数处都向平边折叠,其中m是整数,n是透镜材料的折射率。这就是 m 阶菲涅尔透镜。
表面沿光传播方向移动此特定高度只会改变光的2m\pi相位(粗略地说,在傍轴近似下)。因此,折叠透镜基本上会在远场再现相同的波前,并表现得像原始的未折叠透镜一样。其主要的区别在于衍射效应:普通透镜基本上不显示任何衍射(如果没有通过硬光阑产生的渐晕现象),而菲涅尔透镜由于表面不连续和内部反射,在主光斑周围总是会显示出小的衍射图样。
当菲涅尔透镜被数字化设计时,透镜表面由离散层组成,使其外观呈阶梯状,这被称为多级菲涅尔透镜。由于阶梯具有平坦的部分,因此除了高阶衍射之外,多级菲涅尔透镜的典型衍射图案通常还包括零阶背景。

波士顿的一座灯塔中的菲涅尔透镜。图像由 Manfred Schmidt 提供-自己的作品。通过Wikimedia Commons在CC BY-SA 4.0下获得许可。
为什么我们要以菲涅尔透镜为例?其原因与在灯塔运行中使用菲涅尔透镜的原因类似。菲涅尔透镜被折叠成m\lambda/(n-1)的高度,它非常薄,与传统折射透镜的大、重、厚相比,菲涅尔透镜的重量和体积更小,这有利于灯塔的光学系统。同样,我们也可以根据使用目的来控制菲涅尔透镜元件的数量,从而更轻松地在 COMSOL Multiphysics 和附加的波动光学模块中进行模拟。
在 COMSOL Multiphysics®中模拟聚焦菲涅尔透镜
下图描述了我们试图模拟的光学设置,以演示如何对通过波动光学,频域接口求解的解实现傅里叶变换。
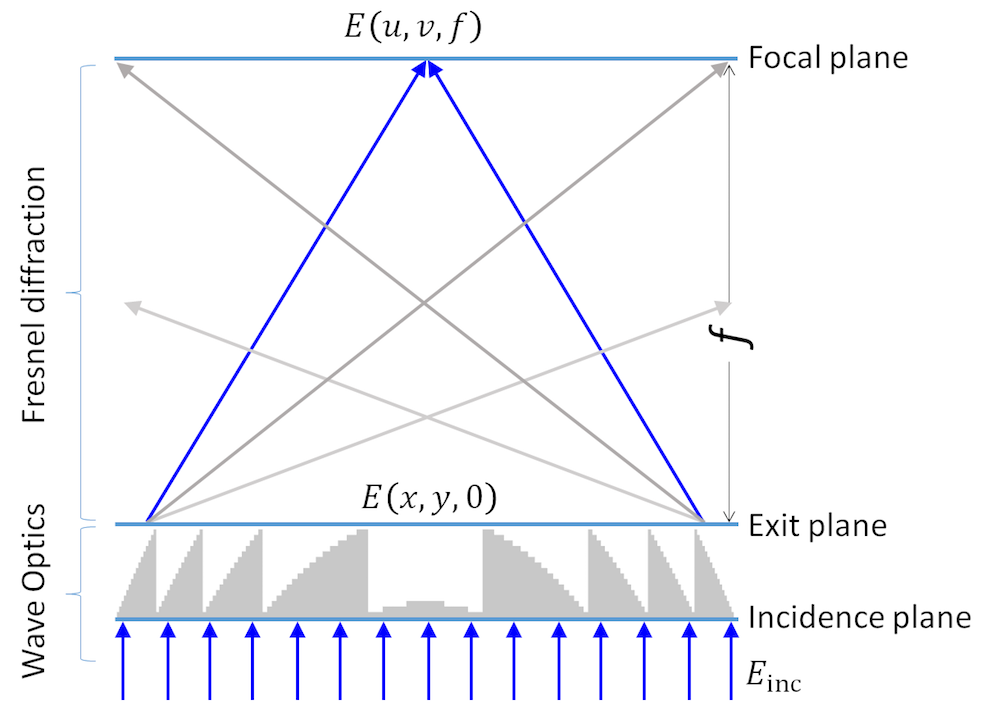
聚焦的 16 级菲涅尔透镜模型。
这是一个一阶菲涅尔透镜,其表面被数字化为 16 级。一束平面波E_{\rm inc}打到入射平面上,在出口平面z=0处,该场被菲涅尔透镜衍射为E(x,y,0)。该过程可以通过波动光学,频域接口进行建模和仿真。然后,我们通过在菲涅尔近似下应用傅里叶变换计算焦平面z=f处的场E(u,v,f)。
下图是我们计算的结果,电场分量分布在域中(顶部)和与出口平面相对应的边界处(底部)。请注意,几何图形在垂直轴上没有按比例绘制。我们可以从中心和锯齿间的每个气隙清楚地看到正弯曲的波前。注意,来自透镜表面的反射会造成域场结果中的一些小干扰和边界场结果中的波纹。这是因为这里没有建里抗反射涂层的模型。

菲涅尔透镜和周围空气域中计算出的电场分量(垂直轴未按比例绘制)。
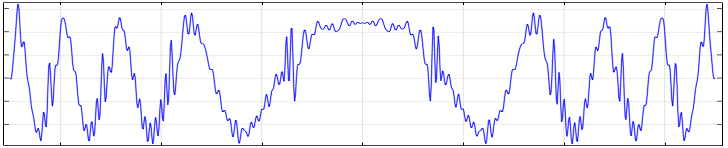
在出口平面上计算出的电场分量。
通过计算解实现傅里叶变换
继续进行傅里叶变换。在前面的解析函数示例中,我们准备了两个数据集:一个用于源空间,另一个用于傅里叶空间。在数据集的设置窗口中定义的参数名称是在源平面的空间坐标(x,y)和在图像平面中的空间坐标(u,v)。
在今天的这个示例中,我们已经使用计算解在计算的数据集 Study 1/Solution 1(sol1){dset1}中 创建了源空间。我们需要做的就是创建一个包含傅里叶空间参数的一维数据集 Grid1D{grid1},即焦平面中的空间坐标u。然后,将其与源数据集相关联,如下图所示。我们在出口平面上定义一个积分算子intop1。
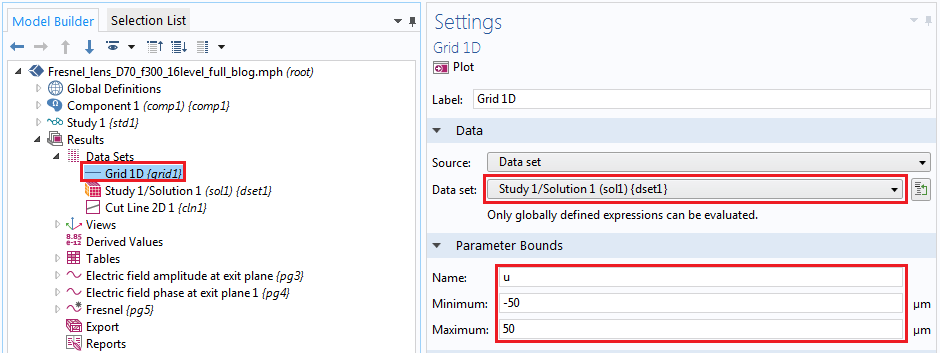
变换数据集的设置。
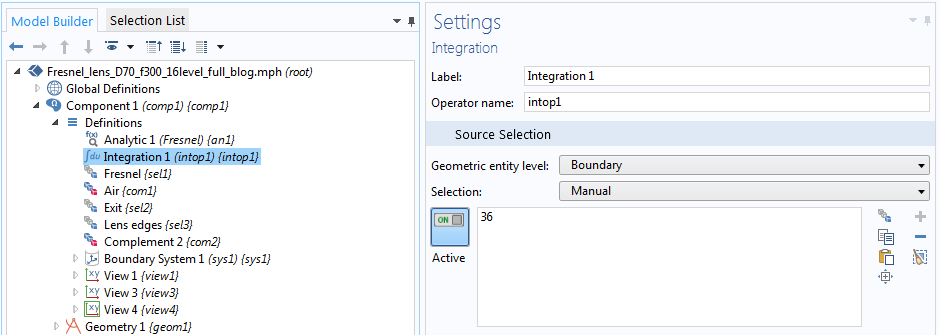
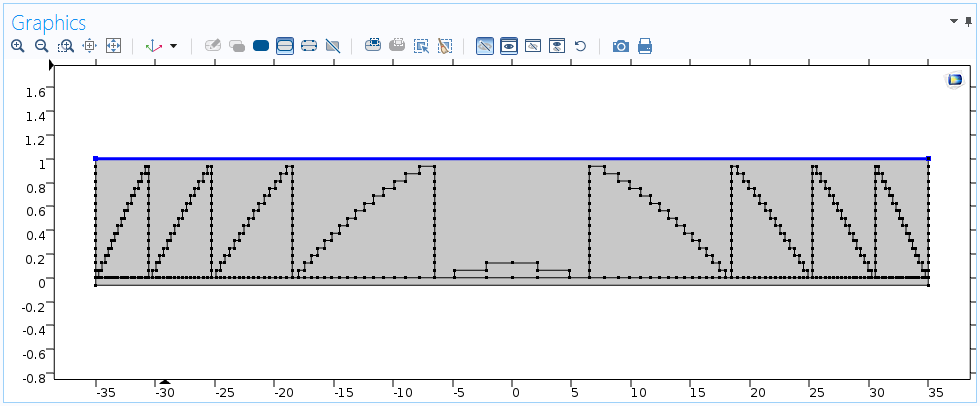
在出口平面上定义的运算符intop1(垂直轴未按比例绘制)。
最后,我们在一维绘图中定义傅里叶变换,如下图所示。这里重要的是要指定我们之前为变换创建的数据集,并让 COMSOL Multiphysics 知道是使用dest算子的目标变量。
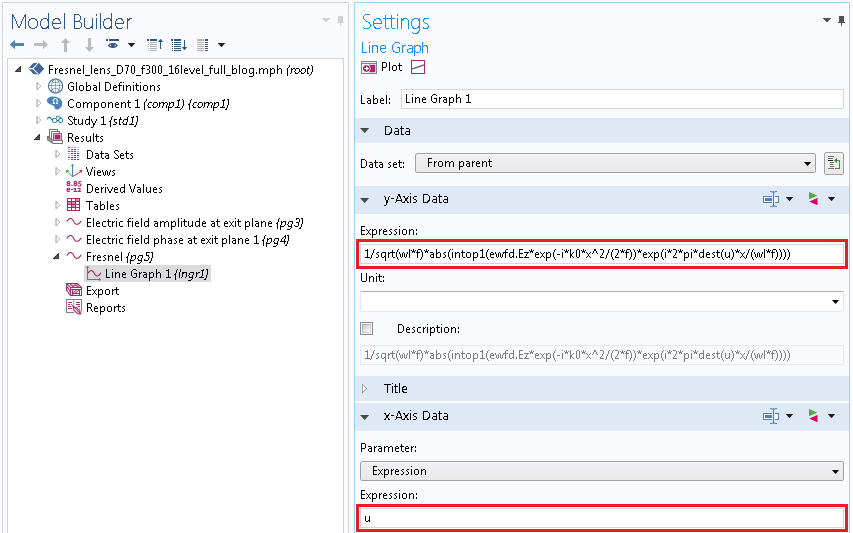
COMSOL 软件中一维绘图中傅里叶变换的设置。
下图显示了最终的结果。这是聚焦光束通过多级菲涅尔透镜焦平面的典型图形(请参阅参考文献2),中心处存在一阶衍射的主光斑以及一个由零阶(非衍射)和高阶衍射引起的较弱的背景。
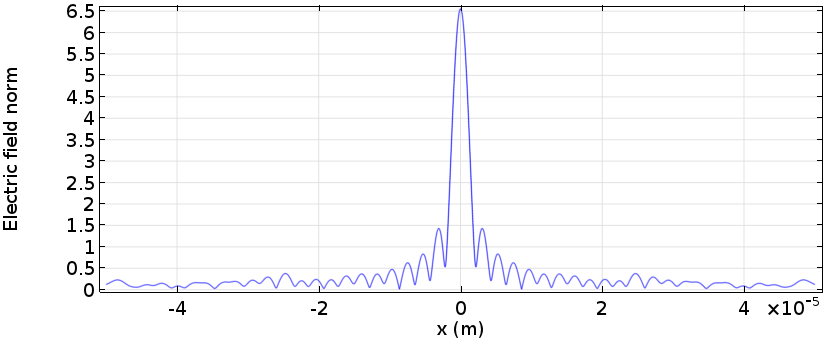
聚焦光束通过 16 级菲涅尔透镜的电场模图。
结语
在本篇博客文章中,我们学习了如何对计算解实现傅里叶变换。该功能对于 COMSOL Multiphysics 中的远距离传播计算非常有用,并将电磁仿真扩展到了傅里叶光学。
后续操作
单击下面的按钮,下载菲涅尔透镜示例的模型文件。
了解有关波动光学模拟的更多信息
参考文献
- J.W. Goodman,Introduction to Fourier Optics, The McGraw-Hill Company, Inc.
- D. C. O’Shea,Diffractive Optics, SPIE Press.



评论 (0)