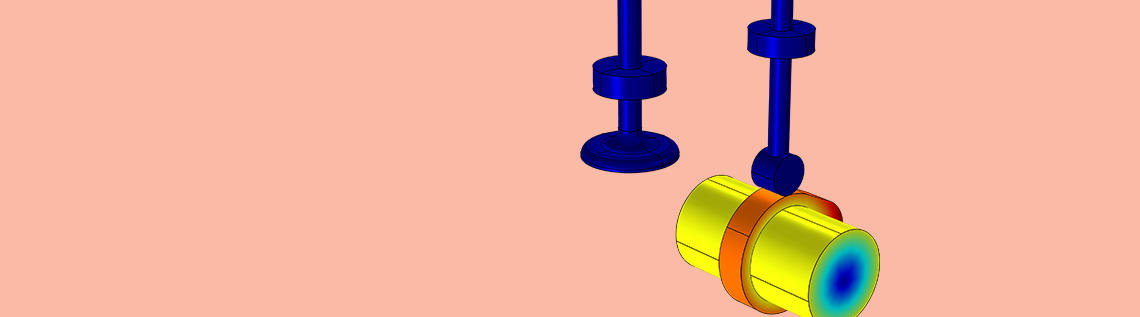
使用多体系统时,我们可能需要为一个将运动从一个组件转移到另一个组件的机构进行建模。这种构件称为凸轮-从动件,它在许多应用中发挥着重要作用,包括内燃机、印刷控制机构、纺织机和阀门。我们可以使用 COMSOL®软件的凸轮–从动件特征轻松地模拟此类机构。今天,我们来详细了解一下这个功能。
对不同类型的凸轮-从动机构进行分类
凸轮-从动机构的分类是根据其配置的输入和输出运动进行的。下面,我们来介绍不同类型的凸轮-从动机构。
旋转凸轮,平移从动件
当凸轮旋转时,从动件沿导轨移动,这种运动可分为旋转凸轮和平移从动件。根据从动件的运动进一步分类。如果运动是沿着穿过凸轮旋转中心的轴,则称为径向直线从动件,而如果运动是沿轴偏移,则称为径向偏移从动件。
动画显示了径向直线从动件的位移和速度图。
动画显示了径向偏移从动件的位移和速度图。
旋转凸轮,摆动从动件
当凸轮的旋转运动转换为振荡运动时,这种配置被称为旋转凸轮和摆动从动件。
动画显示了一个摆动凸轮和从动件示例。
平移凸轮、平移从动件
在这种情况下,凸轮和从动件都表现出平移运动。这意味着从动件的运动是由凸轮的轮廓高度引起的。
动画显示了一个楔形凸轮的位移图。
静止凸轮,移动从动件
在某些情况下,凸轮是静止的,从动件跟踪凸轮的轮廓。这种类型的布置被归类为静止凸轮和移动从动件。
动画显示了静止凸轮和移动从动件的位移图。
点从动件
点从动件是一种从动件上的销在槽中滑动的机构。插槽可以是任意形状。
动画显示了在弯曲槽中移动的销的位移图。
组合运动
有很多方法可以将一种运动转换为另一种运动。凸轮从动机构的多样性仅限于我们想象力的限制。例如,我们可以使用上述配置的组合来生成组合效果。一些常见的例子是桶形凸轮和端部凸轮,它们用于将旋转运动转换为平移和振荡运动。
动画显示了一个桶形凸轮的平移和振荡运动组合。
使用凸轮-从动件连接类型
从 COMSOL Multiphysics® 软件 5.3a 版本起,多体动力学模块提供了凸轮–从动件连接类型,用于模拟点跟随曲线的应用。换句话说,就是接触是唯一的并且发生在一个点上。
通常,主动件称为凸轮,被动件称为从动件,但在 COMSOL® 软件中,这个内置的功能可以允许我们将两个组件建模为主动或被动组件。
在默认设置下,凸轮和从动件将始终保持接触,这意味着不允许振动。如果要模拟间歇接触,我们可以使用凸轮从动件关节类型下的激活条件功能。此外,凸轮和从动件都可以建模为刚性或柔性组件。
为了确保从动件上的点始终跟随指定的凸轮表面,定义了与凸轮边界的偏移,以使间隙距离始终为零。这些约束的实现遵循以下过程:
- 基于选定的凸轮表面,使用搜索算法找到凸轮表面上相对于指定从动点最近的点
- 定义内部间隙变量,以便将从动件上的点与凸轮上的最近点之间的绝对矢量差设置为预定义的偏移量
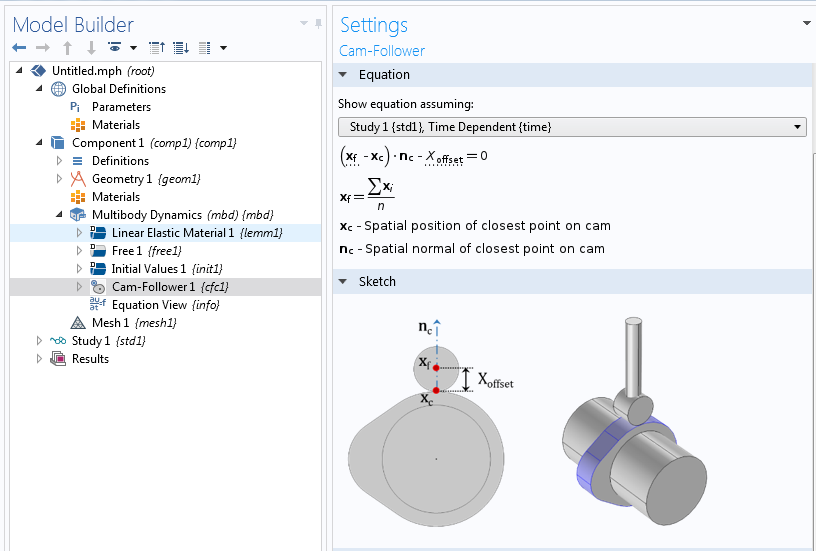
COMSOL Multiphysics 附加的“结构力学模块”和“多体动力学模块”中的凸轮从动件特征的方程和草图。
如果你对公式的细节不感兴趣,可以跳到下一节。
为了理解公式,让我们看一个凸轮和滚子配置的例子,其中凸轮和滚子都被建模为刚性组件。对于刚性体,可以通过固定(局部)坐标系 (X, Y) 的原点定位物体上的点。由于点固定在物体上,所以向量的元素在物体固定坐标系中是恒定的,而在全局坐标系中,它们随着旋转而变化。从局部到全局方向的转换用旋转矩阵表示。
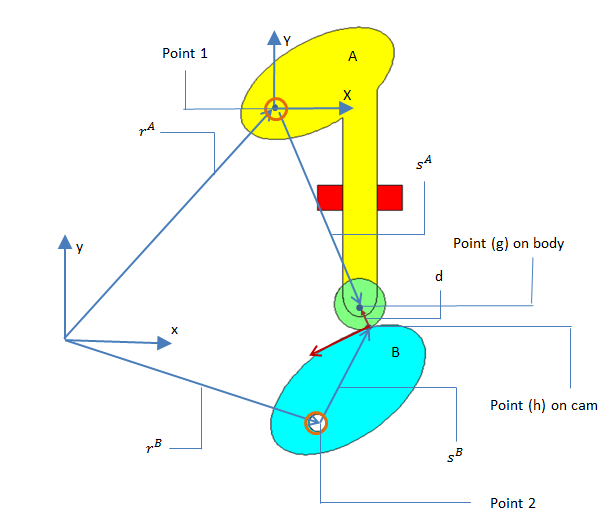
凸轮和滚子配置示意图。
现在,点 (P) 在物体 (i)上的绝对位置可以表示如下:
其中,点 (c) 的位置是使用刚体的旋转中心计算的,它也用作固定坐标系的原点。
- x= 全局x轴
- y= 全局y轴
- rA= 物体 A 旋转中心的绝对位置
- sA= 物体 A 上点 (g) 相对于旋转中心的全局位置向量
- rB= 物体 B 旋转中心的绝对位置
- sB= 物体 B 上点 (h) 相对于旋转中心的全局位置向量
- RA= 点 (g) 相对于空间坐标系的绝对位置
- RB= 点 (h) 相对于空间坐标系的绝对位置
所以,
由于公共接触点相对于物体 (A) 和 (B) 不是固定的,因此需要在两个物体之间定义约束以保持连续接触。
在 COMSOL Multiphysics 中,约束定义在向量 d 上,使其在凸轮表面上最近点的法线方向上的大小等于偏移值。
基于径向凸轮的阀门开度机构建模
在我们的例子中,考虑一个用弹簧加载的阀门开启机构,它有一个摇臂和一个径向凸轮。在这种机构中,凸轮旋转是规定的,并且弹簧连接到阀门上以限制其运动。
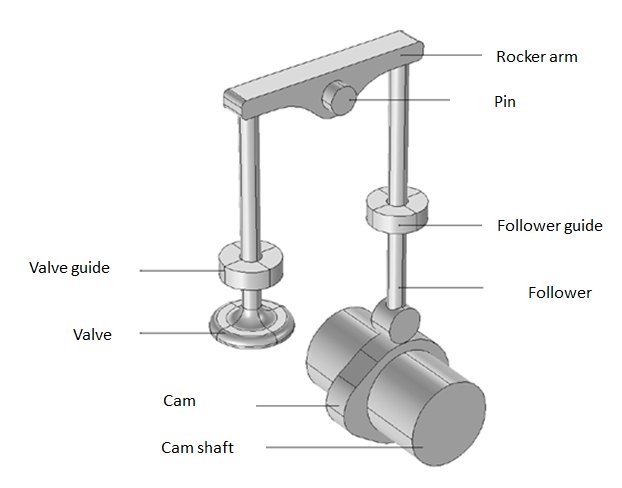
带有摇臂和径向凸轮的阀门开度机构的几何形状。
这种分析的目的有两个:
- 计算给定凸轮轴 转速下从动件的位移、速度和加速度
- 计算不同的阀门弹簧刚度下,在给定转速下旋转凸轮凸轮从动件所需的的连接力和扭矩
在阀门上安装弹簧的主要目标之一是迫使从动件跟随凸轮轮廓并避免凸轮和从动件之间的间歇性接触。因此,阀门弹簧刚度的最佳值应该始终加强凸轮和从动件之间的接触,同时要求转到凸轮轴的扭矩最小。
在 COMSOL Multiphysics® 中评估仿真结果
显示径向凸轮位移图的动画。
当从动件与凸轮轮廓的开口侧面区域接触时,从动件速度首先增加。之后,它会减小,并在机头区域减小变为零。类似地,当从动件与凸轮轮廓的愈合区域接触时,速度沿相反方向增加并变为零。在 COMSOL Multiphysics 中,关节的速度和加速度符号约定是根据指定的关节轴确定的。如果目标附件沿关节轴的正方向移动,则为正。对于这种情况,关节轴是沿z轴定义的,因此当从动件向上移动时速度为正,反之亦然。
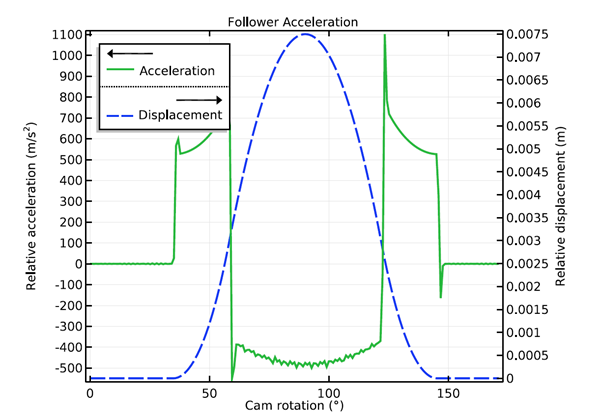
从动速度(左)和从动加速度(右)随凸轮旋转的变化。
我们可以看到,在凸轮旋转 60° 到 120° 的范围内,加速度值为负。这是从动件倾向于离开与凸轮轮廓接触的区域,取决于给定凸轮轴 转速的阀门弹簧刚度值。通过绘制连接力与凸轮旋转的关系图,我们可以检查哪个弹簧可确保连续接触。如果凸轮和从动件不再接触,则接触力符号约定为正,而负值表示仍保持接触。
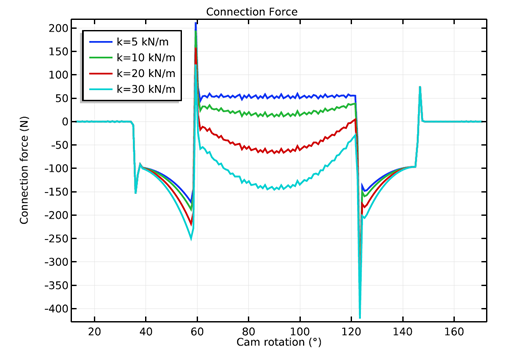
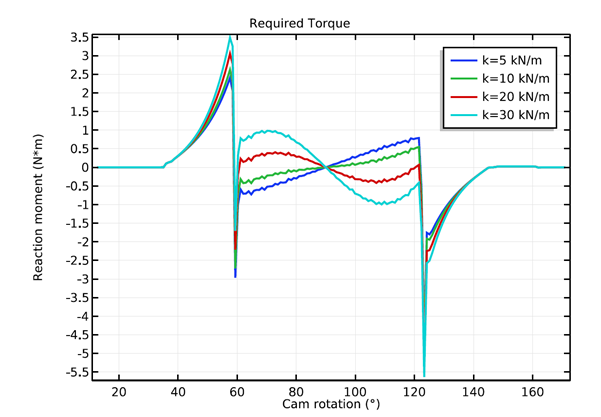
对于不同的阀门弹簧刚度值,凸轮从动件连接力随凸轮旋转(左)和旋转凸轮轴(右)所需的扭矩而变化。
在四个阀门刚度值中,只有 20kN/m 和 30kN/m 可以强制凸轮和从动件之间的连续接触。为了选择阀门刚度的最佳值,我们可以查看所需的扭矩图。在该图中可以观察到,对于 20kN/m 的值,所需的扭矩较小,因此这是本分析中考虑的值中阀门刚度的最佳值。
使用已知的从动上升函数设计凸轮轮廓
凸轮设计的一个问题是确定适合产生所需从动件运动的凸轮轮廓。在 COMSOL Multiphysics 中,可以根据随动上升函数轻松创建几何形状。从动件上升函数被定义为从动件随凸轮旋转变化的位移。第一步是导出半径作为从动上升函数。如果从动上升函数是已知的,那么可以使用分析方法建立这种关系。由于从动上升函数通常是不同基本函数的组合,因此解析法比图形法创建凸轮平面要简单得多。此外,在少数情况下,从动件的期望输出运动是已知的,因此从已知的从动件上升函数生成凸轮轮廓变得简单。
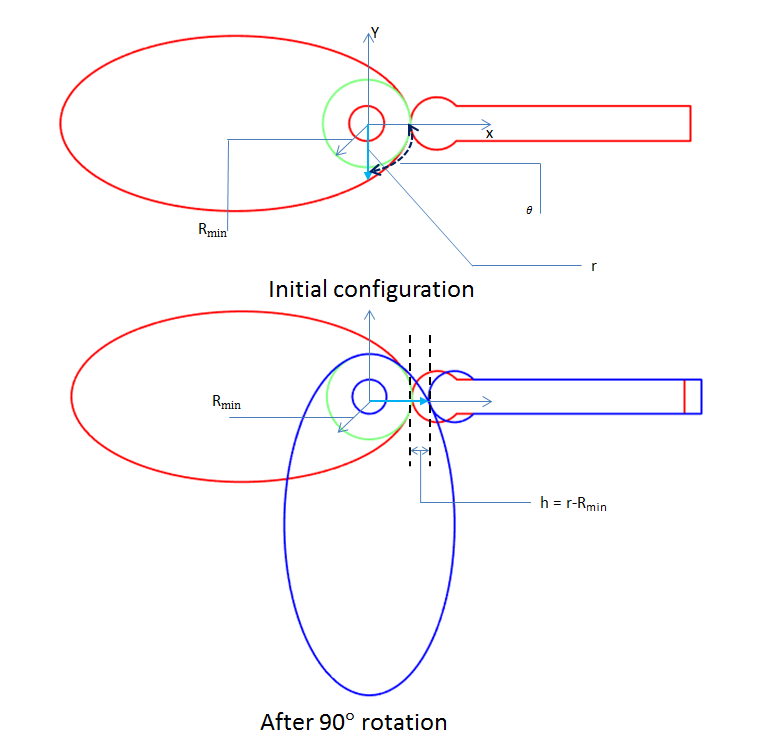
凸轮轮廓随凸轮角度变化的示意图。
- Rmin= 基圆半径
- θ= 凸轮表面上的点的旋转角度
- r= 凸轮表面上点的半径
- h= 从动件在其初始位置上方的高度
从上图可以清楚地看出,半径 (r) 和从动件高度 (h) 是旋转角度的函数,而从动件上升函数只是凸轮轮廓与基圆的差异。它们之间的关系定义如下:
现在,如果从动上升函数已知,半径 (r)的变化将代表每个θ值的圆。因此,它将给出一系列曲线。为了生成凸轮轮廓,我们需要绘制曲线的包络线。这可以在 COMSOL Multiphysics 中使用参数化曲线选项轻松完成。
y=r\boldsymbol{\cdot}
sin(\theta)
我们举一个简单的例子来说明这个概念。考虑一个简单的刀口径向从动件,其具有已知的从动件上升和凸轮角度旋转。上升函数是这样的,即在凸轮旋转 60° 期间有外行程,在凸轮旋转下一个 30° 期间暂停,在凸轮旋转下一个 60° 期间回程,以及凸轮旋转剩余的 210° 期间暂停。
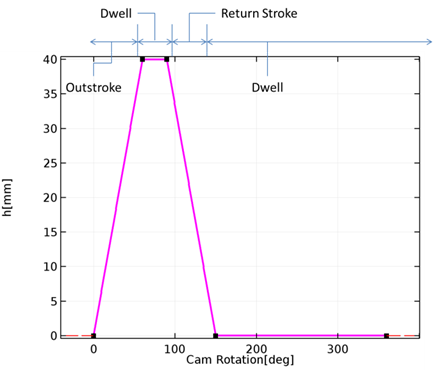
从动件高度是凸轮角度的函数。(从动上升函数。)
在 COMSOL Multiphysics® 中创建凸轮几何
首先,我们需要创建插值函数并输入 h 与θ的数据,也称为从动件上升函数。得益于 COMSOL® 软件的灵活性,我们可以直接导入随动上升函数。导入随动上升函数后,可以使用参数化曲线生成凸轮曲面。为此,需要先确定基圆半径,然后根据从动上升函数和基圆半径来表达半径。参数形式类似于圆;在这种情况下唯一的区别是半径是θ的函数。如果要在 COMSOL Multiphysics 中实现这一点,可以使用插值函数创建从动上升函数,并在参数化曲线下进一步使用它们来定义r的值(凸轮表面的半径)。通常,数据是分段曲线,因此最好为每个超行程、上行程和停顿段创建不同的轮廓曲线。最后,使用转换为实体选项生成凸轮轮廓。

生成的凸轮轮廓示意图。
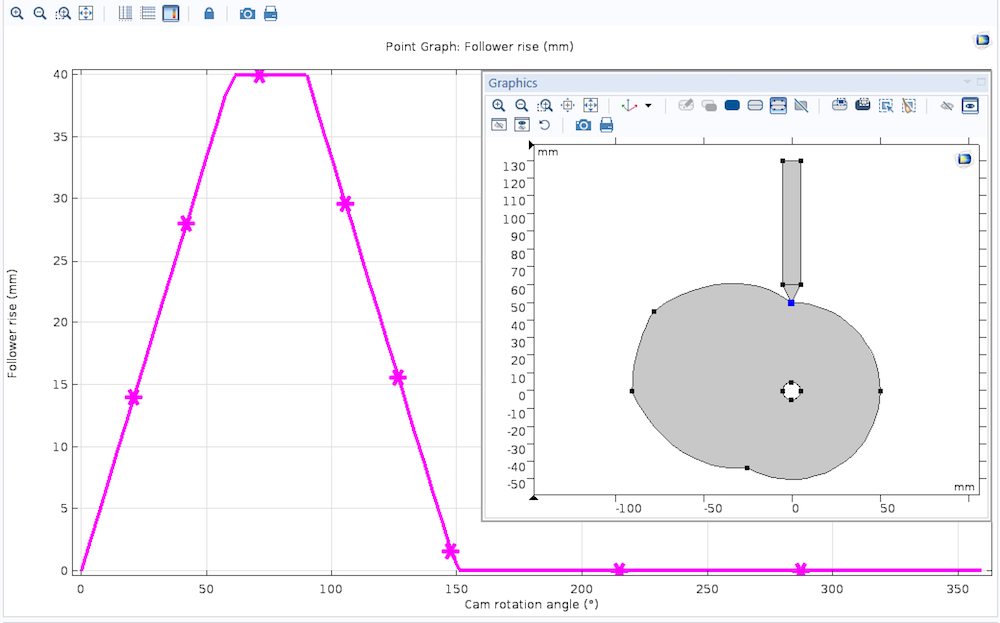
在使用生成的凸轮轮廓进行模拟后,从动件上升作为凸轮旋转的函数的图。
从动件的运动也可以是不同类型解析表达式的组合,如匀速运动、抛物线运动、简谐运动、摆线运动或一般多项式运动。在这些情况下,可以使用解析函数特征轻松创建凸轮轮廓,并结合不同的运动来实现完整的凸轮旋转。解析函数允许符号表达式,因此我们可以直接将其写为θ的函数。
使用 COMSOL Multiphysics 实现建模的最终说明
为了获得更平滑的表面,将位移的形函数阶数增加为二次是有用的。这在凸轮是刚性和柔性时都适用。
如果可能,请在凸轮边界上使用精细网格,以提高凸轮从动件连接节点中使用的网格法线的精度。
下一步
结构力学模块包含用于力学分析的高级工具。点击下面的按钮,看看还有可以进行哪些其他类型的分析。
注意:使用凸轮从动件特征还需要多体动力学模块,这是结构力学模块的附加组件。



评论 (0)