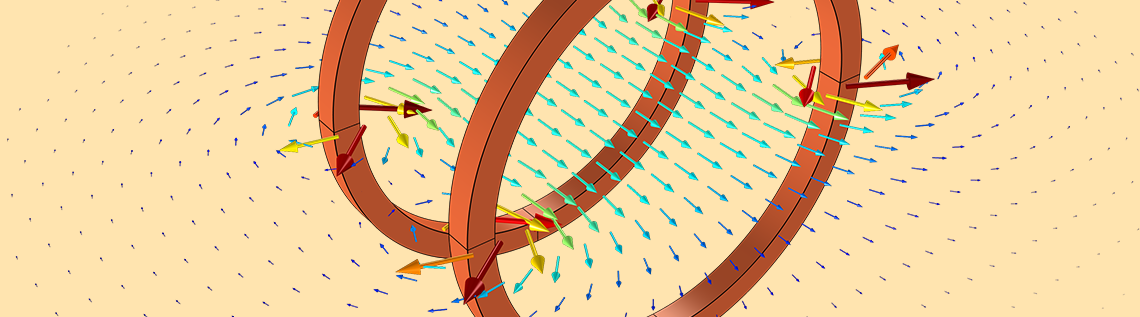
您是否曾希望查看任意几何子区域内的模型结果?您可能会认为这需要在模型中添加几何并重新计算解。而在 COMSOL Multiphysics® 软件中,用户可以仅仅只是通过添加零件并调整其位置,来达到估算结果的目的。我们将以计算线圈互感系数为例来演示具体的操作,并介绍一些简单而有用的技巧。
计算互感系数
让我们先来看看下图中两个圆形载流线圈模型,其载流电流均为 I0= 0.25 mA。绘图显示了两个初级线圈周围的磁通密度,即B场。假设我们要在较大的初级线圈之间添加一个相对较小的拾波线圈。这个拾波线圈会拦截一部分磁,它通过其外周曲线C和封闭区域A来定义。
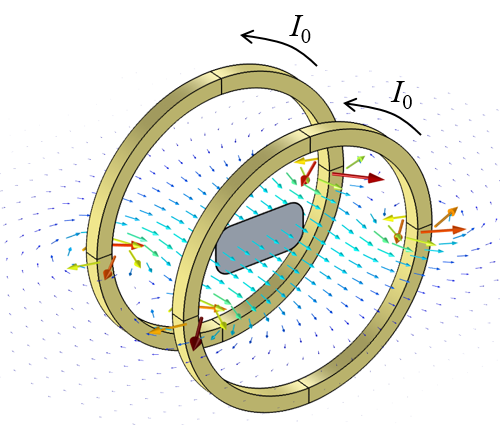
内部放置了拾波线圈的亥姆霍兹线圈周围的磁通密度。线圈的封闭区域显示为灰色阴影。我们将重新计算拾波线圈改变方向后的互感系数。
初级线圈和拾波线圈之间的互感系数可定义为:
其中n表示垂直于表面A的矢量。
由于B场是基于磁矢量势\mathbf{B=\nabla \times A}计算出来的,所以根据斯托克斯定理,上方的面积分应等于线积分:
其中t表示与曲线C相切的向量。
官网“案例下载”中的射频识别系统案例也采用了这种互感系数的计算方法。
我们可以将拾波线圈放置在初级线圈四周的任意位置和方向上,然后对模型进行求解,计算出其中一种积分。我们甚至可以在使用更新解功能对模型进行求解后,再添加拾波线圈几何特征。这项功能可以重新剖分整个模型几何的网格,并将之前计算的解从旧网格映射到新网格上。如果几何的变化不会影响解,而且只是需要在不同的位置上求解拾波线圈,那么这种方法既适用又非常方便。
假设我们计划将拾波线圈放置在各种不同的位置和方向上。考虑到A场不变,所以我们不希望对整个模型进行重新求解或网格剖分,只想移动拾波线圈的几何。为了实现这一需求,我们可以使用多个几何组件的组合,即广义拉伸组件耦合和积分组件耦合。
在 COMSOL Multiphysics® 中的任意几何上积分
我们从现成的亥姆霍兹线圈为例,向模型中添加一个新的三维元件。第二个元件的几何可用于定义拾波线圈的边、横截面和方向。借助旋转和移动几何特征,我们能将线圈调整为任意位置。为了方便可视化,我们还可以添加专用于定义初级线圈的边,如下方截图所示。
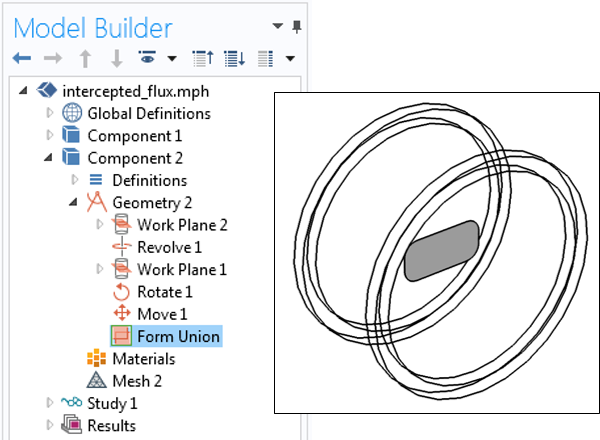
第二个组件和几何的设置。
Component 2的空间坐标与Component 1完全重叠,但除此之外,二者之间没有任何联系。通过定义在Component 1中的“广义拉伸”组件耦合,我们引入了映射。此耦合将Component 1的全部域列入了源选择。无论在Component 2空间中的哪一点上计算此耦合,Component 1空间中都会使用同一点上的场。
“轴模型的子模型分析”教学模型也介绍了如何使用两个组件及在二者之间映射解的具体方法。
在Component 2中,我们定义了两个“积分”组件耦合,一个定义在拾波线圈的边上,名为intC,另一个定义在横截面边界上,名为intA。借助两个组件耦合,我们可以通过定义两个变量,从而采用上述任一方法来计算互感系数。两个变量分别名为L_C和L_A,其定义公式分别为:
intC(t1x*comp1.genext1(comp1.Ax)+t1y*comp1.genext1(comp1.Ay)+t1z*comp1.genext1(comp1.Az))/I0
和
intA(nx*comp1.genext1(comp1.mf.Bx)+ny*comp1.genext1(comp1.mf.By)+nz*comp1.genext1(comp1.mf.Bz))/I0
其中,t1、t1y 和 t1z为拾波线圈周长的切矢分量,nx、ny 和 nz 为拾波线圈表面的法矢分量;I0= 0.25 mA 是一个全局参数。
由于模型包含了多个组件,所以我们必须使用Component 1中的组件耦合和场的完整名称。另外请注意:法矢和周长切矢的方向可能相反,我们需要注意正负号的改变。
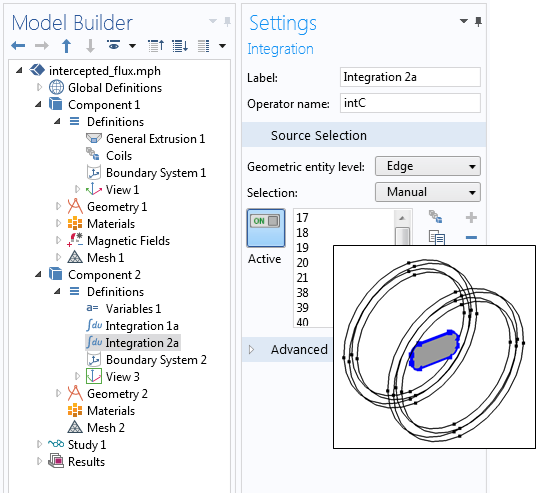
定义在第二个组件的拾波线圈周长上的“积分”组件耦合。
我们还能对不同位置和方向上的拾波线圈执行扫描。在Study 1中,我们已对磁场进行了求解,现在添加第二个研究,使之包含参数化扫描,但没有求解任何物理场。在研究步骤设置中,我们可以指定使用现有的磁场求解结果,如下方截图所示。
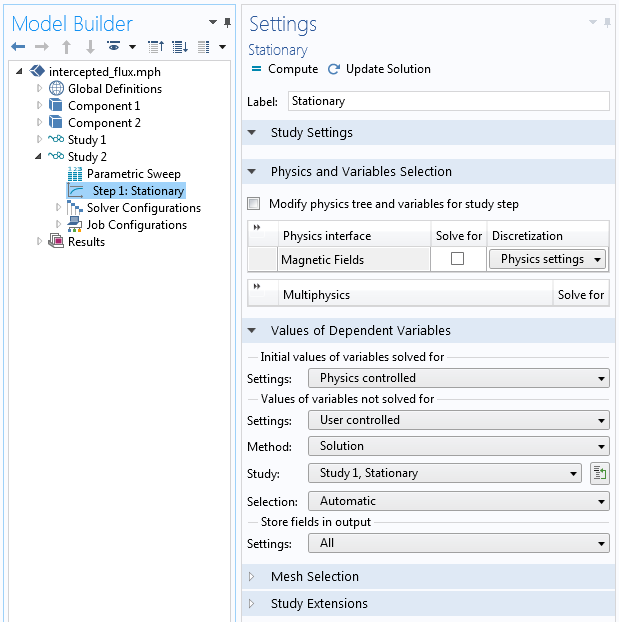
研究步骤设置显示了如何将Study 1的解应用到Study 2中。
相比于重新剖分整个模型网格并求解磁场,第二个研究的计算量更小。拾波线圈每一次改变位置,软件都只会剖分拾波线圈表面的网格,然后将Study 1的解映射到拾波线圈的新位置上,并对两个变量进行求解。
这种方法同样适用于空间积分表面和多匝积分曲线,射频识别系统便是一个符合的案例。不仅可以在任意的边和表面上进行积分,还能通过旋转和移动几何操作轻松地调整到任何位置上。综上所述,它一个计算任意几何和位置上的场的常用方法。
一个更加简单的方法:使用截面
上述方法十分灵活,支持对任意形状进行积分。下面,我们将讨论一个相对简单的例子。假设我们要处理平面积分表面,该表面的边可以参照平面上的原点简单地使用x坐标和y坐标来定义。
该方法的第一步是在整个建模空间中建立一个切面(截面)。我们可以使用截面数据集来完成这一步,详情可参考关于计算平面上的总法向通量的博客文章。我们可以使用全局参数来设置截面的原点和法矢。另外请注意:我们在截面上分别定义了局部变量cpl1x和cpl1y来表示局部的x和y位置,并定义了cpl1nx、cpl1ny和cpl1nz来表示平面法矢的分量。
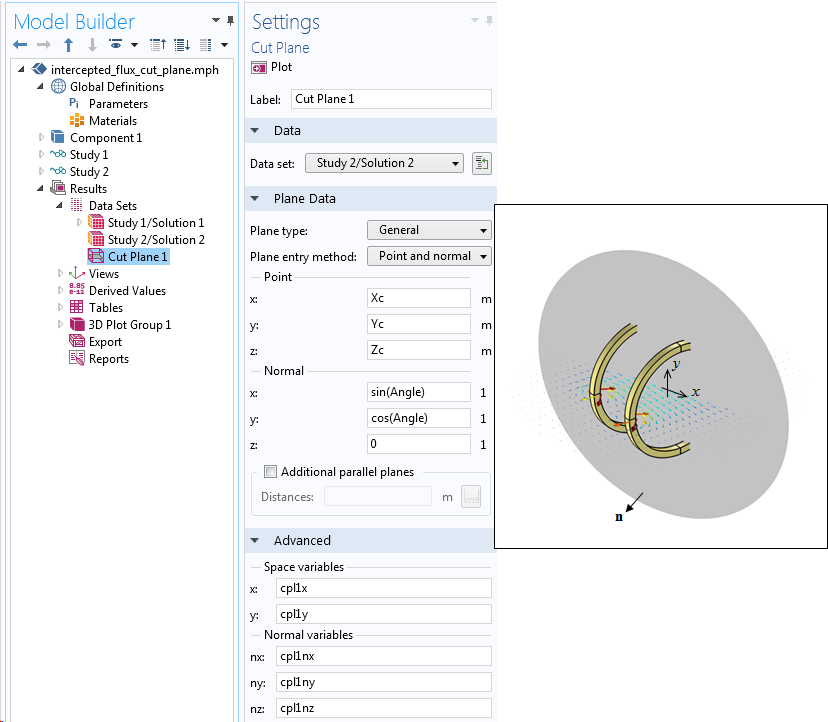
使用“截面”数据集。原点和法向是利用全局参数来定义的。高级设置显示了局部的x和y坐标以及法向坐标的名称。
接下来,我们将在整个截面上进行表面积分,但同时希望将积分对象限定为平面上的一个子空间。为此,我们使用了与空间相关的逻辑表达式,在待求解的区域内,表达式的值为 true(或 1),反之为 false(或 0)。然后,用逻辑表达式乘以被积函数。举例来说,如下方截图所示,在截面上进行的表面积分是一个表达式:
-(sqrt(cpl1x^2+cpl1y^2)<0.1[m])*(cpl1nx*mf.Bx+cpl1ny*mf.By+cpl1nz*mf.Bz)/I0
其中,以原点为中心、半径为 0.1 米的圆内,逻辑表达式(sqrt(cpl1x^2+cpl1y^2)<0.1[m])的值为 1。
表达式中其余的项计算了通量与截面法矢的乘积,最终得到了以截面原点为中心、半径为 0.1 米的圆中通过的通量。
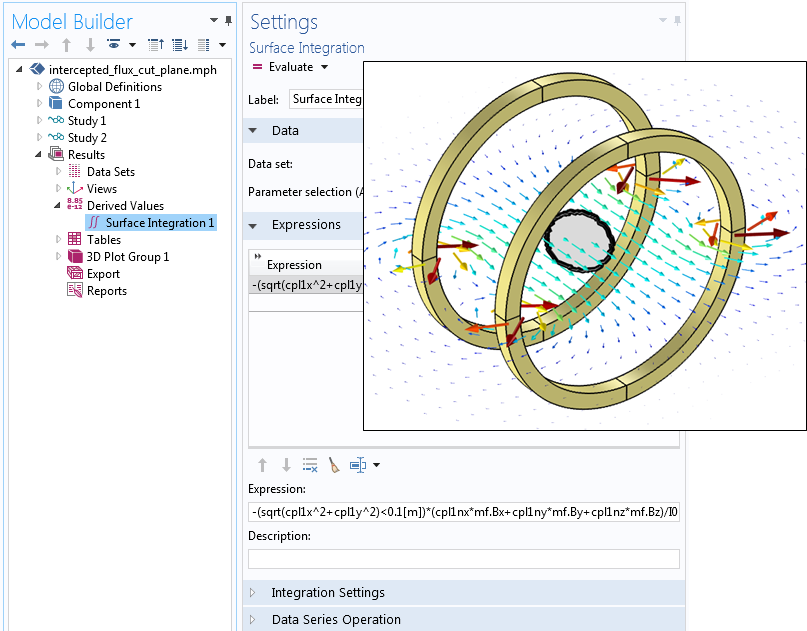
使用逻辑表达式计算截面子区域上的积分。
截面子区域的边界略微不平滑;不过随着网格逐渐细化,粗糙度会降低。与上文的方法一样,我们借助第二个包含参数化扫描的研究,将所有不同方向的截面存储在第二个数据集中。由此,我们不需要建立第二个组件或几何,免去了重新定位和重新剖分网格的麻烦,从而加快了计算速度。
一个更简单的方法:使用参数化曲线
下面,我们将介绍一个更加简单的方法,它所适用的情况相对较少。假设我们要对可通过参数方程描述的曲线进行积分。可通过参数方程描述的最简单曲线之一是 xy 平面上的单位圆,其定义为x=cos(s), y=sin(s),区间为0\le s \le 2\pi。计算任何参数曲线的切矢的方法简单又直接。单位圆的切矢分量如下:
\textless \text
{tx,ty}
\textgreater = \textless-sin(s),cos(s) \textgreater
我们可以在三维参数化曲线数据集中使用这些简单方程,以求解 xz 平面内半径为 0.1 米的圆。通过使用一组全局参数,圆的中心点会从全局原点偏移开。
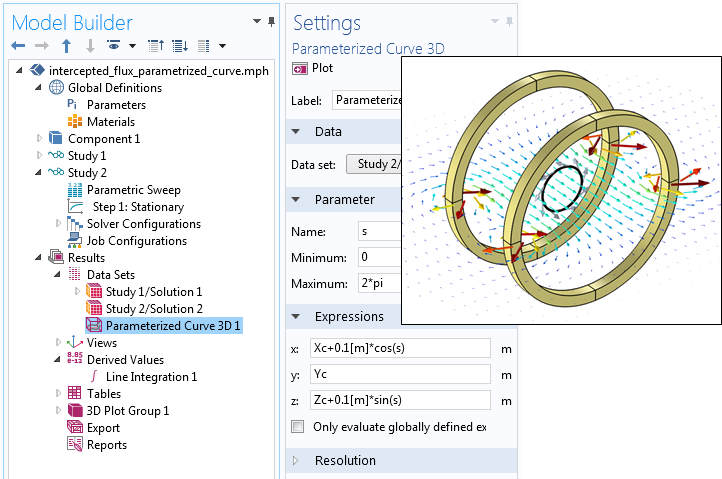
“三维参数化曲线”数据集的设置。曲线显示为黑色,切矢箭头显示为灰色。
我们可以基于另一个研究创建第二个数据集,并利用参数化扫描对拥有不同原点的圆进行计算。然后,我们对新的数据集进行线积分,如下方截图所示。被积函数
(-sin(s)*Ax+0*Ay+cos(s)*Az)/I0
在 xz 平面上假设了一个圆,并沿参数曲线计算出A场。
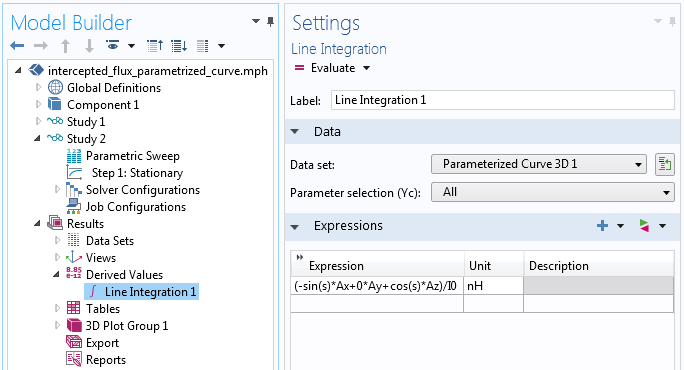
对“参数化曲线”数据集进行线积分。
针对给定的网格离散化,第三种方法最简单且最准确,但限制也最多。圆、椭圆和正方形之外的曲线不与坐标轴对齐,因此写入它们的参数方程的难度更高。
在下图中,我们采用了三种方法计算沿线圈的轴往复移动的圆形积分区域,绘制并比较了三者的结果。
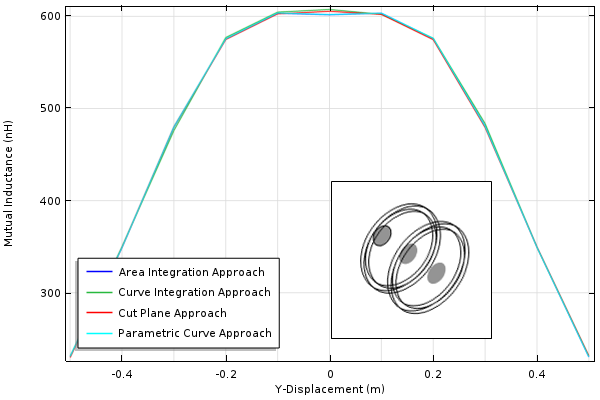
比较各种计算互感的方法。
关于对任意几何的场进行后处理的结语
在上文中,我们展示了三种提取建模空间内子区域的表面和线积分的方法。第一种方法最通用;它允许对任意(甚至是非平面)表面和曲线进行积分,还支持任意改变待求解积分的几何的位置。这种方法最为灵活,但是前期准备工作也是最多的。
第二种方法(使用“截面”数据集)仅适用于平面积分表面,而且在积分表面的形状方面受到了诸多限制。第三种方法(使用参数化曲线)最高效简单,但是最适用于诸如圆之类的简单积分曲线。
更多资源
- 阅读“COMSOL 博客”中关于子区域积分的文章
- 阅读下列博客文章,学习如何使用“广义拉伸”组件耦合:



评论 (0)