COMSOL 博客

非线性弹性材料简介

2015年 1月 9日

非线性弹性材料即使在极小的应变下也呈现非线性的应力-应变关系，这与超弹性材料相反，后者的应力-应变曲线在中到大应变下变得明显非线性。这一类重要材料包括用于模拟金属和其他韧性材料的 Ramberg-Osgood 模型，以及非线性土壤模型，例如 Duncan-Chang 模型。

幂律

早在 100 年前，Paul Ludwik 在他的论文Elemente der Technologischen Mechanik中对固体中的非线性应力-应变行为进行过描述。其中，Ludwik 描述了在扭转试验中观察到的剪切应力和剪切应变之间的非线性关系，也就是现在的Ludwik 定律：

(1)

\tau = \tau_0 + k\gamma^{1/n}

当n=1时，应力-应变曲线是线性的；当n=2时，曲线是抛物线；当n=\infty，曲线代表完美的塑性材料。Ludwik 仅描述了我们现在称为假塑性材料的行为(Fließkurve) 。

在 COMSOL Multiphysics 仿真软件 5.0 版本中，除了 Ludwik 幂律之外，非线性结构材料模块还包括非线性弹性家族中的不同材料模型：

Ramberg-Osgood
幂律
单轴数据
双线弹性
用户自定义

在岩土力学模块，我们现在包含了用于描述土壤非线性变形的材料模型：

双曲定律
Hardin-Drnevich
Duncan-Chang
Duncan-Selig

单轴数据示例

非线性弹性材料和弹塑性材料（金属或土壤塑性）之间的主要区别在于变形的可逆性。虽然非线性弹性固体在加载-卸载循环后会恢复到原来的形状，但弹塑性固体会出现永久变形，应力-应变曲线会呈现滞后行为和棘轮。

我们来看一个的教程模型：穿孔板的弹塑性分析。它在非线性结构材料模型库中以elastoplastic_plate的形式提供，我们对它进行修改来求解一个加载-卸载循环。我们还添加了 5.0 版本软件中包含的一个新材料模型，即单轴数据模型，并使用模型中已经定义的 stress_strain_curve。

以下是这些选项的屏幕截图：

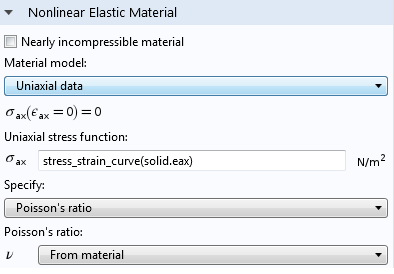
非线性弹性材料简介

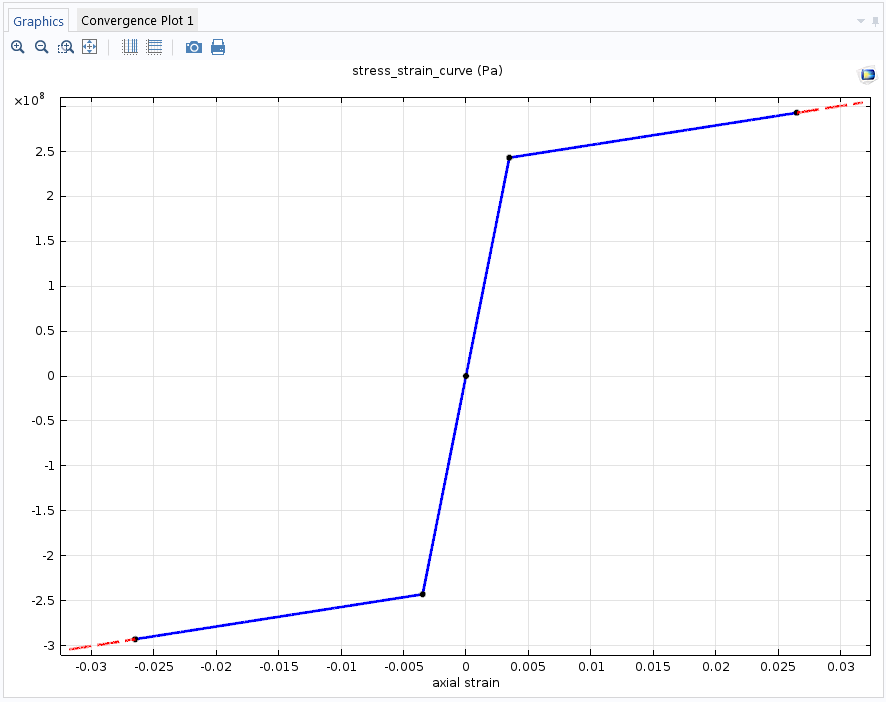
在这个示例中，stress_strain_curve 表示作为轴向应变函数的轴向应力的双线性响应，当n=1时，可以从 Ludwik 定律中恢复。

描述了应力-应变曲线的绘图。

我们可以比较将板横向加载到最大值后的应力分布。结果几乎相同，主要区别在一个完整的加载-卸载循环之后被观察到。

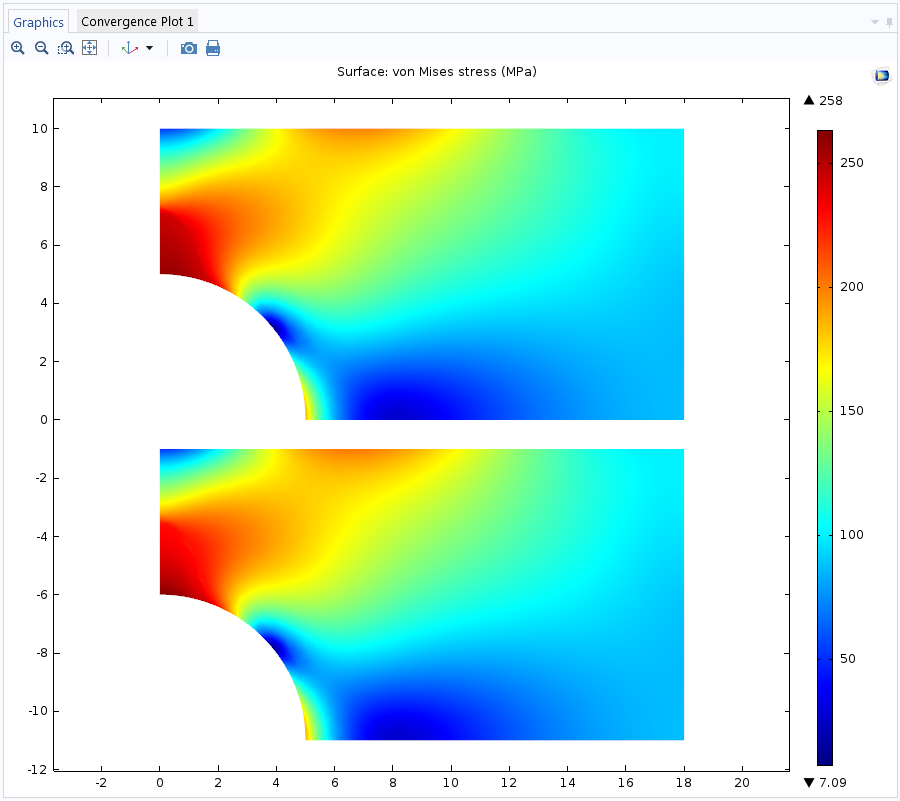
应力分布的比较。
顶部：弹塑性材料。底部：单轴数据模型。

选择观察到的最高应力的点，绘制x方向应力分量与相应应变的关系。绿色曲线显示了应力和应变之间的非线性但弹性的关系（应力路径从a\rightarrow b \rightarrow a \rightarrow c \rightarrow a）。蓝色曲线描绘了在具有各向同性硬化的弹塑性材料中观察到的滞回循环（应力路径从a\rightarrow b \rightarrow d \rightarrow e)。

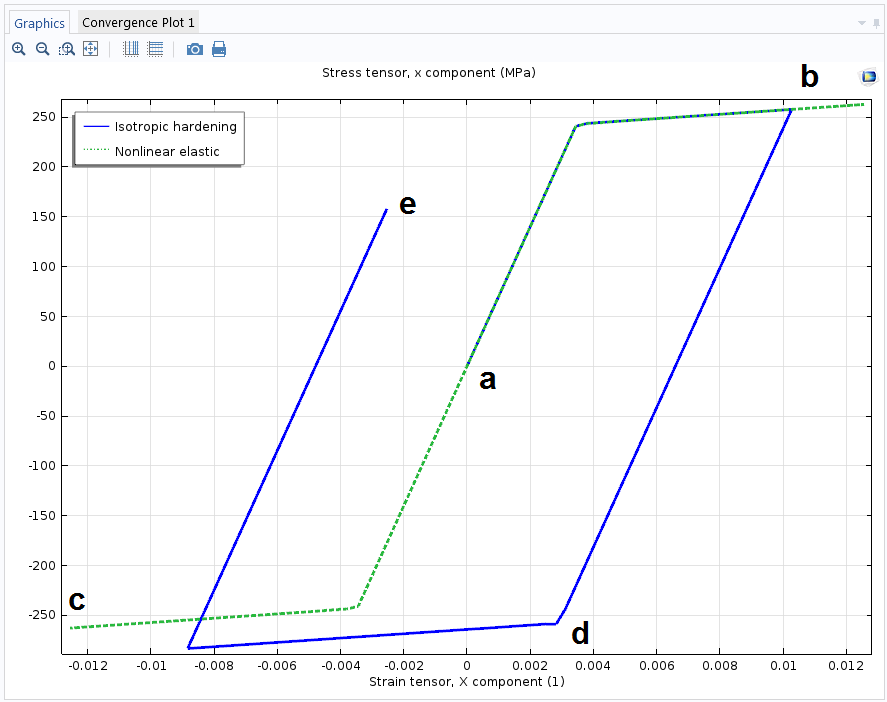
一个滞回曲线绘图。