
你有没有想过,模型几何的拓扑结构,换句话说,将几何体分解为域、边界、边和顶点等几何实体,是否会在某种程度上影响COMSOL Multiphysics®软件中网格生成对计算资源的使用?如果是这样,那么你可能会对本篇博客感兴趣……
COMSOL Multiphysics®中的并行网格划分
以下操作使用共享内存的并行:
- 自由四面体网格
- 自由三角形网格
- 自由四边形网格
- 映射
- 边界层
- 扫掠
自由四面体是跨域和面的并行操作。这意味着当此操作在一个具有四个域的几何上生成四面体时,它最多可以使用四个内核,而如果几何中有一个域,则相同的操作只能使用一个内核——不管有多少个内核可用。类似地,自由三角形、自由四边形和映射操作在二维域和三维面之间是并行的。
边界层操作是部分并行的。与其他操作不同,这个网格操作在每个域内是并行的。
最后,作为扫描操作的一部分,连接面的网格划分(通过映射操作完成)是并行的。
请注意,在网格操作的序列中,网格的建立是自上而下,一次一个操作。因此并行化是在每个操作中一次完成的。
基准示例性能测试
在实际建模场景中,并行化的网格划分能加快多少时间呢?我们取一个 6m×1m×1m的块,在一台有 6 个内核的普通台式电脑上进行网格划分。在网格下添加一个自由四面体操作。在整个测试过程中,使用以下网格单元大小参数。
- 最大单元大小:
0.02 m - 最小单元大小:
0.01 m
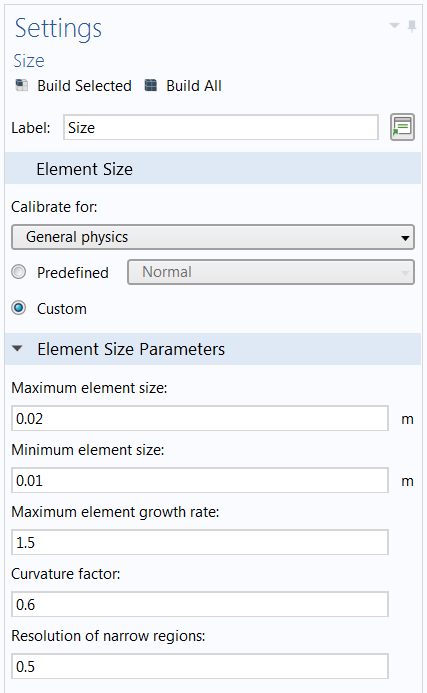
基准示例测试中使用网格的大小设置。
这些设置提供了非常精细的网格,从而产生了大约 1300 万个四面体单元。
我们设置了三个测试示例,其中的模型分别具有:
- 一个域
- 六个域,将块划分为六个大小相等的域
- 六个域,限制软件只能在一个内核上运行
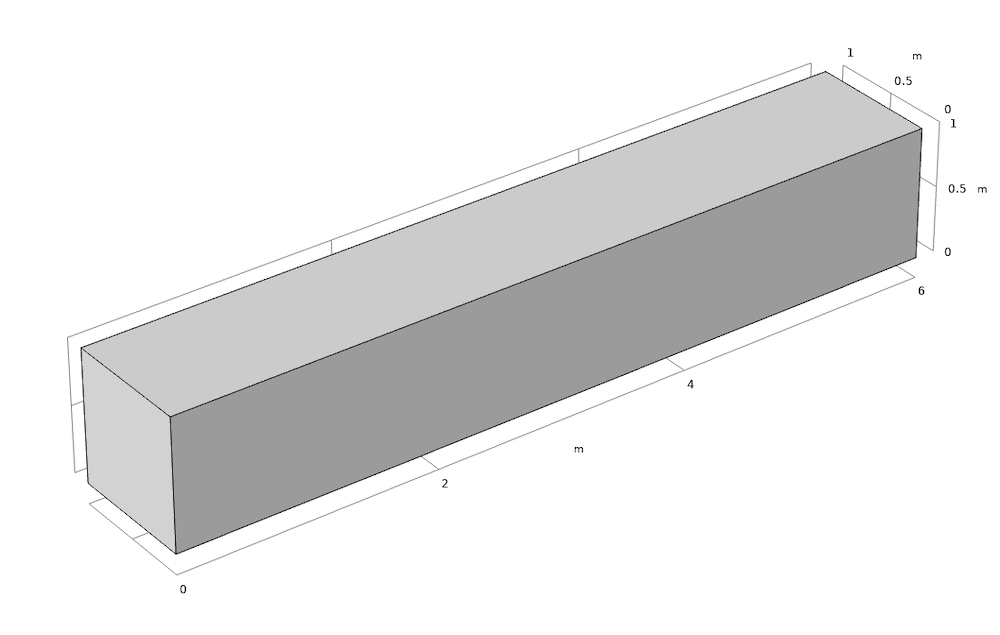
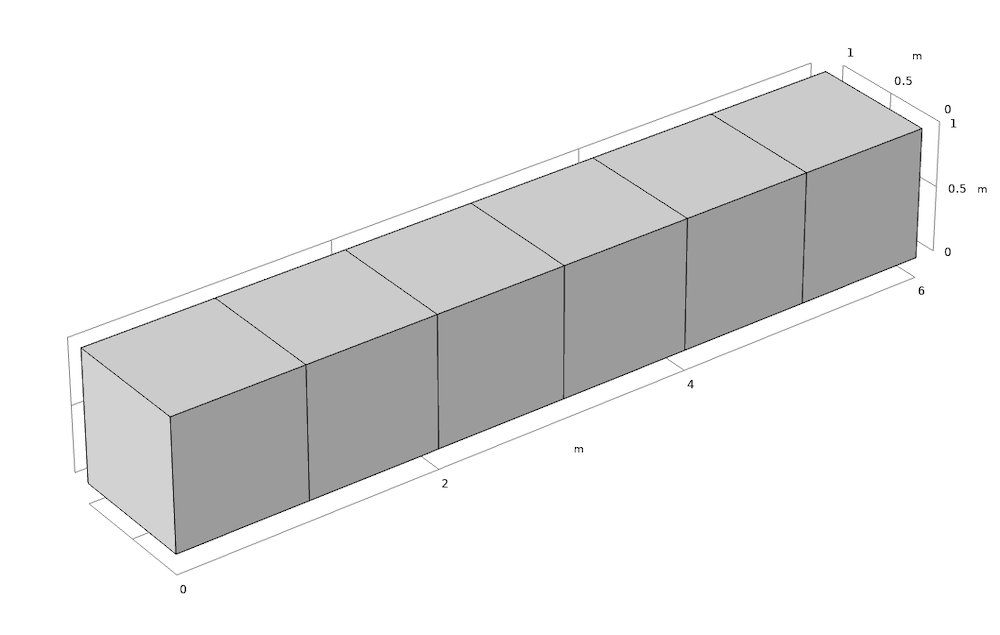
左图:具有 1 个域的 6 m×1 m×1 m 块(情况1)。右图:与情况1具有相同外部大小的几何图形,但分为6个大小为1 m×1 m×1 m的域(情况2和3)。
为了限制软件仅在一个内核上运行,可以将选项-np 1添加到启动命令。也可以在首选项对话框的多核与集群计算页面上执行此操作。
基准示例测试结果和讨论
3 次测试的结果汇总在下表中。情况 1 和 3 中的网格划分将仅在 1 个内核上运行,并且需要大约相同的时间来划分网格。含 6 个域的几何结构(情况 2 和 3)具有更多的边界,因此会产生更多的三角形单元,这也意味着该几何结构需要更多的网格划分工作。在情况 2 中,网格算法使用所有 6 个内核,但网格划分时间减少到仅使用一个内核时的 25% 以下。
| 情况 | 域 | 时间 | 三角形单元 | 四面体单元 |
|---|---|---|---|---|
| 1 | 1 | 136 s | 1.51e3 | 13.0e6 |
| 2 | 6 | 31 s | 1.81e3 | 13.0e6 |
| 3(1核) | 6 | 147 s | 1.81e3 | 13.0e6 |
在六核台式计算机上运行的基准示例测试结果。测试显示从一个核(表中的第一行和第三行)到六个核(表中的第二行)有明显的加速。
你可能想知道是否应该将几何体划分为与核一样多的域,假设开始时的域较少。答案是:没有必要…
对域进行分割会导致更多的边界。这就给网格设置了更多的约束,反过来,这可能会给网格带来更复杂的情况。边界增加将需要更长的时间进行网格划分,通过比较情况 1 和 情况3 中三角形单元的时间和数量,我们可以清楚的看到这一点。还应该考虑到,分割域会导致需要更精细网格大小的狭窄域。请注意,这个基准示例中的情况是理想化的,即六个核上有六个相等的域。在实际情况下,更有可能的是一些域更复杂,并主导了网格划分的时间,从而导致速度降低。
使用边界层划分域
边界层操作在插入边界层单元时是平行移动点的,甚至在单个域上操作也可以这样做。因此,分割域不会提高性能,相反,因为额外的分割面需要更多的处理时间。
我可以使用多少个网格操作而不损失性能?
我们使用上面基准示例中的情况2(在最多六个核上进行六个域的网格化)来说明。并行化是按网格操作进行的,因此如果我们现在再添加另一个自由四面体操作,并在每个操作中对三个域进行网格划分,则最多可以使用三个核。一般来说,建议使用尽可能少的网格操作(相同类型)。这不仅可以尽可能的并行化,而且还可以很好地优化网格的质量。要在不同的域或边界上设置不同的尺寸,请使用多个全局或局部尺寸属性,并且只使用一个自由四面体操作。使用网格划分序列教程模型中讨论了有关设置全局和局部尺寸属性的细节。
网格划分并行运行的总结性思考
在这篇博客中,我们讨论了 COMSOL Multiphysics 中网格划分算法的并行化方式。一个简单的基准示例测试结果表明,并行运行的网格划分可以通过将域的网格分布在更多核上来明显加快算法速度。
推荐阅读
有关自由四面体操作的更多信息,以及修改几何的可能方法,请查看以下资源:



评论 (0)