如何在 COMSOL Multiphysics 中合并解

在工程分析中，经常需要比较在不同工况下获得的解。可能包括比较不同载荷或参数配置的影响，以及在域的每个点上对解进行包络以找到最差或最佳的情况。对于上述每一种情况以及其他类似情况，我们都需要访问多个数据集。下面，我们将介绍使用 COMSOL Multiphysics 完成这些任务的方法。

COMSOL Multiphysics 中的合并特征

在 COMSOL 中合并解，需要右键单击结果下的数据集，然后选择合并。当使用功能区（如果正在运行 Mac^®OS 或 Linux^®，则使用菜单）时，命令为结果> 更多数据集> 基数据集 > 合并。在合并设置窗口中，我们需要做出两个选择：组合哪些解，以及如何组合它们。

我们可以在数据1和数据2中确定基础数据集。在数据2的正下方，可以配置组合方法。

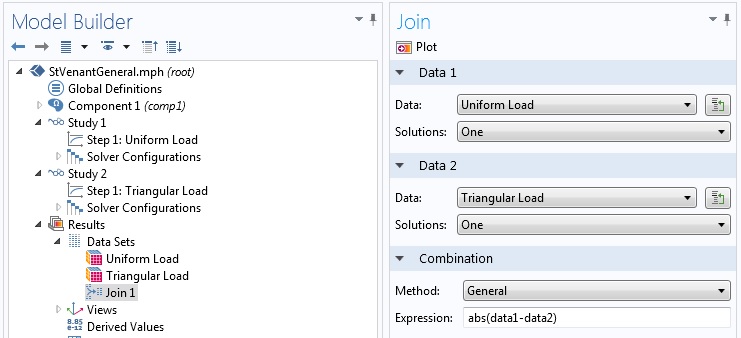
合并设置窗口。

组合方法有 7 种选择，我们可以将其中的 5 种作为另外2种选项的特例。下面我们将讨论常规和显式2种方法。

常规合并方法

当方法被设置为常规时，会出现一个字段，我们可以在其中输入表达式。例如，data1-data2是一个差异表达式，(data1-data2)^2是差异的平方。后者可以用作评估 L2 模差的平方。

在此阶段，未指定要比较的变量。实际上，我们正在构造一个算子，该算子可用于两个原始基本解中定义的任何变量。接下来，我们以一个T为因变量的问题为例来说明，如传热问题。

假设我们在表达式字段的合并设置窗口中输入(data1-data2)^2，并将新数据集命名为Join 1。为了绘制温度差的平方，在绘图设置窗口中为数据集选择Join 1，并选择T作为表达式。

为了演示如何使用常规方法进行解合并，下面我们通过两个模型示例来说明。

示例1：绝对差

在此示例中，通过一个沿右端均匀分布的 10 MN/m 的载荷和一个同一个边缘在中心最大强度为 20 MN/m，末端为0 MN/m 的三角载荷交替加载一个厚度为 0.1 m 的膜的二维平面应力模型。这两个载荷在静态上是等效的。根据圣维南原理，离载荷的边缘越远时，解的差异就越小。

首先，我们使用均匀载荷进行计算，然后使用三角载荷来计算得到两个稳态解。如上图所示，方法选择常规，并在表达式栏中输入abs(data1-data2)创建一个合并解Join 1。为了绘制 von Mises 应力中的绝对差，使用 Join 1 数据集绘图并在表面图设置窗口的表达式栏中输入solid.mises绘制表面图。在下图中，如圣维南原理所预测，von Mises 应力在载荷边缘附近差异很大，而在远离边缘的地方差异很小。

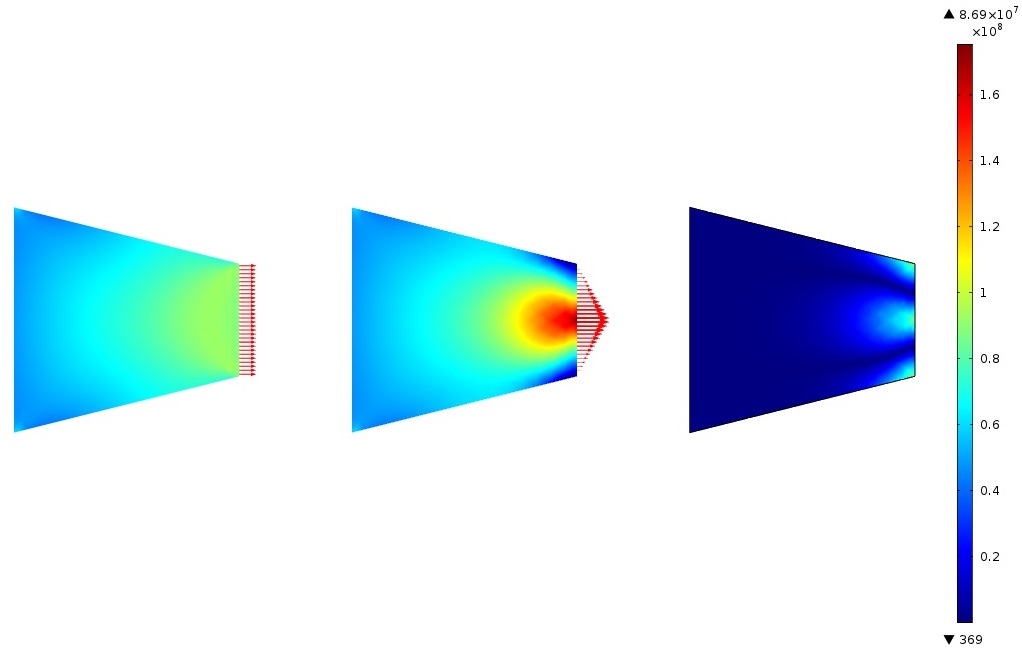
具有均匀和三角形边界载荷的 Von Mises 应力，以及 Von Mises 应力的绝对差。

示例 2：结果包络

通常，工程师会针对不同的运行条件进行分析，并希望了解该域中所有点的最佳或最差情况。例如，在热分析中，通常对最高温度比较关注。域中的某些点，在某一种工况下达到最高温度，而其他点则在另外的工况下达到最高温度。温度包络显示了在多种可能的工况下每个点的极端温度值。

对于此示例，我们考虑一个简单的稳态一维热传导问题。在第一种情况下，左端温度为 300 K， 右端温度为 400 K。在第二种情况下，温度发生反转，左端温度为 400 K，右端温度为 300 K。

为了构建最大温度包络，我们使用常规方法和max(data1,data2)表达式从两个解中创建一个合并数据集 Join 1 。然后，在线图中，数据集选择Join 1，表达式选择T,以获取最大温度包络（如下所示）。

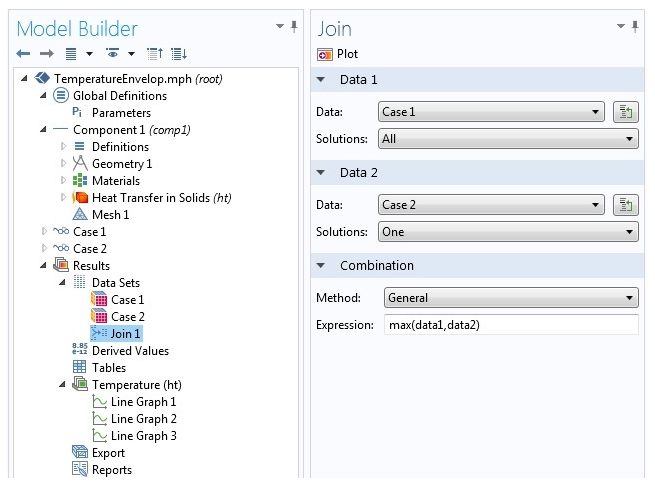
结果包络设置。

在下图中，我们可以看到合并操作和结果包络以及两种基本情况的结果：

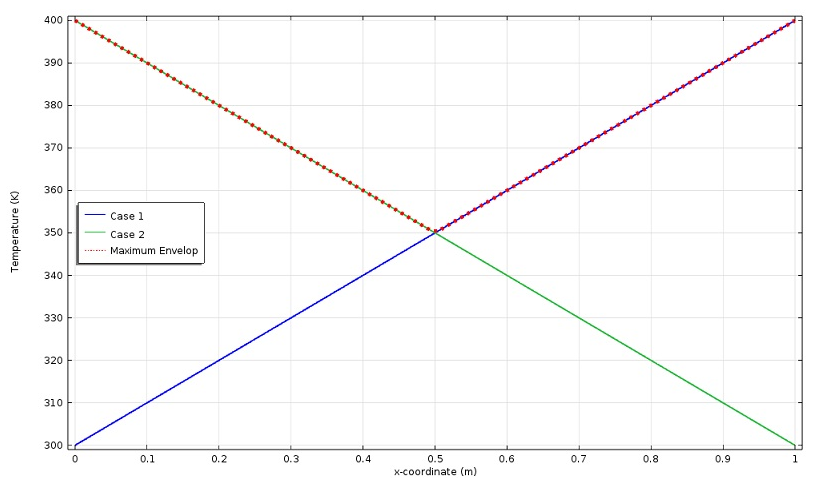
如果要绘制最小温度包络，则必须使用 “合并设置”窗口中的min(data1,data2)添加一个新的合并数据集。

显式合并方法

使用常规方法进行合并时有一个限制，即在后续操作（例如绘图或积分）中，必须使用两个基本解中的相同变量。例如，要绘制第一个数据集的变量u和第二个数据集的变量v之和，就不能使用常规方法。如果在合并设置窗口的表达式下有data1 + data2，则可以将其与u一起使用，返回data1(u) + data2(u)；或者和v一起使用，返回data1(v) + data2(v)。

这时就可以使用显式方法。选择此方法时，COMSOL Multiphysics 会创建两个新的算子 data1 和 data2，可分别用于访问第一个和第二个数据集中的量。与常规方法不同，显式方法在解合并阶段没有用于键入表达式的字段，我们可以在后面的绘图、积分、平均值或其他设置时直接使用这两个算子。例如，data1(u) + data2(v)可以在绘图设置窗口中键入，前提是u是第一个解中的合法变量，并且v在第二个解中可用。

显式方法的另一个优点是，由于表达式在解合并阶段不是固定的，因此我们无需创建新的合并数据集就可以使用其他表达式。例如，在一维传热问题中，我们可以进行显式合并，并将其用于 L2 和 H1 模的两个不同的线积分中。对于 L2 模，我们将使用(data1(T)-data2(T))^2；对于 H1 模，我们将使用(data1(T)-data2(T))^2 + (data1(d(T,x))-data2(d(T,x)))^2。此处，d（T，x）是T相对于的x的导数，它是 COMSOL Multiphysics 中的预定义算子。

回到温度包络示例。使用常规方法绘制最大和最小温度包络时，我们需要两个合并数据集。如果改用显式方法，则只需要一个合并数据集，并使用max(data1(T),data2(T))和min(data1(T),data2(T))在线图中分别绘制最大和最小包络。

在合并数据集上使用算子

常规方法

我们可以在模型开发器的定义节点中添加函数和组件耦合算子。如上所述，使用常规方法时，我们还会得到一个算子。因此，当我们使用用户定义的耦合算子或函数，并使用常规方法合并数据集时，最终得到了一个复合算子。问题是：组合中的哪个算子是内部算子，哪个是外部算子？答案是，通过解合并生成的算子是外部算子，并且在定义节点中添加的任何算子都将成为内部算子。下面我们用一个例子来说明这一点。

以在上述一维热传导示例的定义节点中添加的耦合算子intop1为例。数据集 Join 2 是由使用通用方法和表达式(data1 - data2)^2的两个解组成。如果我们选择 Join 2 作为数据集，intop1(T)作为结果 > 派生值> 全局计算中的表达式 ，是否能够得到两个基本解之差的L2-模呢？答案是：不能。全局计算返回零值。

由于intop1是内部算子，因此要评估的是(intop1(T)-intop2(T))^2，这显然不是差的 L2 模。要获得差的 L2 模，我们必须使用结果> 派生值中可用的预定义积分算子，然后为数据集选择Join 2并选择我们的域。最后，使用T作为 Expression。下图显示了使用 COMSOL Multiphysics 实现这些操作的过程及其数学表达式。

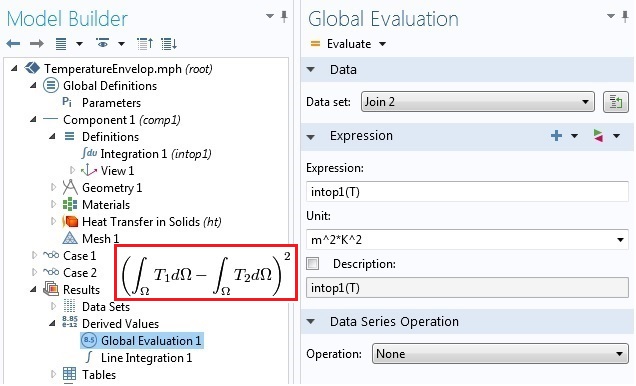
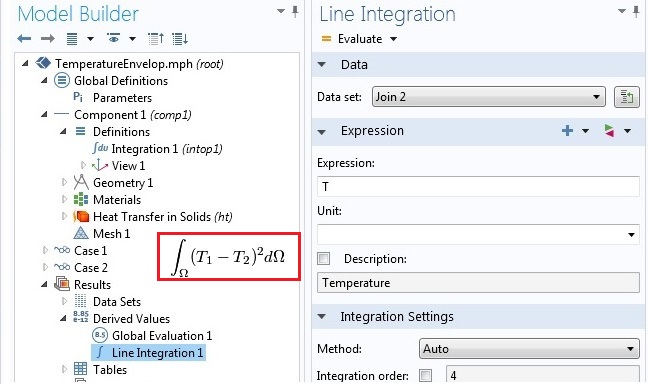
通过常规方法在合并解上使用算子。

总之，复合运算中的算子顺序如下：在定义节点中添加的函数或耦合算子；通过合并创建算子；在结果 > 派生值中从内部到外部使用预定义的平均值、最大值、最小值和积分算子。

显式方法

使用显式组合时，情况会更清楚。下图显示了如何在显式合并的数据集 Join 3 上计算积分差和差分积分。

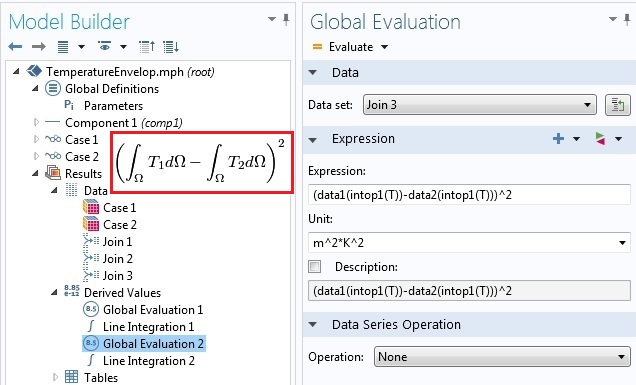
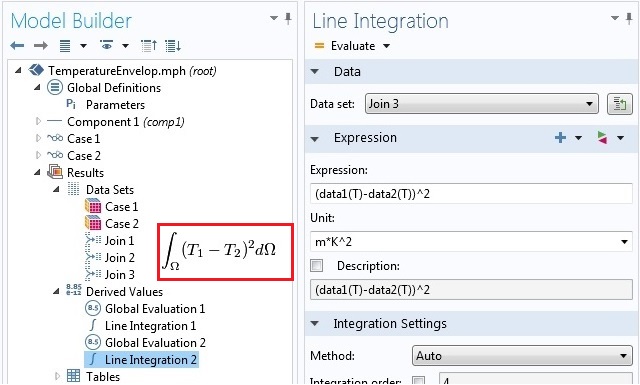
通过显式方法在合并解上使用算子。

其他合并方法

其他 5 种组合方法分别是差集、差分的模、积、商以及总和。他们等同于对常规方法使用表达式data1-data2、abs(data1-data2)、data1*data2、data1/data2和data1 + data2。当然，用常规方法做的任何事情，也可以使用显式方法完成。

在本篇博文中，我们主要讨论了无参数扫描的合并稳态解。在参数扫描或瞬态解中，每个基本解都包含多个数据集。特征频率和频域研究也是如此。对于这些研究类型，合并解可用于评估一些有用和有趣的物理量。我们将在后续博客文章中对此进行讨论。

如果需要更多帮助，请点击下方链接：

• 浏览技术支持中心
• 联系我们