
Newman 模型及其衍生模型构成了一套标准理论,该理论能够准确地预测锂离子电池在一系列工作条件下的设计性能。当使用 Newman 模型时,人们不必细致地描述电池电极的多孔结构,而只需要将常见的平均尺寸用作输入,即可将电极表征为均相的各向同性材料。然而,与详细的非均相几何模型相比,这种方法的准确度如何呢?让我们来一探究竟吧。
锂离子电池的不同建模方法
在锂离子电池建模领域,Newman 模型及其衍生模型占据着主导地位。由于此类模型基于多孔结构的均相化,所以使用者无需再详细描述多孔电极的三维几何结构。
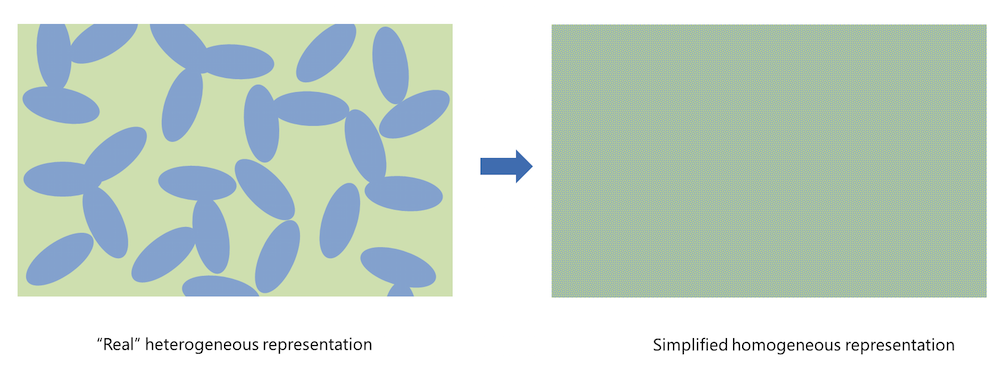
图1. 用均相化方式对真实的非均相多孔电极结构进行简化。
均相 Newman 模型
在模型中,均相化是指通过将真实的多孔结构被处理成固体粒子(上方左图中的蓝色部分)和孔隙电解质(绿色部分)组成的均匀混合溶液,从而将多孔结构近似表示为一个块厚板。采用均相化表征带来的结果之一是:孔隙电解质(离子导体)和电极中的导电颗粒(电子导体)被定义在了同一个几何域中。之后,我们使用孔隙率和迂曲度等变量来对有效电荷和质量传递属性进行描述,进而考察孔隙结构和颗粒对几何形状的显著影响。
均相多孔电极模型包含了在电极材料和孔隙内电解质之间电荷转移反应,此反应在实现电流传输的同时,也充当了电极和电解质区域电流的源和汇,并实现二者平衡,该反应类似溶液中两种化学物质之间均相反应。阴极的电荷转移反应是导体的平衡电流的源,同时也是用于维持孔隙电解质电流平衡的汇。采用上述的源和汇,根据法拉第定律和均相电荷转移反应的化学计量系数,可以实现模型中材料平衡的计算。
这些多孔电极模型对各类电化学电池中的多孔电极的建模和仿真帮助很大。但在描述锂离子电池多孔结构的详细设计时,这些模型是否有效呢?Tommy Zavalis(电池专家,COMSOL 前员工,现为 COMSOL 客户)和我在“神圣”的瑞典茶歇之间讨论了这个问题。结论是:只有将均相模型与非均相模型进行比较,才能知道这个问题的答案。为此,我们创建了一个非均相模型,以验证Newman 模型对理想的三维多孔电极仿真的有效性。
创建非均相模型
在非均相模型中,我们明确地将导电颗粒和孔隙间电解质描述为三维结构,并在空间建模时将二者处理成两个独立的域。
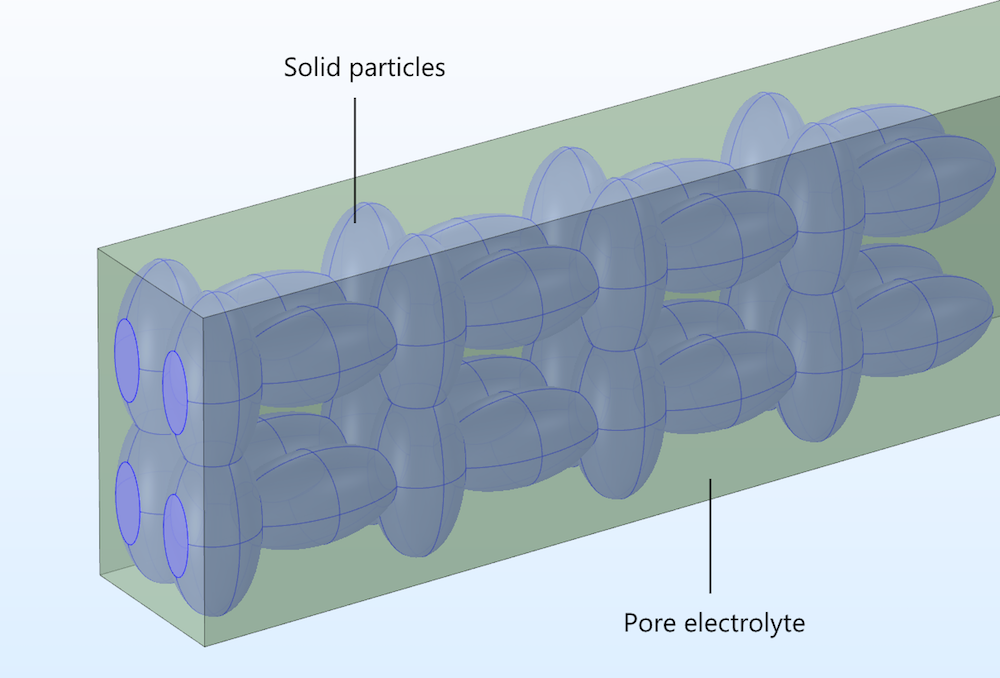
图 2. 理想多孔结构中的孔隙电解质域和粒子域。
离子迁移导致的电流守恒仅限于孔隙内电解质域,而导电颗粒的电流守恒仅限于固体电极区域。离子的质量传递仅定义在孔隙电解质域内,与此同时固体颗粒的表面存在一个边界,在该边界上,离子或溶液中的其它物质可以通过相间的电子转移进行反应。上述模型与均相模型形成了鲜明的对比,因为在均相模型中,材料平衡和反应均定义在整个均相电极的计算域中。
在模拟固体粒子表面形成的金属锂时,假设其仅在颗粒域中扩散,其中颗粒表面充当了外部边界。
评估 Newman 模型的准确性
现在,我们可以开始对比Newman 模型和非均相模型哪一个可以更加有效地用于描述精细的三维模型。建模实验十分简单:我们构建了一个包含理想三维多孔结构的理想电池单元,左右两侧的多孔结构相当于锂离子电池中的负极和正极。最终的几何模型如下图,其中流线的作用是说明自由电解质和孔隙内电解质中的电流流向。电极粒子由长轴方向各异的椭球组成,形成了导电阵列,电解质包含在粒子之间的空隙中。
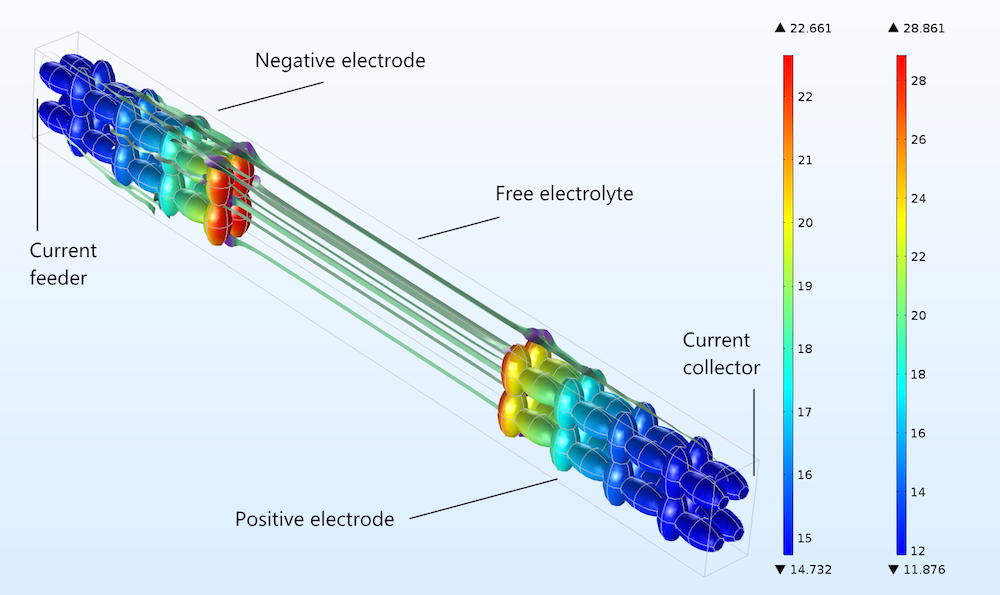
图3. 正极和负极中的电荷传递电流密度(A/m2)分布,分别对应右侧和左侧的几何结构与颜色图例。
上图显示了放电过程中固体粒子表面的电荷传递导致的电流密度的绝对值。在图中,正负电极面向集流体一侧比面向自由电解质(或分离膜)一侧的使用率更低。
我们可以通过旋转粒子的长轴方向,从而得到两种不同的沿电极长度方向的孔隙率分布,同时保持空隙-固体比率(孔隙率)总体不变。因为Newman 模型只使用总体的的平均孔隙率作为输入条件,当电极结构发生上述变化,其计算结果没有变化。
若将图 3中的电极旋转 180°,比如旋转下图中箭头所处的正电极,电流密度分布将随之变化,但是这种变化非常小(两张图的颜色图例对比说明了这一点)。即使使用电化学阻抗谱也很难检测出该电流分布的细微差异,对此我们将在下文进行探讨。
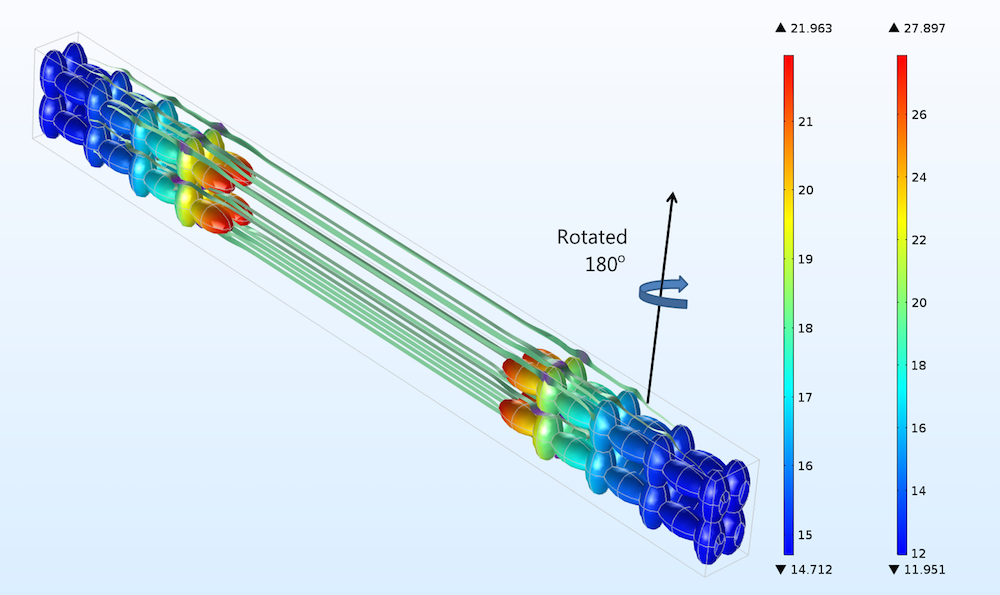
图 4. 当正极和负极均水平旋转 180°后,右正极和左负极的电流密度分布。建议与图 3 对比观察(上文只提到了正极的旋转)。
Tommy 和我喝着咖啡闲聊的时候曾做出这样的推测:可以使用类似于电化学阻抗谱(electrochemical impedance spectroscopy,简称 EIS)的方法,将不同时间尺度的电极的子过程进行分离,也许有能力捕捉到不同几何结构导致电流分布产生的差异。为此,我们分别采用非均相几何模型和均相Newman 模型对 EIS 实验进行模拟。
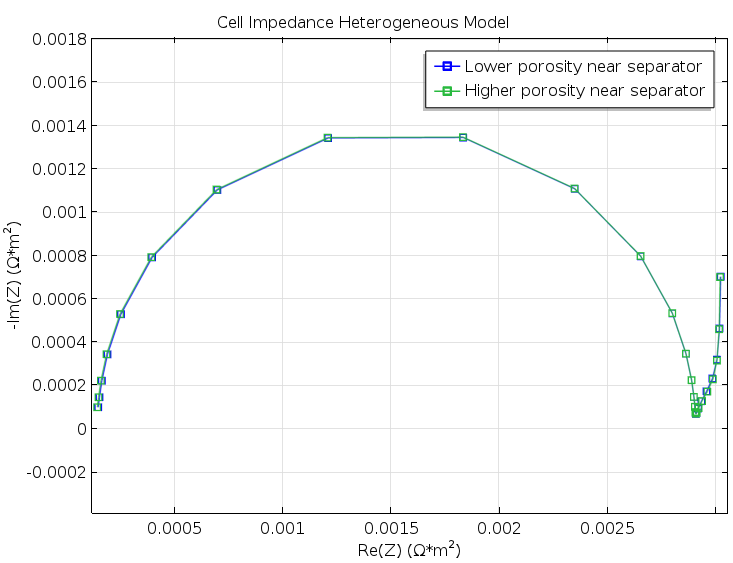
图5.图 3和图 4中两个模型几何的奈奎斯特图。二者的差异非常小,以至于无法通过真实实验进行检测。
实验结果喜忧参半。令人失望的是,如图 5所示,通过对两个几何结构进行模拟,我们得到的奈奎斯特图并没有显示图 3和图 4中的细微变化;令人惊喜的是,在没有任何参数拟合的情况下,Newman 模型与非均相模型表现出良好的一致性,具体请参照下图。这实在有点令人惊讶,因为我们的理想化结构在细节之处似乎过于粗糙,无法有效地进行均相化。举例来说,粒子尺寸比所模拟电池单元的宽度仅仅小一个数量级。
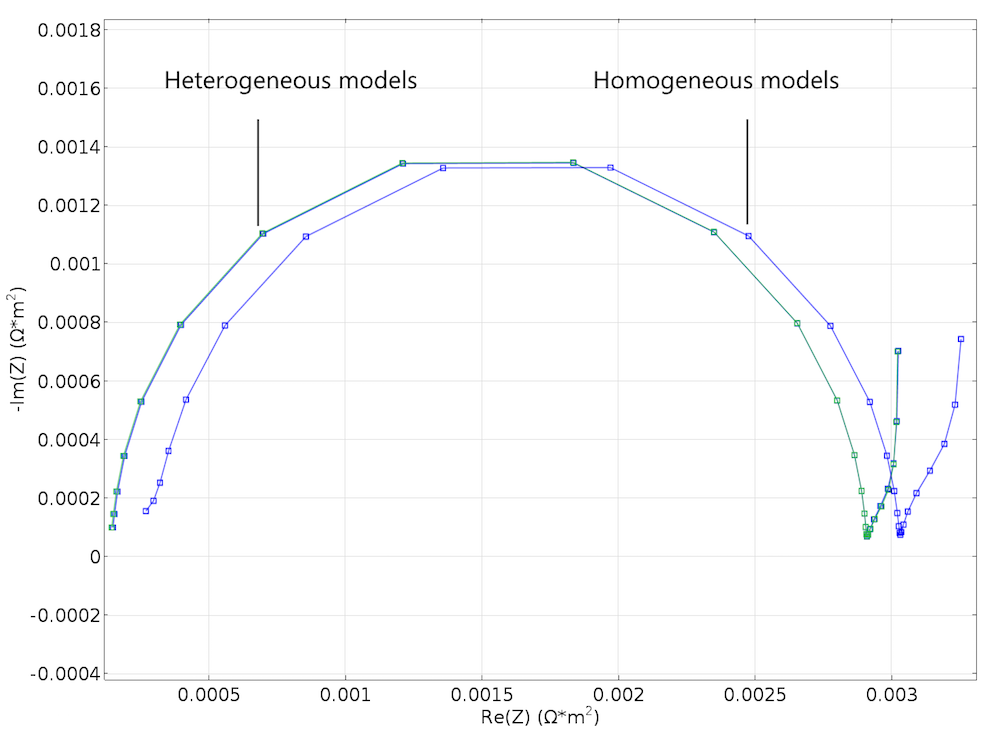
图6. 奈奎斯特图是利用 Newman 模型对 EIS 实验进行模拟而获得的。该图表与图 5中非均相模型的图表非常相似。
关于使用 Newman 模型和非均相模型模拟锂离子电池的总结
当然,最后还有一点!我们在上文中创建了一个简单的几何结构,并通过旋转电极使其结构发生变化,也许该变化太细微以至于无法给结果带来显著的影响。下一步自然是保持平均属性固定不变,尝试对详细几何模型进行更大幅度的更改。这样一来,我们就有可能捕捉到不同的非均相结构导致的结果差异,而这是均相的 Newman 模型无法实现的。
想自己动手尝试建模吗?点击下方链接,即可查看本文中模型的简介,同时还能下载用于生成仿真结果的 COMSOL Multiphysics 文件。您可以对模型进行任意的更改,并以此基础建自己的几何模型。
您可以阅读以下书籍获取更多信息:
- J. O’M. Bockris and A. K. N. Reddy,Modern Electrochemistry Volume 2, Springer-Verlag, 1970.
- J. Newman and K. E. Thomas-Alyea,Electrochemical Systems 3rdEdition, Wiley, 2004.



评论 (0)