热声发动机通过输入的热能产生声能。与往复式发动机和燃气涡轮机等常用发动机相比,热声发动机不含活动部件,因此结构非常简单。这篇博客,我们将介绍如何使用热黏性声学接口模拟热声发动机的工作原理。热黏性声学接口是 COMSOL Multiphysics®软件中的一个功能强大的接口,用于模拟流体线性化行为。
热声发动机的工作原理
150 多年前,Pieter Rijke 教授发现并报道了一个有趣的现象,可以被看作是热声学的开创性工作。他将金属丝纱布放入一个垂直放置的玻璃圆筒管中,然后用火从底部加热纱布。熄火后,他观察到圆筒在一段时间内持续发出声音(参考文献 1)。这个装置现在被称为Rijke管,因此有些人可能看到过它被作为解释共振现象的一个例子。然而,抛开共振不谈,声音是如何产生的呢?
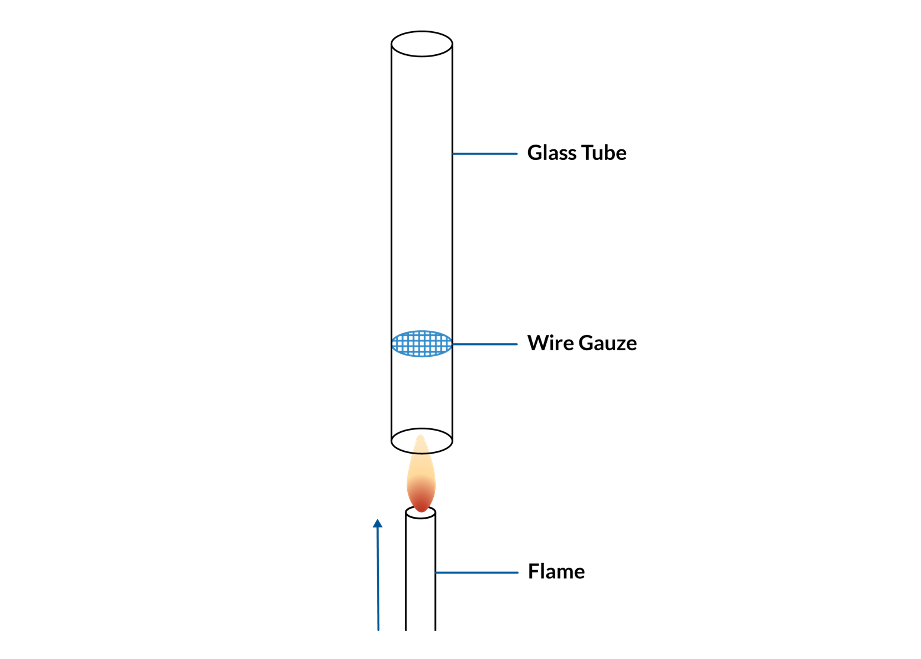
Rijke 管装置。
奥秘在于温度变化与管内流体运动之间的相互作用:加热的金属丝网引起空气自然对流,使空气在管道中稳定流动;金属丝网上方的空气温度要高于金属丝网下方的空气温度。在管内的半驻波声共振中,空气将在声周期的不同时间向两个方向流经金属丝网。当空气流过金属丝网时会被加热。由于金属丝网下方的空气比上方的空气更冷,因此当气流向上而不是向下流动时,会传递更多的热量。为了获得持续的声场,热量释放需要与压力场相位一致,这样当声压为正时,流体就会被加热。在驻波中,导致加热的速度场与压力场不同步。然而,由于金属丝网周围黏性边界层的影响,热量释放比速度场滞后。这种相位延迟导致热量释放与压力场部分同相,从而产生持续共振。如果将管横过来,对流停止,共振将不再持续。如果将管翻转过来,当声压为负时,热量传递将最大,因此声场将减弱而不是持续。
这是热能和声能之间能量转换的一个例子。事实上,整个装置展示了热声发动机的工作原理。
热声发动机有一个封闭的管状通道,声音可以在其中传播。通道内有一个热交换器,用于加热或冷却工作流体。热声发动机使用驻波或行波,而 Rijke 管仅使用驻波。由于压力和流体位移之间存在相位延迟,行波发动机有望实现比驻波发动机更好的性能。在这篇博客中,我们将主要介绍行波发动机的模型。
我们来思考一下使用行波的热声发动机的原理。要了解波是如何起作用的,请看下图中小块流体的运动。声波是纵波,因此如果高压行波从左侧传来,小块流体就会被推向右侧。同样,当来自左侧的低压波到达流体块时,它会被拉向左侧。
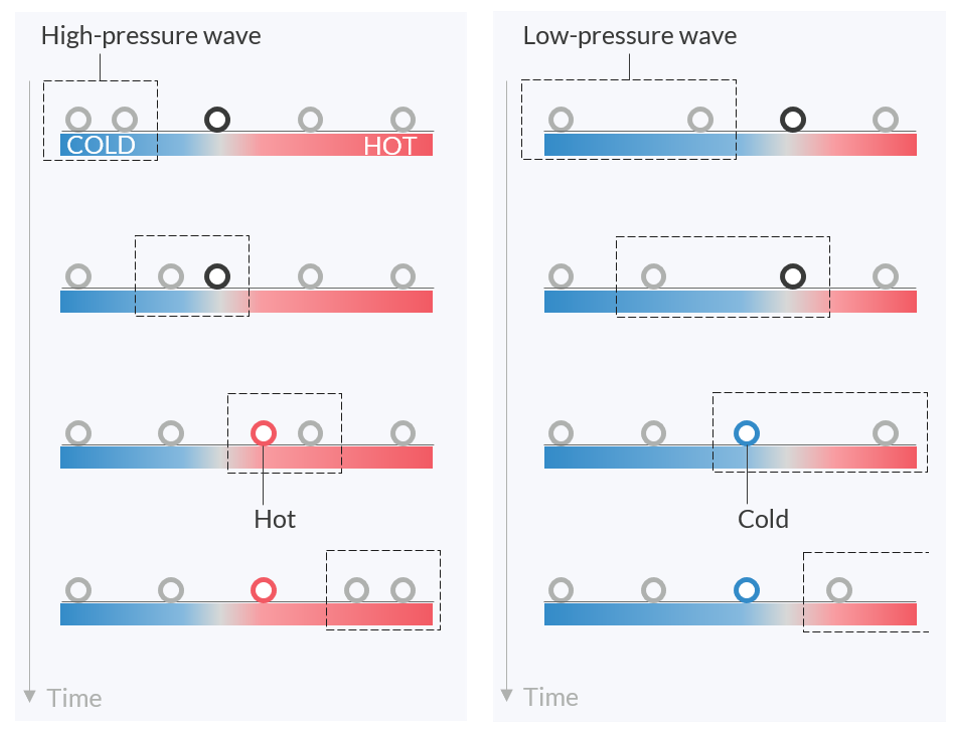
小块流体如何在来自左侧的行波下移动。用虚线框表示波的假想区域。在邻近板块有适当温度梯度的情况下,如果受到高压波的推动,流体块总是会移动到较热的区域,而如果受到低压波的牵引,流体块则会移动到较冷的区域。
假设沿波的行进路线在管中放置一块加热板。如果加热板的右端,而左端保持中等温度,那么加热板中就会出现温度梯度。当流体块向右移动时,温度梯度会加热块;当流体块向左移动时,温度梯度会吸收流体块的热量。由于流体块向右移动时压力最大,流体块的加热会将压力推至最大值。同样,流体块向左移动时吸收的热量也会降低最小气压。这些周期性的温度起伏使流体块的移动同步,最终增加了波的振幅。所有流体块像链条一样共同传递压力波,并通过热量交换为压力波增加能量。请注意,板中的温度梯度应与波的传播方向一致,否则波将会直接衰减。
如果你想知道是否存在一种与发动机循环相反的装置,答案是肯定的。这种系统被称为热声热泵或热声制冷机,它可以利用声波移动热量。工作原理很简单:当高压波到达块时,块被压缩,温度随之升高,块开始向右移动的同时向邻近物体散热。相反,在低压波的作用下,块会吸收热量并向左移动。
这里给出的解释仅供参考,并不包含热声发动机的所有细节。如果想了解有关热声发动机的更多详细信息,请参阅参考文献 2。
热声仿真中的线性方程
在创建新的仿真时,考虑使用哪些方程和哪个接口是合适的始终非常重要。就我们现在介绍的仿真示例而言,使用声学模块来模拟热声振荡似乎是合理的,因为这个现象与声波有关。由于这种现象在学术领域被称为热声学,因此热黏性声学接口似乎是一个不错的选择。让我们看一下这个接口的方程和功能,以验证我们的选择。
在时域分析中,热黏性声学接口使用以下方程:
式中,\rho,\bm{u},T, 和p分别表示密度、速度、温度和压力。下标{\cdot}_0表示该值属于背景平均流,而带有下标 的变量表示声学扰动。热黏性声学接口的控制方程是根据纳维-斯托克斯方程(流体运动的精确方程)推导出来的,并基于以下假设:模拟中可以忽略每一个二阶扰动项,并且平均背景流的速度为零 (\bm{u}_0=\bm{0})。
必须注意被忽略的非线性因素,以及线性化方程是否涵盖我们感兴趣的现象。在热声发动机中,流体与热交换器之间的热交换由扩散项\nabla \cdot (k\nabla T_{\rm t})表示,声振荡引起的热传递由线性化平流项\bm{u}_{\rm t}\cdot \nabla T_0表示。由高压平流项\bm{u}_{\rm t}\cdot \nabla T_0输送的冷流体在热交换器中被加热\nabla \cdot (k\nabla T_{\rm t}),能量通过第三个方程递增。这些项描述了系统中重要的热传递原理,因此线性方程非常适合模拟发动机。
另外还需要注意,没有表示时变温度场与振荡速度\bm{u}_{\rm t}\cdot\nabla T_t耦合的平流项。这种耦合表示法将显示振荡引起的瞬态温度场的传输。平流项对于热泵模拟非常重要,因为平衡时的温度梯度是由振荡决定的,而不是优先的。在这种情况下,我们可以使用非线性热黏性声学贡献功能,它允许模型在热黏性声学,瞬态接口中将非线性项考虑在内。模拟非线性可能代价高,因此非线性功能仅被添加在相关域中。
在 COMSOL Multiphysics®中进行热声仿真
到目前为止,我们已经介绍了热声发动机的基本工作原理和相关的模拟控制方程,下面我们就开始建立模型。您可以在COMSOL 案例库中访问文中示例的模型文件。如上一节所述,我们将使用热黏性声学接口来建立行波热声发动机模型。由于稳态背景温度场并不均匀,因此还要使用传热接口。整个研究可分为两个步骤:背景温度场的稳态步骤和声场的瞬态步骤,而不是同时使用两个接口。只需在热黏性声学模型节点中将传热接口的解设置为平衡温度,就可以实现耦合。
至于热黏性声学接口的边界条件,我们应将热交换器壁设置为等温 (T_{\rm t} = 0)。这种条件会在压力较高时加热流体温度(由于来自较冷区域的平流,T_{\rm t}小于零),并在压力较低时冷却流体(T_{\rm t}大于零)。
示例 1:简单环
首先,我们将模拟一个由简单环组成的发动机。它的右侧通道中有一个热交换器,整个通道形成一个闭合回路。稳态温度如下图所示。热交换器下部区域的温度梯度非常醒目,但我们关注的是热交换器小间隙中的温度梯度。
简单环形发动机的平衡温度(左:整个系统;右:热交换器特写)。热交换器中狭窄通道的底部端在 493 K 的温度下被加热。
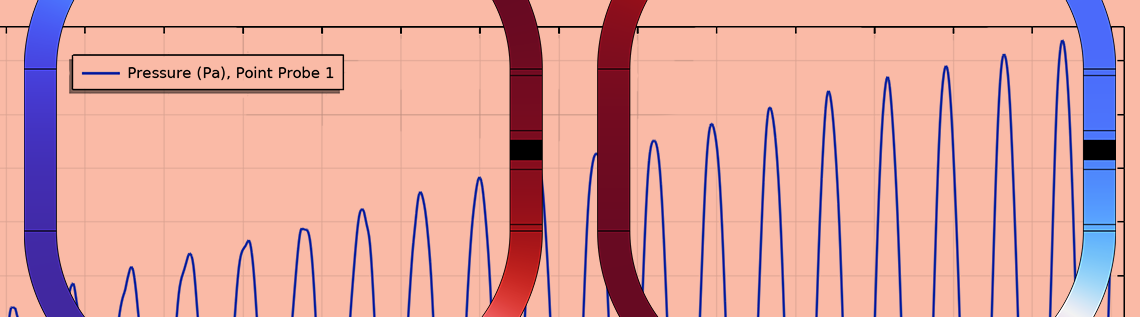
在瞬态研究步骤中,驻波被作为压力的初始条件,以便触发环路内部的振荡。随着模拟的继续,振幅不断增大,这可通过点探针功能获取(如下图所示)。很明显,振荡不断增强,意味着热能已转化为声能。

设置点探针功能是为了追踪发动机内的压力。压力数据取自热交换器中的一个点,该点靠近作为初始压力分布的驻波的压力节点。
那么,发动机内的压力是怎样的呢?下面三幅图分别显示了 t = 0.281 s、0.285 s 和 0.289 s 时的压力分布。t = 0 s 时为驻波,但经过一小段时间后,压力分布开始沿顺时针方向旋转。波的传播方向与热交换器中的温度梯度相同,初始驻波的逆时针分量由于缺乏能量供应而减弱。有趣的是,逆时针方向的波的激发可以通过在模拟过程中翻转温度梯度的方向来模拟。在模型文件中,稳态研究步骤在 t = 0.3 s 时再次计算反转后的温度曲线,瞬态研究反映了自那时起平衡温度的变化。顺时针方向的波一直保持到大约 t = 0.6 s。随后,发动机中出现了类似驻波的分布,波最终沿逆时针方向传播。

压力分布记录(左:t = 0.281 s;中:t = 0.285 s;右:t = 0.289 s)。由于前面讨论的热声效应,高压区和低压区均沿顺时针方向移动。
示例 2:带接头的环
除简单环外,我们再来看看另一种配置。下图显示了下一个具有复杂几何结构的模型示例。该几何结构模仿了参考文献 3 中的实验装置。该模型是二维的并经过简化,与参考文献中讨论的热交换器的水力直径相同。右下角的分支管道(称为接头)是为将来提取声能而添加的。与示例 1 一样,该环路用在发动机中将热能转换为声能,但是在这个示例中,部分能量可以在接头处提取。
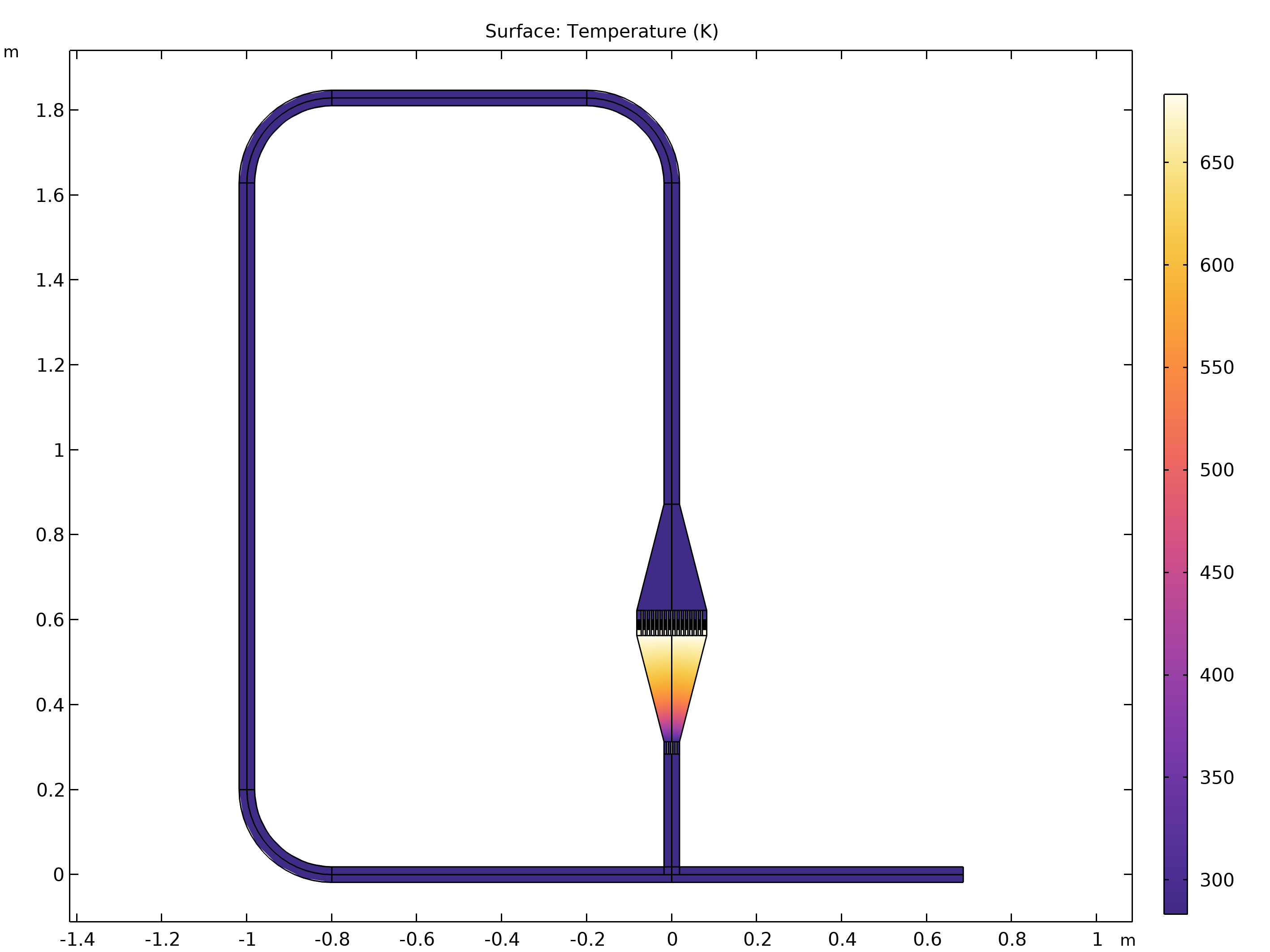
带接头的模型中的平衡温度。该几何结构模仿了参考文献 3 中的实验装置。
发动机内的瞬时压力分布如下图所示。在弧长等于 3.6 m时,压力急剧下降,这是由热交换器小间隙中的黏性阻力引起的。值得注意的是,压力的振幅与位置密切相关。这是由于模型的复杂性造成的,例如发动机中持续存在的黏性阻力和驻波分量。图中还绘制了每个位置上绝对压力的时间最大值,标记为max(|p|)。请注意,尽管振幅看起来有点大,但该模拟假设没有湍流,任何扰动都是线性的。在对空间最大值进行无量纲化处理后,近似振幅max(|p|) 的分布与参考文献 3 中的实验和分析数据非常吻合。
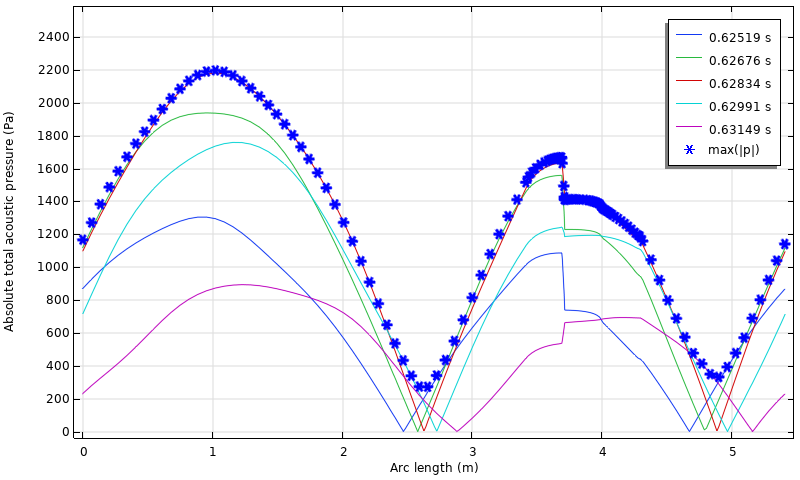
沿环的瞬时压力分布以及由状态变量计算的近似振幅max(|p|)。
查看其他示例
自 Rijke 教授演示了热声现象以来,人们对热声学的认识有了显著提高,目前正在积极研究其在能源设备中的应用。在这篇博客中,我们介绍了如何使用热黏性声学接口对热声发动机进行模拟,并对发动机的有趣特性进行了可视化展示。
COMSOL 案例库包含许多跨物理学科的模型。下面是与热声学有关的两个模型:
- 热声发动机简化模型, 这是一个驻波热声发动机模型。有多个模型文件,可对使用热黏性声学,瞬态接口的线性扰动方法和非等温流动多物理场接口的完全非线性方法建立同一模型进行比较。后一种方法在求解纳维-斯托克斯方程时考虑了非线性因素,但代价是计算时间有所增加。
- 热声发动机和热泵, 这是一个驻波热泵模型。与热声发动机不同,热声热泵的仿真需要计算非线性平流项\bm{u_t}\cdot\nabla T_{\rm t},因为温度会因热传导效应而不断降低。在模型中,非线性热黏性声学贡献节点被添加到热黏性声学接口中,以考虑非线性因素。模型还使用了热黏性声学-热扰动边界耦合,这是 6.2 版本中的一项新功能。该耦合用于模拟振荡流体与通道中的固体板之间的热交换,因为固体温度会随着热量的泵送而不断降低。
参考文献
- P.L. Rijke, “LXXI. Notice of a new method of causing a vibration of the air contained in a tube open at both ends,”The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 17, no. 116, 419–422, 1859;https://doi.org/10.1080/14786445908642701
- G.W. Swift,Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, Springer, 2017;https://doi.org/10.1007/978-3-319-66933-5
- M. McGaughy et al., “A Traveling Wave Thermoacoustic Engine—Design and Test,”Letters Dyn. Sys. Control, vol. 1, no. 3, July 2021;https://doi.org/10.1115/1.4049528



评论 (0)