
在声泳力系列博客中,我们讨论了声辐射力的性质,以及在 COMSOL Multiphysics® 软件中计算这种力的不同方法。今天,我们将向您介绍一种与此相关的现象,即声学轨迹角动量,并演示如何对它进行仿真。
音速起子
自 1963 年首次在电视上播放以来,《神秘博士》(Doctor Who® )电视节目一直关注着“神秘博士”的时空旅行。当登上他的时空旅行宇宙飞船(一个叫做 TARDIS® 控制台的蓝色英国警察电话亭)时,就像粉丝们所熟知的,这位博士会经常带上他的新的同伴来分享他的冒险经历,以及一个非常有用的工具:音速起子。
顾名思义,音速起子是通过声波对远处的物体产生力来使用的。对于神秘博士来说,这个工具在各种情况下都非常有用,无论是开锁还是解除武器武装。音速起子的功能可能是虚构的,但它背后的物理原理却是基于一个真实的理论。

《神秘博士》电视节目中的音速起子。图片来源:Sonicdrewdriver,CC BY-SA 3.0, 通过Wikimedia Commons共享。
就像我们在之前的博客中强调的那样,声辐射力是一种由粒子对入射声波的非线性响应所产生的现象。波携带的一小部分线性动量被粒子不可逆地吸收,从而产生净力。与线性动量一样,由于非线性效应,声学轨迹角动量(OAM)被实体对象不可逆地吸收,从而产生净扭矩。在一个固体圆盘和微粒施加扭矩的观察实验中,这一现象已经得到了证实。
在这篇博客中,我们将在 COMSOL Multiphysics 的帮助下分析声学轨迹角动量。
了解声学轨迹角动量
声波仿真是对波动方程求解的结果。这些方程的一些解允许具有与声涡相关的轨迹角动量的场。这种场可以在具有圆柱对称性的设备中自然实现,并通过相对于对称轴的相位奇点来识别,并使用相位\text{e}^{im\phi}的形式来表示这个奇点。在这种情况下,\phi是方位角,m是一个整数(称为拓扑电荷),相位r= 0轴上的复值函数。
考虑一种可以产生声涡的实用设备,例如圆形超声波阵列。该设备(如下所示)由径向极化 PZT 探头的圆形阵列组成,其中每个阵列元件都可以独立通电。换能器环内部的空间可以充满任何液体(例如水)。用于激励阵列的发生器控制着每个元件电压的相位和幅度。因此,对流体体积内部产生的声场的控制水平很高。
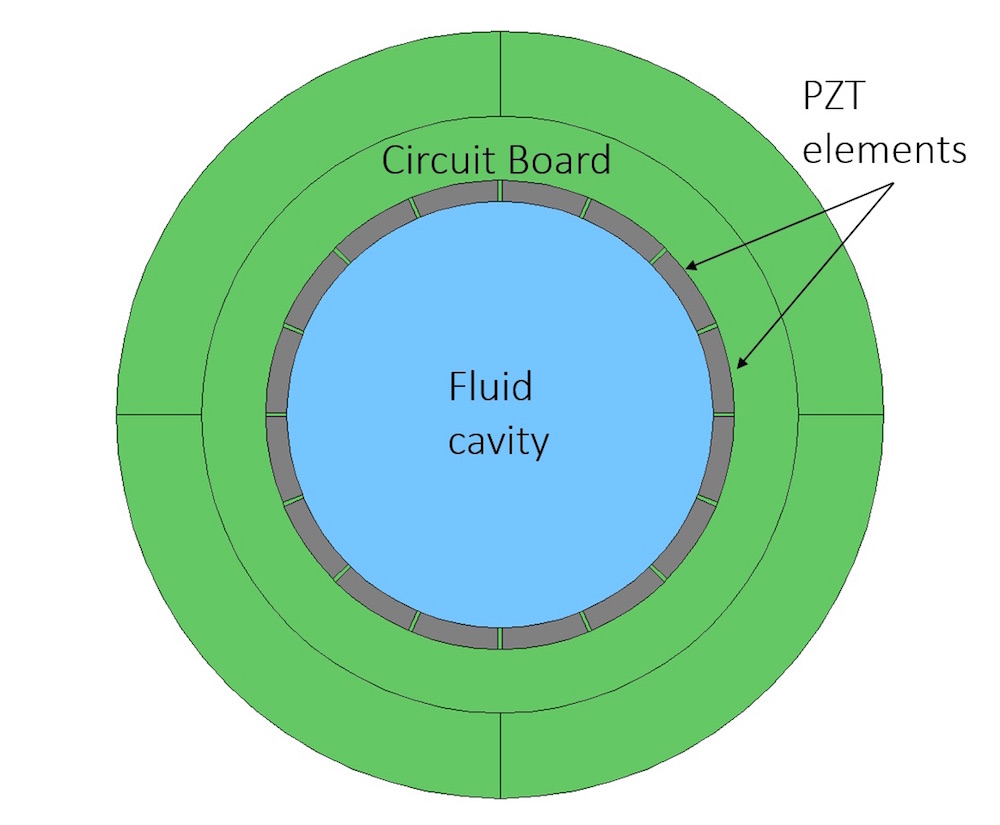
16单元圆形超声阵列装置示意图。
贝塞尔场模是这种阵列中可以实现的最简单的场分布。这些模对应于驻波场,其振幅的径向分布由第一类贝塞尔函数J_m(kr)定义,对应波长\lambda的波数是k=2\pi/\lambda。同时,场的角依赖于相应阶数m的指数,这样才能使流体中的压力分布为p(r,\phi) \propto J_m(kr)\text{e}^{im\phi}。
在流体体积中心附近实现了纯贝塞尔场分布。场分布由于更高阶的模态而变得扭曲,这是由于离阵列中心有一定距离的单元数量有限引起的混叠效应的结果。在这个解中,指数相位项决定了声场内的轨迹角动量。为了激发mth阶声场,换能器通过阵列的相邻元件之间的相位差2\pi m/N(N是元件的数量)通电。以下动画描绘了旋转声场。
在 16 单元圆形超声阵列装置中产生了m=1贝塞尔模。内部半径为 0.5cm,对应于 1.23mm 波长的频率为 1.2 MHz。
是曳力还是轨迹角动量传递?
当粒子被引入旋转的贝塞尔场时,将对它施加两个声学力和一个由声学轨迹角动量传递产生的扭矩。作用在径向方向上的第一个力是直接的声辐射力,它将粒子拉到贝塞尔场的节点。第二个力作用在方位方向上,是声辐射力的间接贡献。由声流效应引起的流动循环产生了曳力。在之前的一篇博客中,我们解释了如何在 COMSOL Multiphysics 中对这种效应进行建模。
这两种力的结合使粒子以螺旋运动移动。螺旋运动在流体体积的中心部分向轴线收敛。
流体体积中央部分的粒子轨迹。粒子被拉向贝塞尔函数的节点,声流中的黏性曳力产生旋转。
上述动画中的粒子轨迹是使用 COMSOL Multiphysics 的流体流动颗粒追踪接口中的曳力和声泳辐射力节点计算的。用于计算这些力的输入场是从求解声场分布(来自热声学接口)和流体流场分布(来自层流接口,体积力来自声场)中获得的。虽然曳力可以解释粒子偏离轴的旋转,但粒子的径向速度在接近轴时减小,这使得中心粒子簇的径向速度为零。这是意料之中的,因为流体不能支持轴上的奇点。因此,径向速度在轴上必须接近零。
这样的结果与实验观察相矛盾,在实验观察中,中心的粒子团被证明以相当大的角速度旋转。这表明,虽然在制作这个动画时考虑的两种力可以解释远离轴的孤立粒子的行为,但它们并不足以解释轴上的粒子团的旋转。这些结果只适用于计算孤立的小颗粒上的力。
为了解释观察到的旋转,我们必须考虑两个来自中心的粒子团大小的额外效应。相较于小颗粒,聚集的粒子团或颗粒将吸收更大的声学轨迹角动量和黏性曳力。尽管如此,这些力基本来源是声场,因此这两种效应都可以被看作声场的声学轨迹角动量转移到粒子团的不同机制。
在许多由不同的设备产生声涡的实验中,已经观察到了声学轨迹角动量向粒子的转移。这篇博客中的示例只是众多例子中的一种。那么,这到底是不是用来武装神秘博士的声波起子技术,还有待未来(或过去)的观察。
声泳力学系列的其他博客
延伸阅读
- 博客:声辐射力的热黏性分析。
- Z. Hong, J. Zhang, and B. W. Drinkwater, “Observation of Orbital Angular Momentum Transfer from Bessel-Shaped Acoustic Vortices to Diphasic Liquid-Microparticle Mixtures“, Phys. Rev. Lett. 114, 214301
- A. Anhäuser, R. Wunenburger, and E. Brasselet, “Acoustic Rotational Manipulation Using Orbital Angular Momentum Transfer“, Phys. Rev. Lett. 109, 034301
- F. G. Mitri, T. P. Lobo, and G. T. Silva, “Axial acoustic radiation torque of a Bessel vortex beam on spherical shells“, Phys. Rev. E 84, 065601(R)
- A. Grinenko, P. D. Wilcox, C. R. P. Courtney, and B. W. Drinkwater, “Proof of principle study of ultrasonic particle manipulation by a circular array device“, Proc. R. Soc. A doi:10.1098/rspa.2012.0232
神秘博士和 TARDIS 是英国广播公司 (BBC) 的注册商标。BBC 与 COMSOL 没有关联、连接或关联,也没有制作、赞助或批准 COMSOL 的软件或本博客内容。



评论 (0)