Menu
COMSOL 博客

使用 COMSOL Multiphysics®模拟多孔介质的声学特性

Author Image

作者Kirill Horoshenkov

Guest
2021年 1月 14日

今天的特邀博主 Kirill Horoshenkov（FREng）是来自英国谢菲尔德大学（the University of Sheffield）的声学教授，他讨论了如何使用 COMSOL Multiphysics®软件和声学模块模拟多孔介质的声学特性。

对于多孔介质的声学特性，我们感兴趣的方面是它对入射声波具有极强的吸收和修改能力，其中入射声波与填充材料孔隙的流体会发生相互作用。黏性摩擦、惯性和热耗散效应是产生刚性结构多孔介质声学特性的主要原因。这些效应受材料的孔隙率和其他孔隙结构参数影响。对于大多数实际工程问题而言，尽管我们并不直接关注多孔材料的声学特性，但研究声学特性、孔隙率和结构形态之间的关系却非常有意义。

在与能量存储相关的应用中，测量影响多孔隔板的电解质吸收及导电能力的陶瓷隔板的孔隙率和曲折率非常重要；在与过滤操作相关的应用中，定期测量与上述相似的特性可以确定在有流体流动的情况下膜的渗透性；在制药应用中，通常需要测量平均粒度和压实度，粒度分布以及颗粒混合物吸收的水分量。在化学和化学工程应用中，重要的是要了解材料的内部孔隙表面积，用于通过输送催化剂控制化学反应并将有毒物质转化为化学惰性键。在噪声控制应用中，我们关注的是评估多孔层吸收声音的能力。

6 参数 Johnson–Champoux–Allard–Lafarge 模型

COMSOL Multiphysics 软件包含一系列可以预测多孔介质声学特性的模型。在以往的应用中，声学模块的多孔介质声学功能（图1）中所包含的 Johnson-Champoux-Allard-Lafarge（JCAL）模型一直用于此目的，其结果被广泛参考（截至 2020 年 11 月 15 日，已有超过 2000 个 Scopus 文摘和引文数据库引用）。

JCAL 模型最初于 1991 年被提出（参考文献1）。它需要 6 个非声学参数来预测材料孔隙中流体复杂的、随频率变化的动态密度：

(1)

\rho(\omega)=\frac{\rho_f \alpha_\infty}{\epsilon_p} \left[ 1+\frac{\sigma \epsilon_p}{i \alpha_\infty \rho_f \omega} \left( 1+\frac{4i \alpha ^{2}_\infty \mu \rho_f \omega}{\sigma^2 \Lambda^2 \epsilon^{2}_{p}}\right)^{1/2} \right]

以及动态可压缩性

(2)

C(\omega) = \frac{\epsilon_p}{\gamma P_0} \left[\gamma – \frac{\gamma-1}{1-\frac{i \sigma’ \epsilon_p}{\rho_f \alpha_\infty N_\textrm{Pr} \omega} \left(1+\frac{4i \alpha^{2}_{\infty}\mu \rho_f N_\textrm{Pr}\omega}{(\sigma’ \Lambda’ \epsilon_p)^2}\right)^{1/2}} \right]

图1 多孔介质声学接口的设置窗口的屏幕截图，显示了 JCAL 模型的 6 个原始参数的设置。

在COMSOL文档和由Matelys运营的声学多孔介质设计（Acoustical Porous Material Recipes，APMR）网站中，对这些方程的物理含义进行了全面的解释。在上述公式中，影响多孔介质声学特性的关键非声学参数为：

  1. 孔隙率，\epsilon_p
  2. 黏性流阻，\sigma
  3. 热流阻，\sigma’
  4. 黏性特征长度，\Lambda
  5. 热特性长度\Lambda’
  6. 曲折因子，\alpha_\infty

式中，\Lambda是孔尺度的度量，在该尺度上，黏性和惯性效应特别明显。\Lambda’也是孔尺度的度量，其中的热耗散效果特别明显。\alpha_\infty用于度量孔的扭曲度以及声波在多孔层中传播时的路径复杂度。通常，黏性和热流阻被其对应的静态渗透率所代替，即\kappa_0=\mu / \sigma和\kappa_0’=\mu / \sigma’。上式中的其他参数是标准的且均已知：

  1. 流体的平衡密度，\rho_f
  2. i = \sqrt{-1}
  3. 声音的角频率，\omega
  4. 流体的动态黏度，\mu
  5. 普朗特数，N_\textrm{Pr}

多孔介质的主要声学特性是特征阻抗和波数，分别由下式定义

(3)

z_b(\omega) = \sqrt{\rho(\omega) / C(\omega)} \qquad \textrm{和} \qquad k_b(\omega)=\omega \sqrt{\rho(\omega) C(\omega)}

编者注：COMSOL 中使用的表示法略有不同。详请参阅《声学模块用户指南》中有关多孔介质声学模型简介部分的内容。

直接测量特征阻抗和波数并不常见，尽管确实存在用于测量这些量的实验方法，例如 Doutres 等人提出的三麦克风阻抗管方法（参考资料2）。但是，目前尚无一致的标准方法来衡量z_b和k_b。国际上最流行的用于测量多孔介质声学特性的 ISO 标准实验方法是使用两麦克风声阻抗管法（参考文献3）。根据该标准，复反射系数可以表示为：

(4)

r(\omega)=\frac{z_s(\omega)-1}{z_s(\omega)+1}

归一化表面阻抗可表示为：

(5)

z_s(\omega)=z_b(\omega)\coth(ik_b(\omega)h)/(\rho_f c_0)

该实验是对硬背壁反射表面的厚度为h的声学材料在一个频率范围内进行测量，其频率范围受阻抗管的直径和两个麦克风之间的间距限制（详请参阅参考文献3中的 4.2 节）。

式中，c_0是流体中声速。通常，通过参数反演（参考文献4）或其他拟合程序将模型拟合到测得的表面阻抗或反射系数数据中。

编者注：阻抗管教程模型详细介绍了如何通过数据生成估算参数。

结果表明，JCAL 模型通过参数可以很好的拟合具有任意孔隙几何形状和孔径分布的各种多孔介质，例如，纤维材料（参考文献5中的第 IV 部分）、粒状介质（参考文献6）和泡沫塑料（参考文献7中的第 V 部分）。问题是如何在不拟合的情况下进行测量，并准确设置 JCAL 模型所需的 6 个参数的值来预测可能无法很好的表征特定材料的声学特性。尽管使用非声学方法确定孔隙率和黏性流体的阻抗相对简单，但测量黏滞特征长度\wedge，热特征长度\wedge’和热渗透率k_0′也绝非易事，需要高度复杂的实验室设置。同样，测量曲折率\alpha_\infty也不容易。因此，很少测量这 4 个参数，通常会进行猜测或从拟合到的数据逆推。

从 6 个参数到 3 个参数的 JCAL 模型

最近，Horoshenkov 等人（参考文献8–9）证明在 JCAL 模型中根本不需要使用 3 个以上的参数。作者通过理论（参考文献8）和实验（参考文献9）验证表明，仅通过以下 3 个可直接测量的非声学参数，就可以预测具有一定孔径分布的多孔介质的表面声阻抗：

  1. 孔隙率，\epsilon_p
  2. 平均孔径，\bar{s}
  3. 孔径标准偏差，\sigma_s

结果表明：

\Lambda = \bar{s}e^{-5/2(\sigma_s \text{log} 2)^2}
\Lambda’=\bar{s}e^{3/2(\sigma_s \text{log}2)^2}
\kappa_0=\frac{\bar{s}^2\epsilon_p}{8 \alpha_\infty}e^{-6(\sigma_s\text{log}2)^2},\quad \sigma=\mu/\kappa_0
\kappa_0’=\frac{\bar{s}^2\epsilon_p}{8 \alpha_\infty}e^{6(\sigma_s\text{log}2)^2}, \quad \sigma’=\mu/\kappa_0′

和

\alpha_\infty=e^{4(\sigma_s\text{log}2)^2}.

这种方法有效地将预测多孔介质声学特性所需的参数数量减了一半。文献中建立的新模型非常适用于使用声学数据测量和求逆多孔介质的关键非声学特性，这些介质可用于各种应用且并不一定是声学应用。作者还提出了一种新的理论模型（Padé 近似），用于预测材料孔隙中流体的体积动态密度和可压缩性（参考文献8），COMSOL Multiphysics 软件自 5.6 版本起就包含了此模型。

在 COMSOL Multiphysics®中选择 3 参数模型

图2 的屏幕截图显示了如何从 COMSOL Multiphysics 5.6 版本以上的压力声学，频域接口的多孔介质声学功能中选择新的 3 参数模型。选择该模型需要了解材料的孔隙率\epsilon_p（无量纲），平均孔径\bar{s}[m] 和孔径的标准偏差\sigma_s[\phi-units]（参考文献8）。我们可以在多孔介质声学设置的底部选择这些参数的适当值，如图2所示。

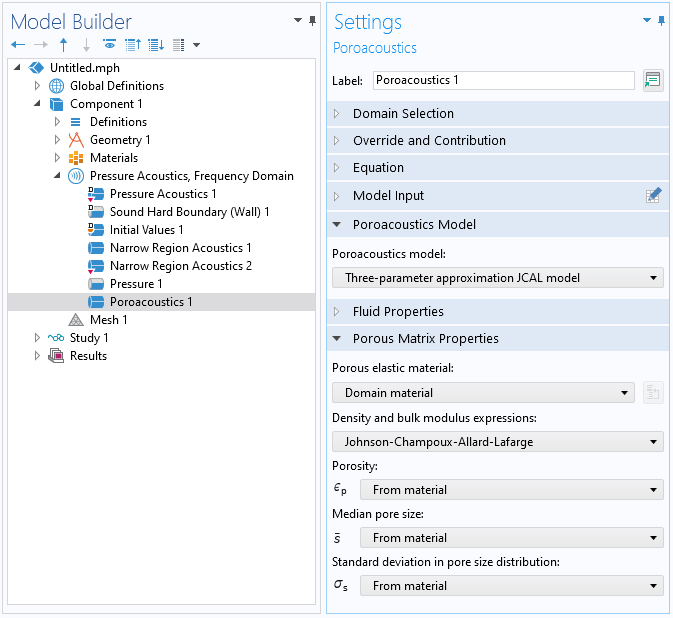
The Poroacoustics interface settings with the Poroacoustics Model and Porous Matrix Properties sections expanded.
图2 多孔介质声学接口的屏幕截图，显示了新的 3 参数模型的设置。

我们可以在多孔介质声学特征中选择3参数近似JCAL模型，来使用此 3 参数模型。多孔介质声学特征将使用原始 JCAL 方程计算动态密度和压缩系数（方程1-2），或使用参考文献8中提出新方程来计算这些量。我们可以通过设置密度和体积模量表达式来进行选择，也可以选择 Johnson-Champoux-Allard-Lafarge 模型使用原始 JCAL 方程。否则，请选择参考文献8中建议的 Padé 近似值。除了 Padé 近似更匹配的等效流体在具有圆柱孔的多孔介质（参考文献8）中的真实低频特性之外，动态密度和压缩系数的选择对预测结果没有太大影响。

对于一个硬背壁反射厚度为 16.5 mm 的三聚氰胺泡沫，图3显示了测得的归一化表面阻抗谱z_s(\omega)。此图还显示了使用原始 JCAL 模型（虚线）和参考文献8（实线）中提出的模型，在相同参数设置\epsilon_p=0.998，\bar{s}=115\mum 和\sigma_s=0.234\phi-units 下进行的预测。由图中可以看出，两组线几乎没有区别，精确度在 4％ 以内，比由阻抗管实验所得的 5％ 重现性结果更好。

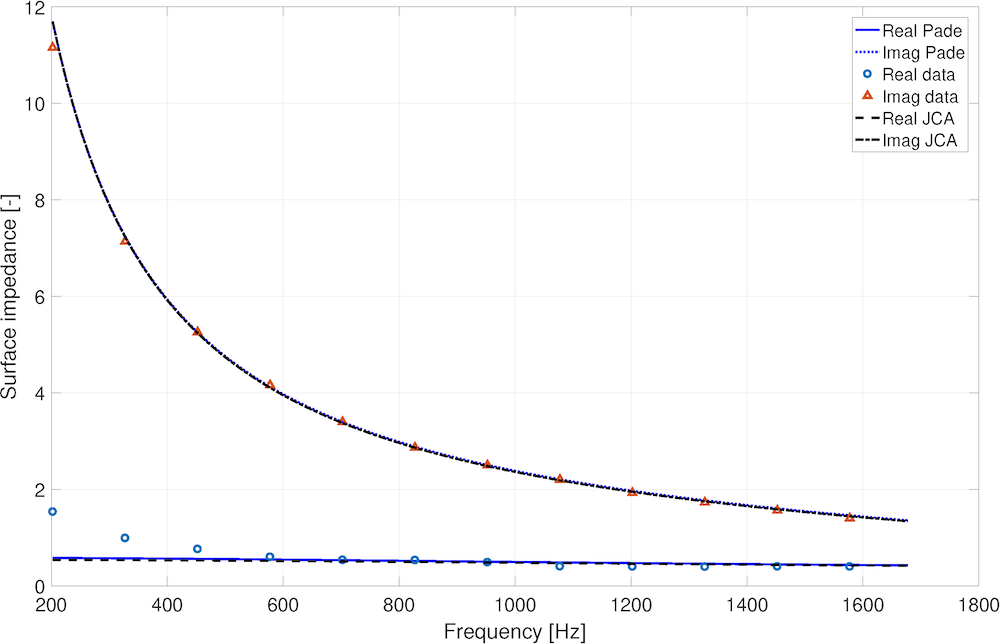
A graph plotting the normalized measured and predicted complex surface impedance spectra for a sample of foam.
图3 对硬背壁反射的厚度为 16.5 mm 的三聚氰胺泡沫的归一化复表面阻抗谱的测量值和预测值进行比较。

3 参数模拟的应用示例

下面，我们来看一个模型应用示例。以一个直径为 25mm 的波导为例，其中装有一个用于增加阻尼的具有多孔内层的亥姆霍兹共振器，内层为厚度 21.5 毫米的毛毡层，参数如下：\epsilon_p=0.998,\bar{s}=147\mum, 和\sigma_s=0.325\phi-unit。该问题描述如图4 所示。

第一个问题：包含共振器的情况下，声音传播的吸收系数、反射系数和传输系数分别是多少？另一个问题：使用基于 JCAL 和 Padé 近似的 COMSOL 模型模拟，是否可以得出相似的结果来预测毛毡的声学特性？图4 给出了该模型模拟的结果。模拟结果表明，对于这个特定问题，两个模型的预测结果几乎一致。该模型中使用的毛毡参数具有很好的物理意义，因为它们已经通过了非声学实验验证（参考文献9）。

A waveguide model with a Helmholtz resonator branch in the context of the COMSOL Multiphysics Model Builder UI.
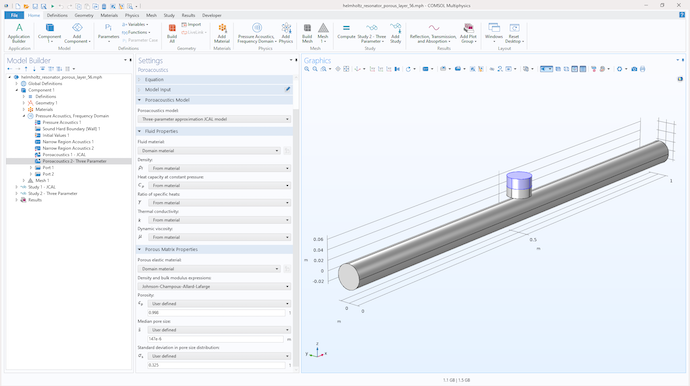
图4：在 COMSOL Multiphysics 中模拟的含亥姆霍兹共振器的波导模型。

A graph comparing the predicted reflection, transmission, and absorption coefficient spectra through the waveguide model with the Helmholtz resonator branch.
图5 通过含亥姆霍兹共振器的波导预测的反射、透射和吸收系数谱的比较。

动手尝试

单击下面的按钮，尝试模拟文中介绍的含多孔层的亥姆霍兹谐振器。

获取模型

参考文献

  1. Champoux, Y. and Allard, J.-F., “Dynamic tortuosity and bulk modulus in air-saturated porous media”,Appl. Phys., vol. 70, no. 4, pp. 1975–1979, 1991.https://doi.org/10.1063/1.349482
  2. Doutres, O., Salissou, Y., Atalla, N., Panneton, R. “Evaluation of the acoustic and non-acoustic properties of sound absorbing materials using a three microphone impedance tube”,Acoust., vol. 71, no. 6, pp. 506–509, 2010.http://dx.doi.org/10.1016/j.apacoust.2010.01.007
  3. ISO 10534-2:1998, “Determination of sound absorption coefficient and impedance in impedance tubes, Part 2: Transfer-function method”,International Organization for Standardization, Geneva, Switzerland, 1998.https://www.iso.org/standard/22851.html
  4. Horoshenkov, K. V., “A Review of acoustical methods for porous material characterisation”,J. Acoust. Vib., vol. 22, vol. 1, pp. 92–103, 2017.https://doi.org/10.20855/ijav.2017.22.1455
  5. Allard, J.-F. and Champoux, Y., “New empirical equations for sound propagation in rigid frame fibrous materials”,Acoust. Soc. Am., vol. 91, no. 6, pp. 3346–3353, 1992.https://doi.org/10.1121/1.402824
  6. Allard, J.-F., Henry, M. Tizianel, J., Kelders L. and Lauriks, W., “Sound propagation in air-saturated random packings of beads”,Acoust. Soc. Am., vol. 104, no. 4, pp. 2004–2007, 1998.https://doi.org/10.1121/1.423766
  7. Perrot, C., Chevillotte, F., Hoang, M. T., Bonnet, G. BÃl’cot, F.-X., Gautron, L. and Duval, A., “Microstructure, transport, and acoustic properties of open-cell foam samples: Experiments and three-dimensional numerical simulations”,Appl. Phys., vol. 111, no. 014911, 2012.https://doi.org/10.1063/1.3673523
  8. Horoshenkov, K. V., Groby, J.-P., and Dazel, O., “Asymptotic limits of some models for sound propagation in porous media and the assignment of the pore characteristic lengths”,Acoust. Soc. Am., vol. 139, no. 5, pp. 2463–2474, 2016.https://doi.org/10.1121/1.4947540
  9. Horoshenkov, K. V., Hurrell, A. and Groby, J.-P., “A three-parameter analytical model for the acoustical properties of porous media”, vol. 145, no. 4, pp. 2512–25178, 2019.https://doi.org/10.1121/1.5098778

致谢

文中模型的几何形状和参数由英国谢菲尔德大学机械工程系的 Alexander J. Dell 提供。

关于作者

Kirill Horoshenkov（FREng）是英国谢菲尔德大学（University of Sheffield，UK）机械工程系的声学教授。他于 1989 年毕业于俄罗斯莫斯科无线电工程与自动化大学（Moscow University for Radioengineering and Automatics, Russia），并获得了电声与超声工程学硕士学位。1997 年，他获得了英国布拉德福德大学（University of Bradford，UK）的声学博士学位。他的研究包括室外声音传播、多孔介质的声学以及机器人的声学感应。由他带领EPSRC Programme Grant Pipebots和EPSRC UKAcoustics Network 超过了 1000 名成员。他发表了超过 90 多篇经评审的期刊论文和相似数量的会议论文，拥有 10 项专利或专利申请（作者或合著者）。三项以他的名字或由他直接参与的专利已经被 Acoutechs 公司（由Armacell接管的声学材料制造商），Acoustic Sensing Technology 公司（对埋入式管道的声学检查）和nuron 公司（埋入式光纤电缆传感）进行了商业开发。

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记
Baidu
map