
在模拟辐射传热时,我们需要了解表面发射率的概念,它可能与温度、波长、角度和其他变量有关。在辐射传热系列博客中,我们将研究如何使用 传热模块对这些相关项进行建模,以及为什么它们对传热模拟很重要。
背景
普朗克定律是现代物理学的基本定理之一。它描述了一个已知温度下来自理想黑体的辐射光谱密度。我们可以使用普朗克定律来绘制自由空间中随温度升高的黑体光谱辐射功率。这表明,当温度升高,不仅发射增加,而且发射峰值会出现在较短的波长处。绘制与峰值发射率相关的归一化功率很有帮助。
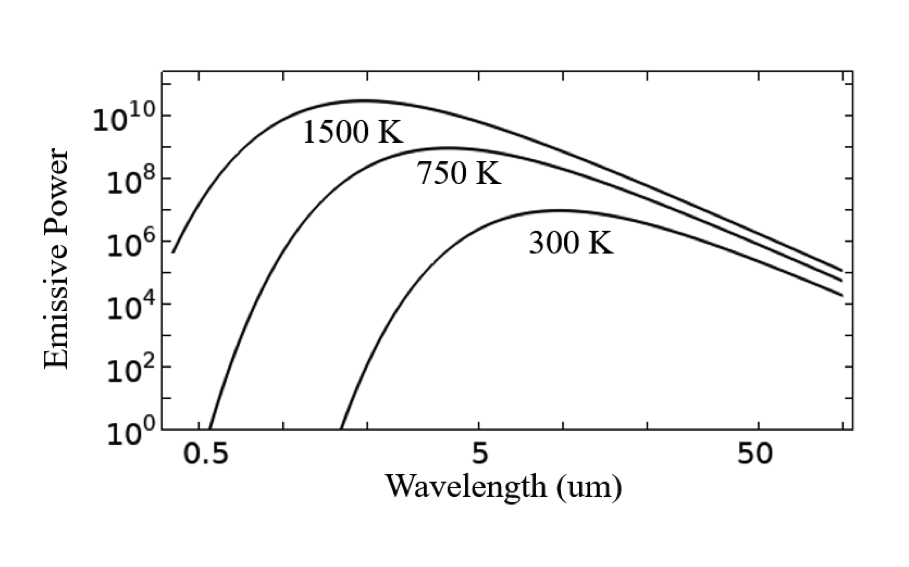
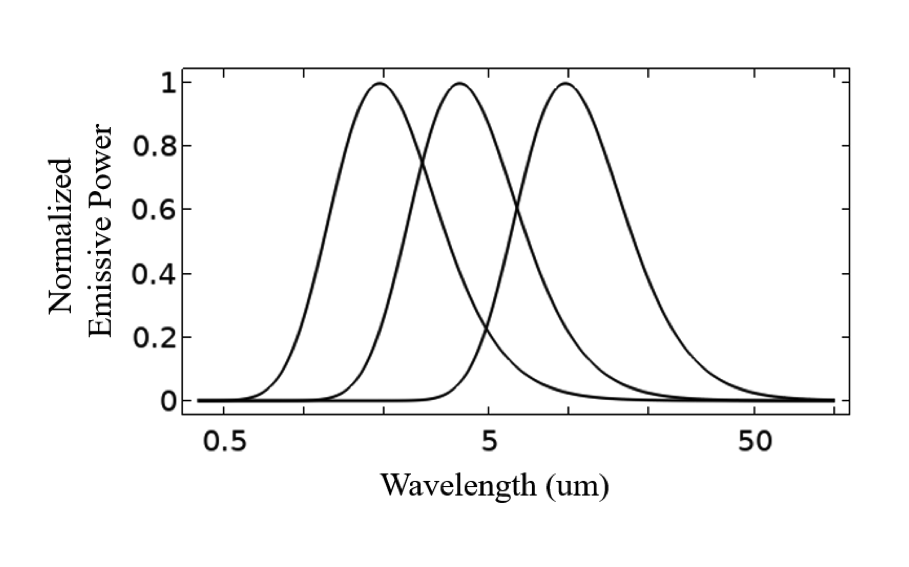
黑体发射功率的对数比例图(左),以及相对于峰值发射功率归一化线比例图(右),以对数尺度表示波长。
如果在所有波长范围内对普朗克定律进行积分,得到黑体在自由空间中的总发射率E_b = \sigma T ^4,其中\sigma是斯蒂芬-玻尔兹曼常数。现在,虽然黑体的概念肯定与工程相关,但所有材料都偏离了这一点,所以我们引入发射率的概念\epsilon,即在已知温度下材料的辐射与理想黑体的发射之间的比率。该比率必须始终在 0 和 1 之间,在这里我们仅讨论不透明材料的情况,在这种情况下发射是从材料表面辐射的。
虽然发射率通常被称为材料属性,但它是材料和表面形态的函数:与光滑表面相比,粗糙表面具有不同的发射率。一层薄薄的油漆、涂层或氧化层可以显著改变发射率,但对其他热行为的影响可以忽略不计。虽然经不同表面处理的常见工程材料有一些参考表格(例如,由 Incropera 和 DeWitt 编著的Fundamentals of Heat and Mass Transfer),但是在开始任何计算建模之前,收集覆盖完整工作条件范围的高质量数据是一个重要的步骤。在收集这些数据之前,细心的分析人员还应该知道哪些建模变量会影响发射率,以及这将如何改变建模程序。
最简单的建模方法是将发射率看作常数。这对于最大温度变化小于几十开尔文的工程应用来说通常已经足够了。然而,随着材料温度的明显变化,其材料特性也会发生变化,因此需要考虑发射率随温度的变化:\epsilon\left( T\right)。对于某些材料,发射率也会随波长\epsilon\left( \lambda\right)显著变化。尽管发射率会随波长连续变化,但是对于建模,将光谱划分为有限数量的离散波长带就足够了。这些波段的选择取决于被建模材料的发射率以及热环境。例如,如果考虑太阳能环境载荷,典型的做法是将波长分为两个波段,即太阳光波段和环境波段,但也可以考虑任意数量的波段。
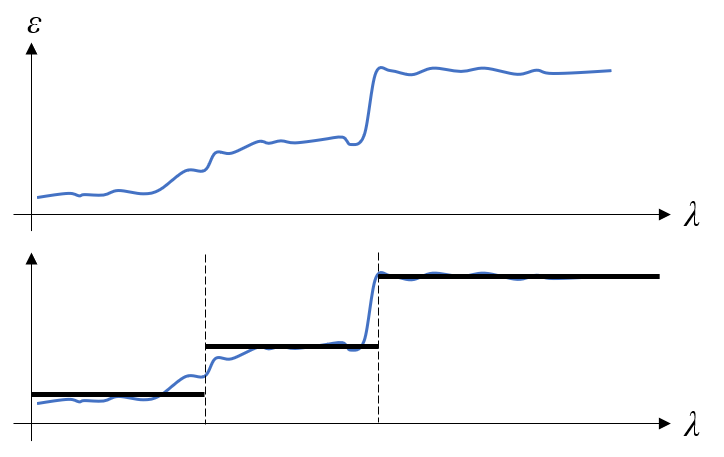
发射率与波长的函数示例(上图)。这种材料可以使用三个波段进行建模(下图)。
注意最左边或最右边的光谱带上的平均方法也很重要。与其对这些波段采用简单的平均发射率,不如根据预期温度范围引入加权更为合理;例如,忽略不考虑辐射波长上的发射率。在实践中,可能涉及许多不同的材料,因此在选择波段时,需要进行大量的工程判断和近似作为预分析步骤。
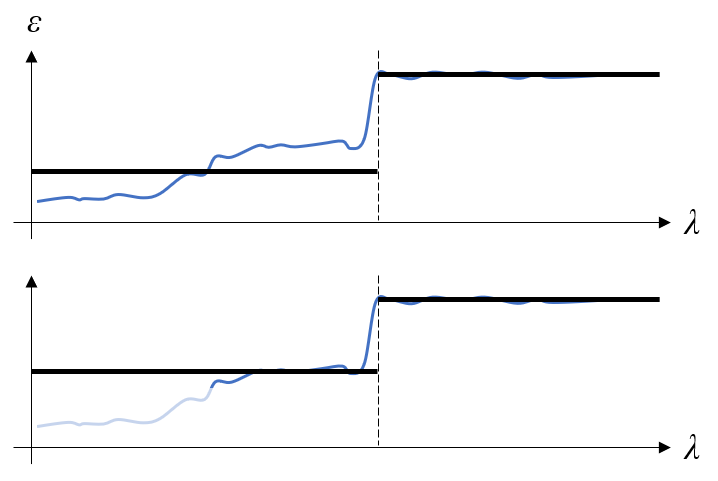
与波长相关的发射率被简化为双波段模型。在上图中,发射率只是在每个波段内取平均值。在下图中,未考虑左侧波段内极短波长的材料发射率。
发射率也可能随角度的函数而变化。尽管理想的黑体将在所有方向上等效的发射,但真实表面将与方向有关,通常仅与法线的角度有关,但在三维空间中建模时也可能与方位角有关。
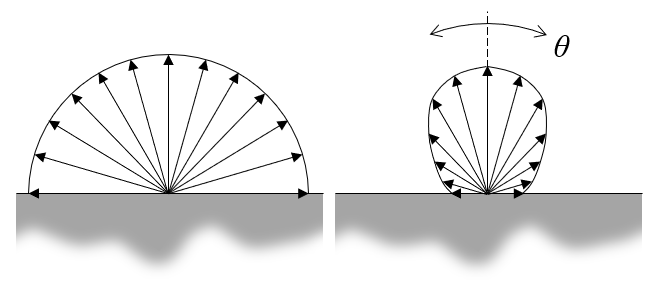
发射率可以是各向同性的,也可以与角度有关。
因此,发射率可能是温度、波长、极角和方位角的函数:\epsilon\left( T, \lambda, \theta, \phi\right)。此外,作为 COMSOL Multiphysics®软件接口的灵活性,您还可以将发射率设为与空间位置或任何其他模型变量相关的函数关系。同样重要的是,对于任何真实材料,发射率在所有波长和角度上的积分总是小于1。
接下来,让我们看看如何在 COMSOL 软件中对一些典型案例进行建模。
示例:零件冷却
以下图所示的简单零件为例来说明。一个热的材料样品位于一个圆形腔室的中心,该腔室壁保持在 0K 的固定温度。腔室内为真空,因此零件仅通过辐射散热冷却。我们想计算零件冷却的速度并观察入射到腔室壁上的辐射通量。假设腔室的壁是理想的黑体,因此它们可以被建模为具有单位发射率,并且由于它们处于 0K,这暗示了它们完美地吸收了来自零件的热辐射。
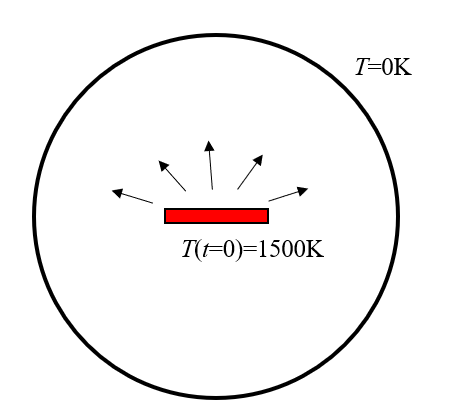
真空室内的热零件仅通过辐射散热冷却。
首先,我们考虑最简单的恒定发射率的情况。为此,我们采用与快速热退火案例模型的类似方法,使用表面对表面辐射传热接口建立了一个传热模型。此接口的默认设置假定单个波带并使用Hemicube方法计算角系数。
我们利用对称性仅对整个结构的 ¼ 进行建模,并为固体传热接口指定适当的热初始条件和边界条件,该接口仅在热零件的域内求解。表面对表面辐射接口在零件的暴露(非对称)边界以及腔室壁上处于激活状态。使用漫反射表面特征将腔室的壁建模为具有恒定的发射率 1,代表完美的吸收器。在漫反射表面特征中,我们还通过模型输入设置将壁温固定在 0K,如下面的截图所示。也就是说,我们固定了室壁的温度,这个特征提供了一种计算辐射热通量的方法。
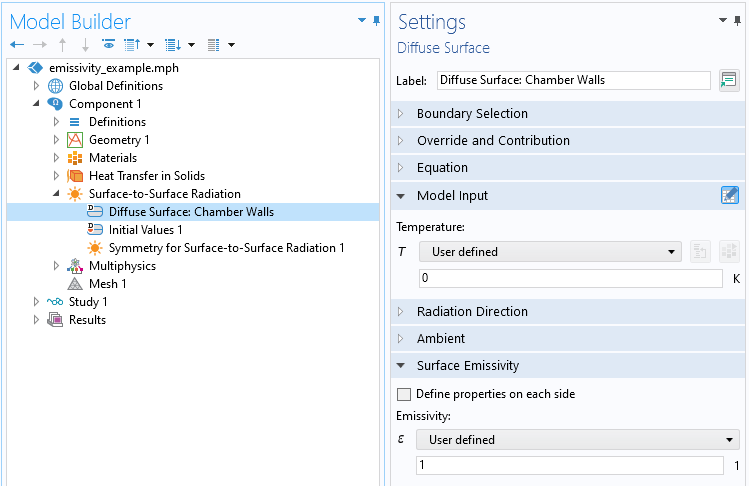
漫反射表面特征定义了腔室的壁。
现在可以关注对热零件本身的发射进行建模。首先,使用漫反射表面特征为样品指定恒定的发射率,如下面的截图所示。对于此边界条件,模型输入设置通过多物理场>表面到表面辐射传热特征定义了边界温度。也就是说,通过固体传热接口计算的温度定义了表面温度,通过表面对表面辐射接口计算的热通量对固体传热接口中的边界通量有贡献。
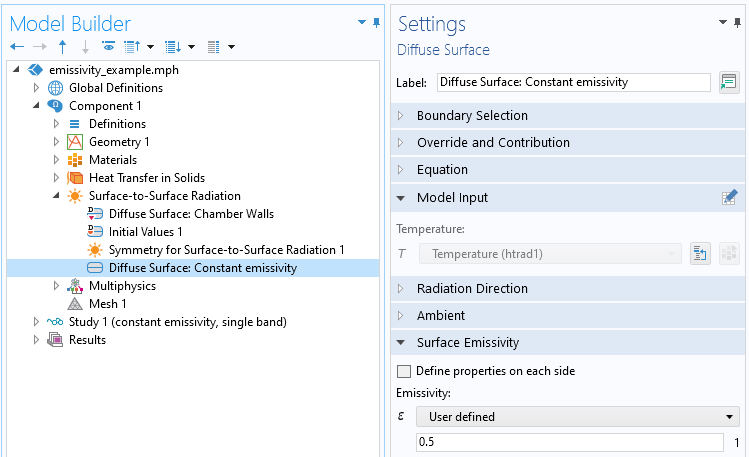
漫反射表面特征定义了零件的恒定发射率。模型输入部分反映了温度是通过固体传热接口定义的。
接下来,为了将发射率修改为温度的函数,最简单的方法是输入与温度变量有关的表达式,如下面的屏幕截图所示。也可以定义取决于温度的材料属性。
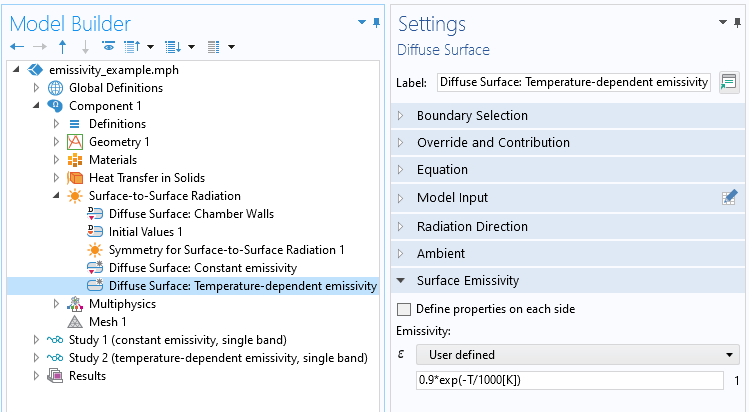
具有与温度相关的发射率的漫反射表面特征。
为了使发射率成为多个波段的函数,我们修改了辐射设置并指定波长来划分波段。在本例中,我们将只使用两个波段,如下面的屏幕截图所示,以 5 um 波长划分,并在每个波段上指定不同的恒定发射率。
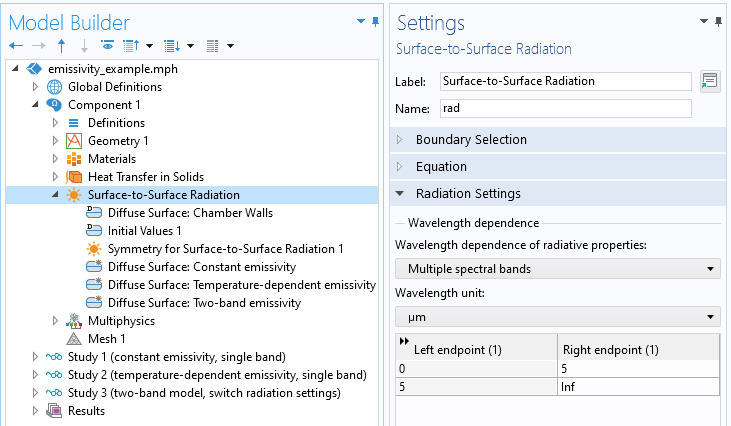
多光谱波段设置。
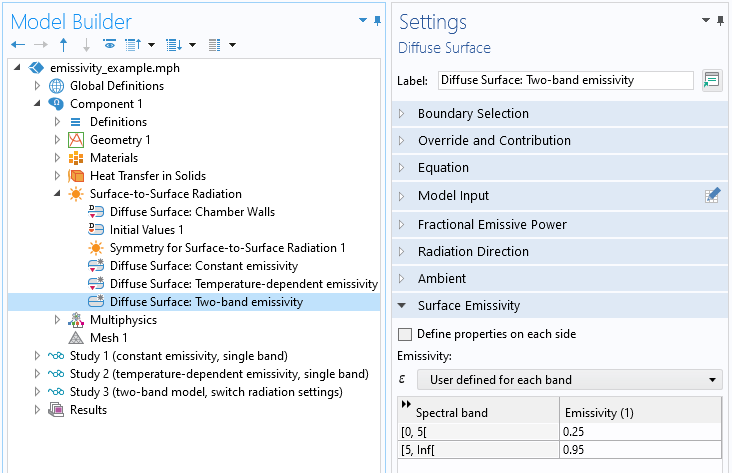
在每个波段内指定发射率。
最后,为了考虑随角度变化的发射率,计算表面对表面辐射的方法必须从Hemicube方法更改为射线发射方法。在下面的屏幕截图中,辐射模型被转换为单波段模型。
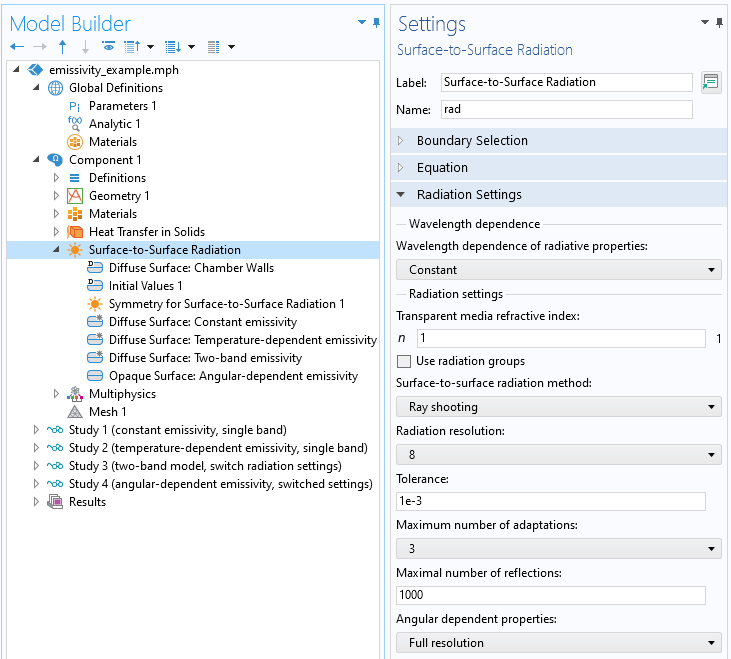
默认的射线发射方法设置。
使用射线发射方法时,也可以使用不透明表面特征。此特征提供了在整个表面上定义单个定向发射率函数的能力,该函数仅是角度的函数。然而,表面的总发射率通过表面发射率表达式定义,可以是温度T位置\mathbf{x}或任何其他变量的函数。总发射率是方向发射率函数和表面发射率表达式\epsilon_{tot} = \epsilon\left(\theta,\phi\right)+\epsilon\left(T, \mathbf{x}, …\right)之和:如果使用多个光谱带,则可以使用不同的表达式和函数。
不透明表面特征的设置。使用全局定义函数定义方向发射率。
所有这些不同的方法都会导致零件随时间变化的冷却曲线略有不同,如下图所示。就腔室壁的辐射通量而言,将恒定发射率与角度相关发射率进行比较也很有趣。
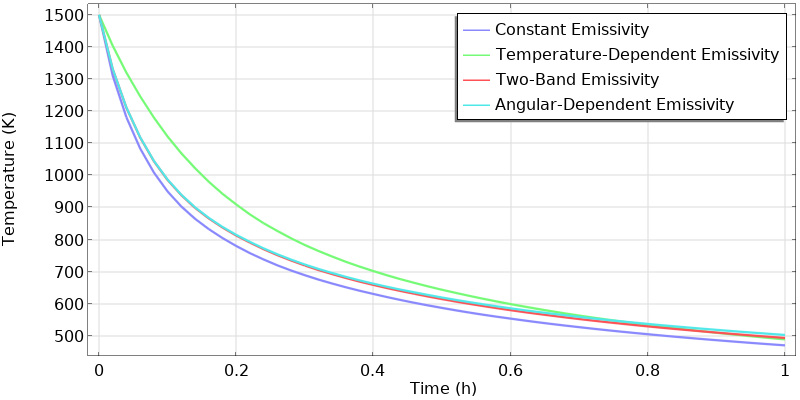
使用不同的表面发射率模型计算的恒定温度室中热零件的温度随时间变化曲线。
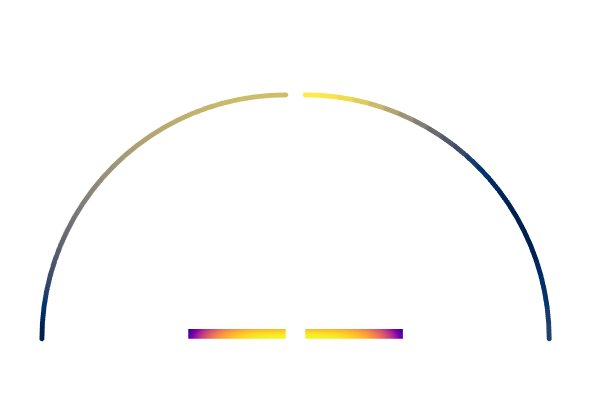
具有恒定发射率(左)与定向发射率(右)的热零件。绘制了腔壁上的通量,突出显示了发射辐射的方向性。
重要的是,在这个例子中,腔室壁在 0K 时是完美吸收体,没有热辐射返回到零件。为了完善我们对辐射传热的理解,了解热辐射撞击在非完美吸收体表面上会发生什么也很重要。这就是我们接下来要讨论的主题——敬请期待!



评论 (3)
三 张
2023-08-28这个例子可以发一下吗谢谢
Qihang Lin
2023-08-29 COMSOL 员工模型获取相关请联系技术支持://www.denkrieger.com/support
陈 小
2025-01-17谢谢您的帖子,我想了解comsol中是否可以通过方向发射率函数设置非对称分布的物体表面发射率?在我建模过程中,comsol似乎默认物体发射率是左右对称的(即发射率取决于0-pi/2范围内的定义,-pi/2-0的定义不起作用),实际上我想设置左右非对称分布的发射率函数,这在comsol中可以实现吗