
现在极受欢迎的单向组合乐队(1D乐队)和量子力学、宇宙学之间有什么关系吗?最近在悉尼歌剧院举办的一次演讲中,斯蒂芬·霍金很可能已经对此做出了解释。这涉及对平行宇宙的预测,也就是说,在无限多世界中,可能存在一个与我们完全相同、但存在各种可能的排列与差异的世界,就像是博格斯在《巴别图书馆》中提到的 410 页的书。
单向组合乐队的两个方向
在最近的一次活动中,有位提问者向斯蒂芬·霍金询问让世界上几百万少女粉丝都伤心不已的 Zayn 离开单向组合乐队的宇宙学隐喻。霍金的回答可谓相当精彩而又善解人意,他提出了一个理论物理学上的急转弯:“对这些伤心的姑娘们,我的建议是去密切关注理论物理方面的研究。因为某天,我们也许会证明多个宇宙的存在。在我们自己宇宙之外的某处,并非完全没有可能存在另一个不同的宇宙,在那个宇宙中,Zayn 还会留在单向组合乐队。”
继续分析霍金的回答之前,让我们先来看一下两个有关平行宇宙预测的令人振奋的理论。
量子世界
在量子力学中,通过波函数(即薛定谔方程的解)的线性组合,将能得到有关基本粒子时间及空间位置的概率函数。例如,由电子密度波函数得到原子和分子的轨道概率函数。
让我们来分析一下薛定谔方程中针对氢原子的公式示例:

包括由 ψ 表示的波函数的瞬态薛定谔方程 (1)。对于确定的能量态(2),我们可以利用时谐形式重写,因此得到 (3)。电子的势能 V 仅依赖于半径,可以在球坐标中编写波函数 (4)。不同能级的波函数 En,可以表示为球面谐波 (Yl,m) 和幅值 (Fl) 的乘积,其中,I 表示总角动量的量子数,m 表示角动量的 z 分量。在球坐标中求解薛定谔方程 (3),得到波函数 (4)。

单电子的波函数称为轨道。波函数的线性组合(叠加)也就是薛定谔方程针对氢原子的解。量子数 l = 0 的轨道呈现球面对称。l = 1 的轨道表示为 p 轨道,表现出明显的角依赖性。l = 2 的轨道叫做 d 轨道,表现出了更复杂的角依赖性。绘图显示了一些波函数的等值面。
通过类似的方法,物理学家和物理化学家已经能够计算宇宙中可能存在的稳定元素的元素表。
对粒子位置和时间的测量与一种不确定性有关,即所确定的粒子位置越精确,所能确定动量的精度越低。这叫做海森伯不确定性原理,以提出这一理论的科学家命名。例如,如果我们精确获知了粒子的位置,就无法确定它在同一时刻的动量。
在量子力学中,会在观察到位置或动量的时刻发生波函数坍缩。这也可以通过当粒子与其环境发生相互作用时产生的相干脱散来解释。也就是说,当测量粒子时,无法使用波函数对其进行描述(或由于相干脱散的关系,无法再对其进行描述),我们仅能在一个位置上找到粒子。
但最初由埃弗雷特提出对量子力学的多世界解释,否定了波函数的坍缩。相反,它推导出可能存在多个平行宇宙,表示了波函数所有可能的线性组合(叠加)。“宇宙”可能是非常多个平行宇宙或量子世界的量子叠加,它们之间可能并没有交流。
永恒膨胀
根据膨胀理论,“大爆炸”源自于一块极小物质的暴涨,该物质的体积远小于一颗原子。这一小块物质的密度恒定,质量每隔 10-38秒增加一倍。大约 260 次之后,也就是说经过 10-35秒后,质量达到了我们整体“宇宙”的质量。
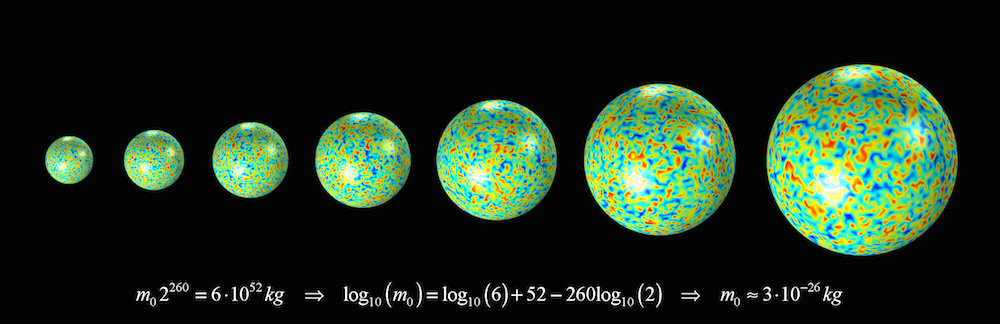
膨胀期间,小块物质的质量和体积不断翻倍,并从反重力中得到能量,形成新的质量,同时伴随着量子涨落。由于海森伯不确定性原则,形成一种结构,后续发展成为我们“宇宙”的宇宙结构。这一小块的质量大约是 3·10-26kg。您可以对比一下这一质量与氢原子的质量,后者为 1.7·10-27kg!
回想一下公式 E = mc2,用于形成质量的能量源自于膨胀物质所产生的反重力,其中所消耗的能量刚好能够使恒定密度物质的质量增加一倍。鉴于“宇宙”的总质量大约是 6·1052kg,也就是说,重力最后会拥有相当大的能量。相比之下,在长崎投下的原子弹仅将 1 g 的质量转化为了不同的能量形式。这可以解释为什么重力的能量为负,也就是说,我们需要作功才能将依靠重力吸引在一起的两个物体分开。
从永恒膨胀预测到,我们所谓的”宇宙”只是无限宇宙中无限多哈勃体积中的一个,所谓哈勃体积是由永恒膨胀产生。这些哈勃体积类似于我们的哈勃体积,但拥有不同的宇宙结构。在膨胀的早期阶段,量子效应会造成宇宙种子的涨落,这一涨落又促进了我们的哈勃体积宇宙结构的形成。空间中的一些区域现在包括一些比单个原子还要小的星系,其中量子效应是相关的。在这一维度上,宇宙的种子涨落就可以由海森伯不确定原则解释,它会阻止任何物质出现均一性,包括膨胀物体。

在无限宇宙所包含的无限数目的哈勃体积中,一些哈勃体积可能与我们称之为“宇宙”的哈勃体积完全相同或几乎完全相同。
与我们的哈勃体积相比,大多数哈勃体积中的物质分布不同,但由于存在无限多哈勃体积,也可能存在无限多的哈勃体积的变体,它们拥有着相同的物质分布。也可能存在近乎无限数量的世界变体,它们与我们的世界完全相同或几乎完全相同。
统一多元宇宙
对量子力学的多世界解释将带来近乎无限数目的宇宙,也表示了近乎无限数目的 MIT 宇宙学家 Max Tegmark 所称谓的第三级平行宇宙。同样,膨胀理论也可能预测了无限数目的哈勃体积,形成根据《Our Mathematical Universe》一书的作者 Tegmark 所描述的第一级平行宇宙。
因此,可能存在无限数目的第一级平行宇宙的变体,它们包含与我们的“宇宙”相同的元素数目,但排列方式不同,因为波函数和量子涨落可能产生无限数目的组合方式。从这个意义上讲,Tegmark 预测到,第三级平行宇宙和与之几乎完全相同的第一级平行宇宙可能是一个,并且完全相同,所以一个系统的波函数可能会描述它在空间中的无限复本。
霍金对 Zayn 离开单向组合乐队的看法
人们一直热衷于就量子力学的多世界解释及膨胀理论展开幻想。
最近,斯蒂芬·霍金通过全息影像的方式参加了悉尼歌剧院的一次活动,一位采访者向他提出了以下问题:“Zayn 离开了单向组合乐队,让世界各地的无数少女们都伤心不已,您认为它的宇宙学影响是什么?”
霍金的回答可以被解释为引用了膨胀理论、均匀性,以及量子世界:“对这些伤心的姑娘们,我的建议是去密切关注理论物理方面的研究。因为某天,我们也许会证明多个宇宙的存在。在我们自己的宇宙之外的某处,并非完全没有可能存在另一个不同的宇宙,在那个宇宙中,Zayn 还会留在单向组合乐队。”
我们利用下面的示意图来解释霍金的回答。在这个世界中,Zayn 离开了这个乐队。但在第一世界中,Zayn 还留在乐队中,这个世界中的所有人都不知道他离开这件事。在第二世界中,Zayn 不仅留在了乐队中,还娶了一个在这个世界中因为他的离开而伤心不已的姑娘。不仅如此,在数以百万计的其他世界中,从 n=3 到 n=100 万,他都娶了一个在这个世界中因为他的离开而伤心不已的姑娘。
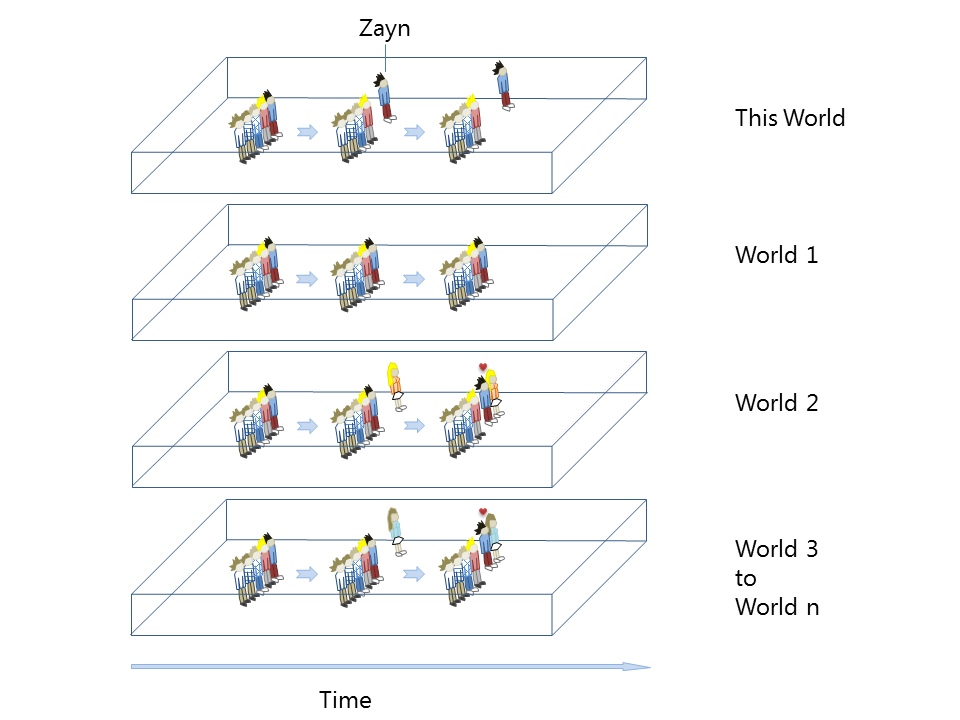
在可能存在的数以百万计、且近乎无限世界中,Zayn 不仅留在了乐队,还娶了一位在这个世界上为他伤心不已的姑娘。
量子世界和无限数目的哈勃体积都可以被解释为对 Jose Luis Borges 的《巴别塔的图书馆》的类比。图书馆中收藏的 410 页的书可以是对所有可能的几乎完全相同的量子世界或第一级平行宇宙的类比,它们有着相同的哈勃体积和物质量(410 页),我们将它称作我们的“宇宙”。在这些世界中的任意一个,所有你曾想过的那些故事最终都可能发生!
多物理场仿真
同时,和霍金的建议一样,我们给这些单向组合乐队的伤心粉丝们的建议是:选择学习科学,然后借助多物理场仿真开发出的各种仪器与设备来研究薛定谔方程的解和膨胀理论,就像下图演示的那样。
幸运的是,第一级和第三级多元宇宙中的物理定律与我们的相同,在所有的哈勃体积及所有的第三级宇宙中,您都可以通过 COMSOL Server 的全球网络许可证来运行仿真 App,模拟薛定谔方程。
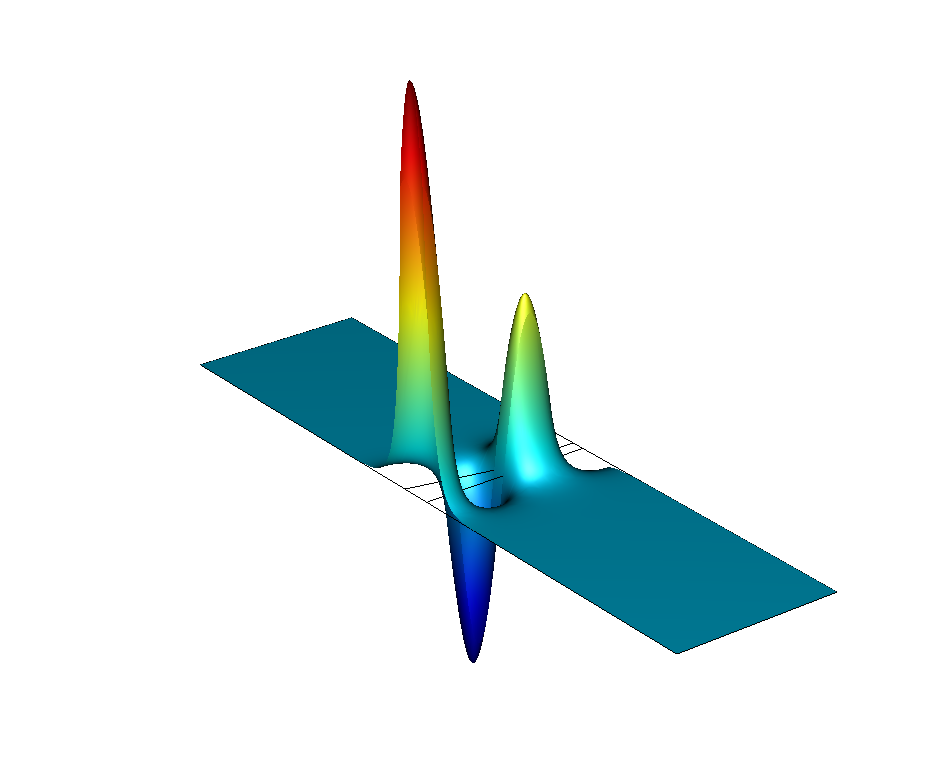
锥形砷化铟量子点模型的仿真结果,显示了电子能的波函数。为了计算量子点的电子状态,我们求解了1-频段薛定谔方程。
推导出另一个(或多个)平行宇宙之前,Zayn 仍是单向组合乐队的一员,这些姑娘们也许还能开发出一些相当令人振奋的东西,比如用于量子计算机或生物标记的量子点。她们也许还能设计和开发出用于深太空探索、以及研究这一个我们称之为“宇宙”的哈勃体积中的星系。
在其中的一个世界中,单向组合乐队的一名粉丝可能会是或者即将成为宇宙中最强大的多物理场软件的创始人和开发者!不过,这会在什么时候以及哪个世界出现呢?

在另一个世界中,斯蒂芬·霍金可能是剑桥的一位牧师,正主持 Zayn 和一位单向组合乐队粉丝的婚礼。在这个世界中,英国人可能在讲中文,中国则在讲英语,不过他们会把它叫做“中文”。
有关多物理场仿真空间应用的扩展阅读
- 仿真帮助改进了载人航天器中的大气再生系统
- 超材料把物理变成了魔术
- 来自 NASA 的 Ed Ethridge,借助 COMSOL Multiphysics 从月球中提取水
- 使用 COMSOL 模拟火星漫游者中的传热,用于保护设备仪器
- 罗罗塞塔号和菲莱号:在彗星表面的历史性着陆
- William T. Vetterling:COMSOL Multiphysics 与巴别塔图书馆(COMSOL 年会的主题演讲视频)



评论 (0)