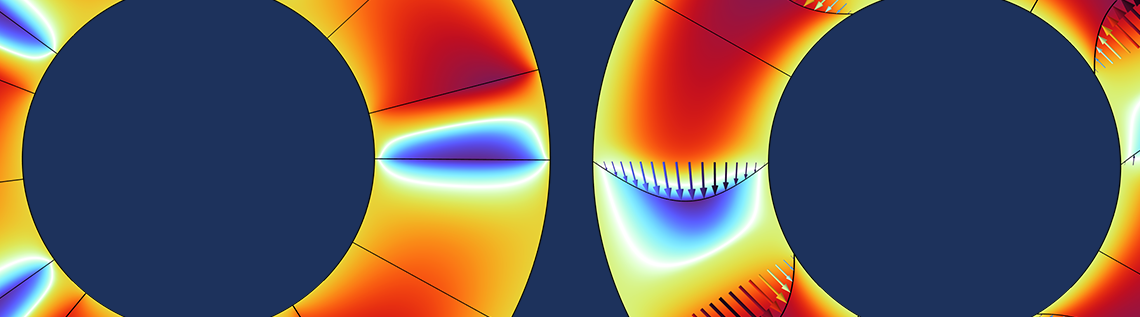
立式推力轴承用于支撑旋转机械中的轴向载荷，由于承载能力取决于几何形状，因此可以通过形状优化和拓扑优化来最大限度地提高轴承的承载能力。形状优化通过改变轴承中阶梯的形状来实现，而拓扑优化则使用隐式几何描述，因此阶梯的数量可以变化。
简介
在建立立式推力轴承模型时，我们假设:
- 液膜厚度远小于轴承横向尺寸
- 与润滑油薄膜造成的剪切效应相比，惯性效应可以忽略不计
- 体力可忽略不计
- 润滑剂为牛顿流体
- 由于油膜的长宽比很大，面外速度可以忽略不计
- 速度大小取决于面外坐标的分析结果
假设 2–4 成立表示纳维-斯托克斯方程可以简化为斯托克斯方程，假设 5–6 成立则使我们能够进一步假设流体速度与压力梯度成正比。考虑到这几点以及其他假设，控制方程可以简化为标准的雷诺方程，但为了考虑气蚀问题，本文使用的是 Jakobsson–Floberg–Olsson (JFO)理论。您可以从下面的压力分布草图中看到这一点。当流体通过收缩处时，压力逐渐减小，直到接近下一个阶梯的凹槽时才开始增大。
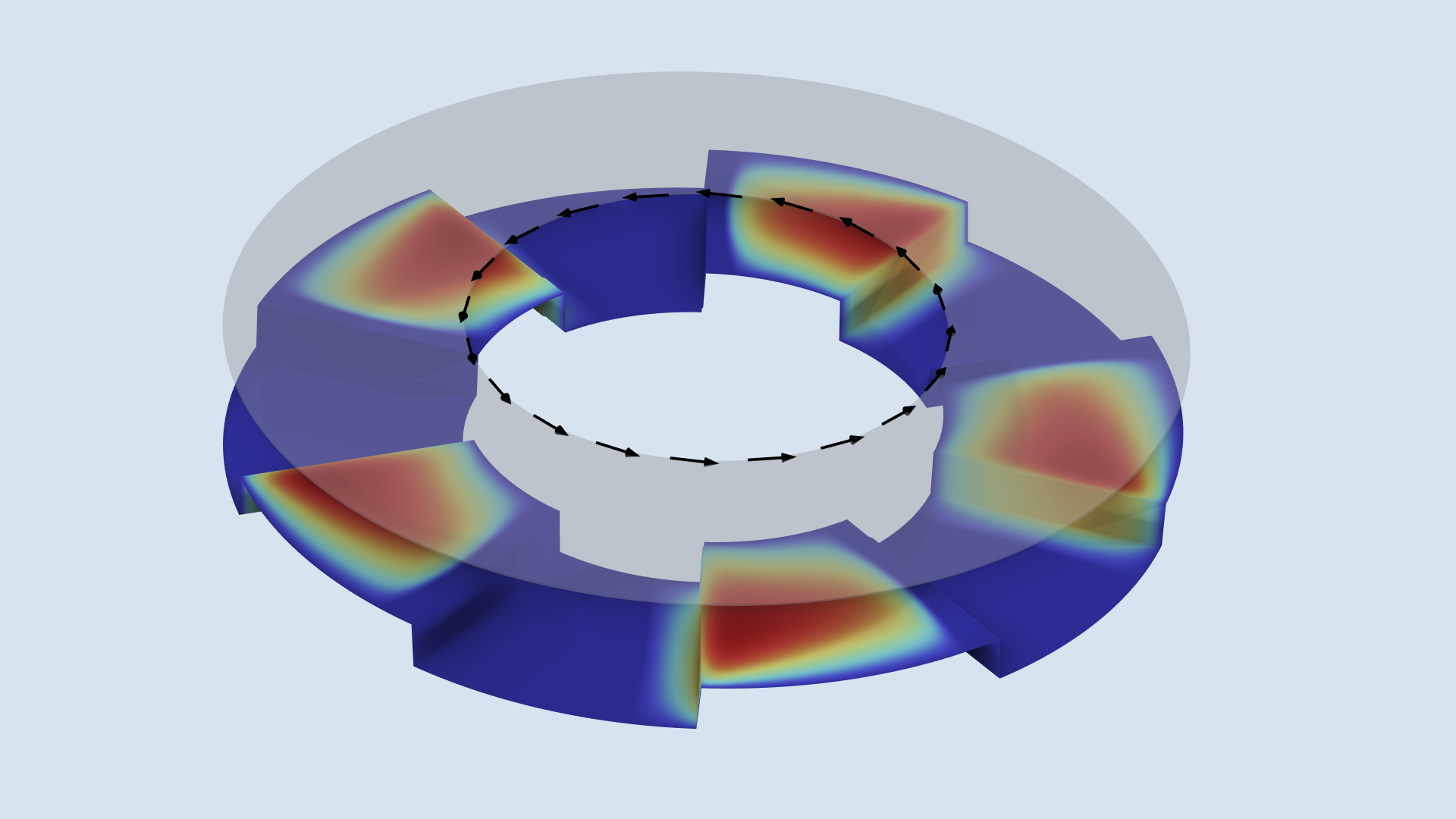
带轴环的立式推力轴承简图。颜色表示压力。请注意，阶梯并没有明确的三维模型，因此该图并不代表计算网格。
采用 COMSOL Multiphysics® 软件中的液体动压轴承 接口模拟轴承的物理场。这个功能没有明确考虑面外尺寸，而是使用平面几何代替，并在方程中直接考虑厚度变化，如上图所示。
承载能力取决于压力分布，而压力分布又取决于阶梯的形状。因此，应用形状优化来最大限度地提高承载能力是合理的，
其中，\boldmath{f}_\text{c} 是作用在轴颈上的分布力，由泊肃叶（Poiseuille）压力、库埃特（Couette）压力和法向压力分量组成。如前所述，该模型考虑了气蚀，但没有尝试限制气蚀的严重程度。
形状优化
形状优化通过网格变形来改变现有形状。在形状优化 接口中，有许多内置函数可以实现这个操作，本文的示例中使用了三阶多项式壳 特征，其中禁用了面外变形。在一组瓦的前边和后边上应用此特征，并使用扇区对称 特征将网格变形复制到其他瓦上。
这里演示的方法将点的位置固定在圆形边界上，但也可以让这些点沿着圆形边界滑动。不过，这需要使用基于方程建模，并分别在阶梯的后边和前边上应用 控制函数 特征，但这样会使设置变得复杂。设计自由度的提高只能略微优化性能，因此本文将重点研究更简单的方法，COMSOL® 6.1 版本的案例库中内置了一个替代案例，您也可从 COMSOL 官网的案例下载页面下载。
形状优化的结果如下图所示。结果取决于边的最大变形量和初始凹槽角度。优化后的设计在将油压到瓦上之前，先将油推到中间。
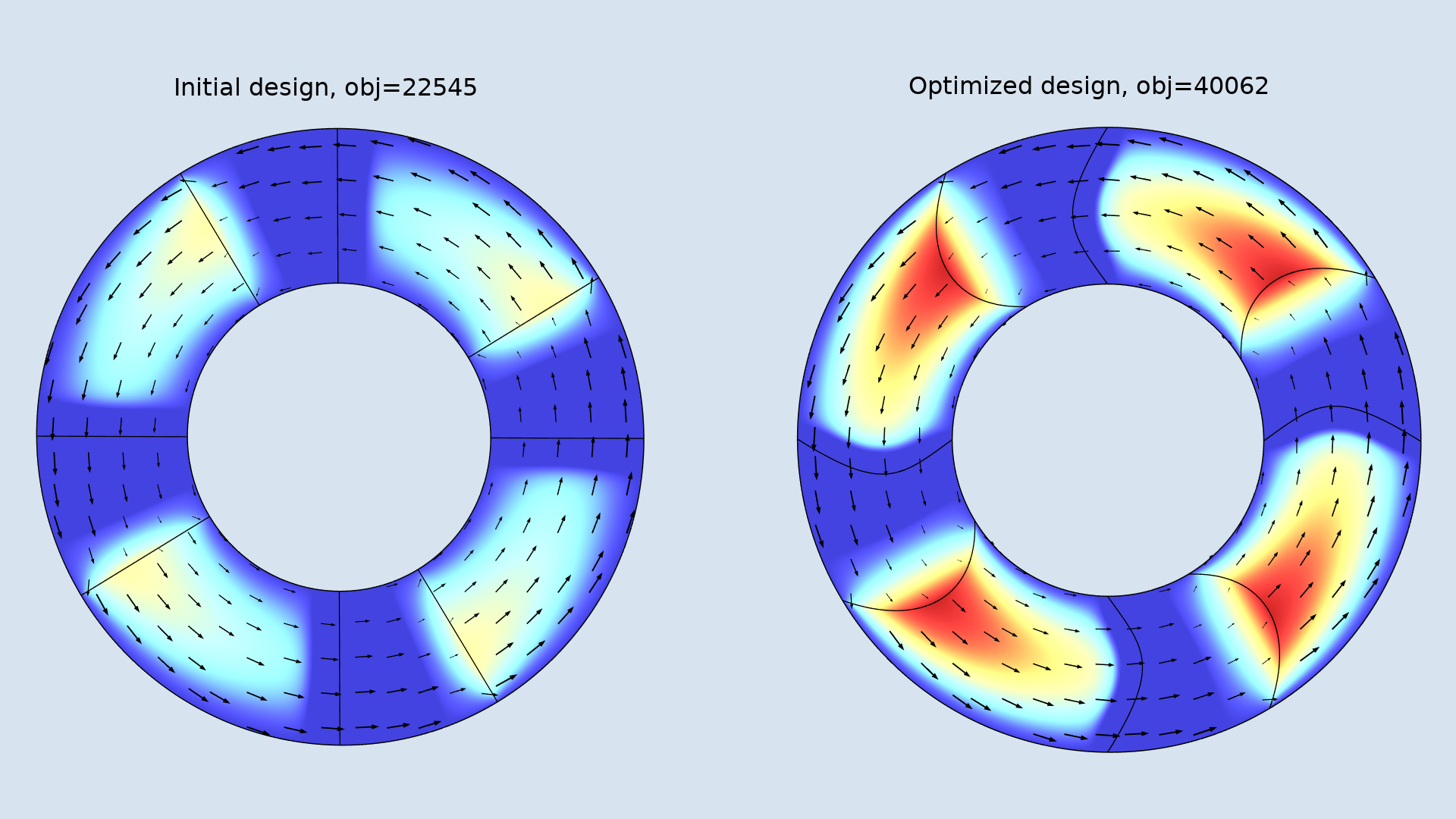
图中显示了初始设计（左）和优化设计（右）。图中箭头表示平均流体速度，颜色表示压力分布。
在变形设置中通过重新划分网格进行验证是一种较好的做法。从COMSOL案例库中此模型的演示中可以看出，验证并未发现任何数值问题。
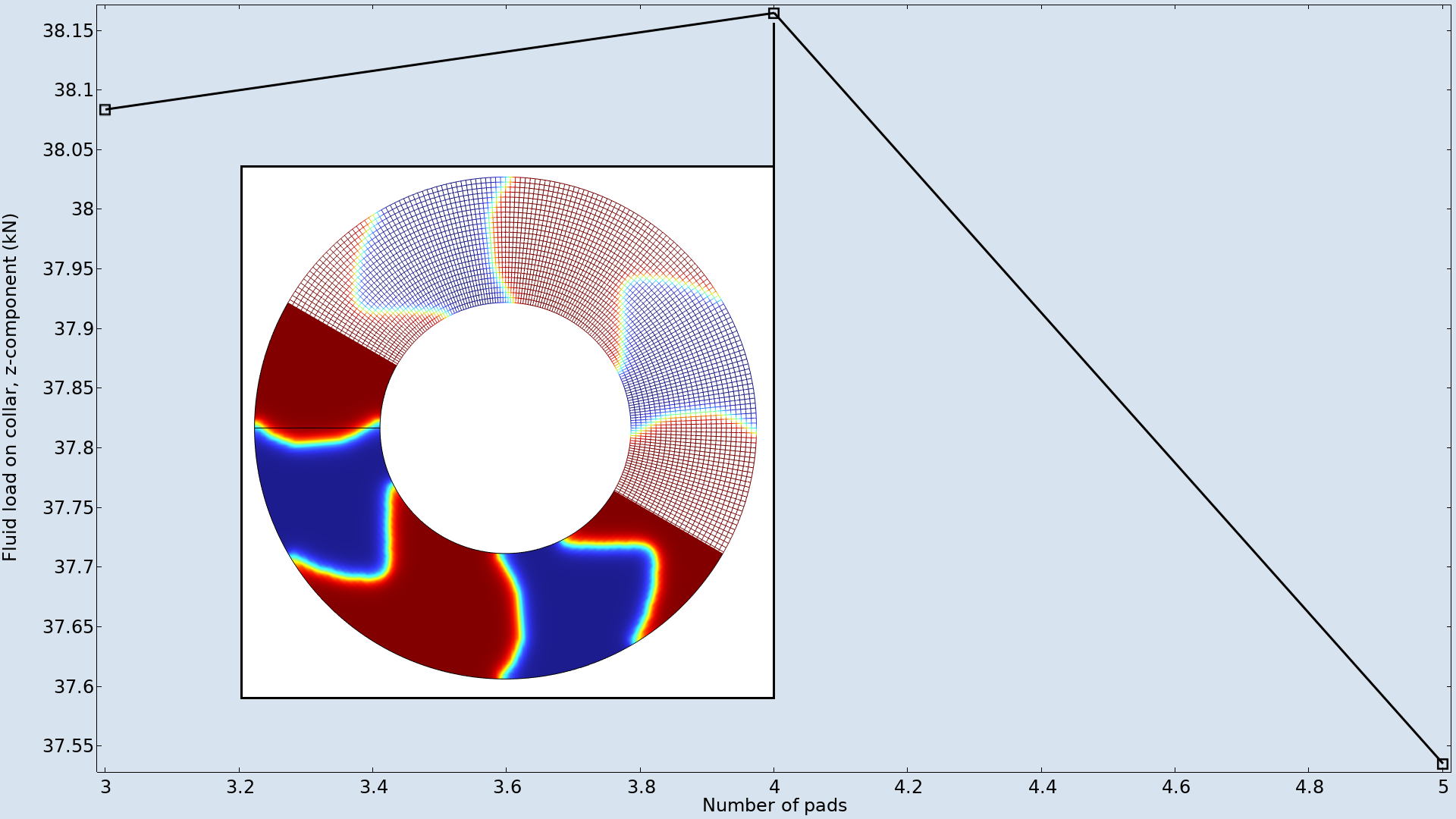
在本示例中，最大变形和沟槽角度被固定为与瓦数量无关。因此，最佳瓦数量为4个，如下图所示。
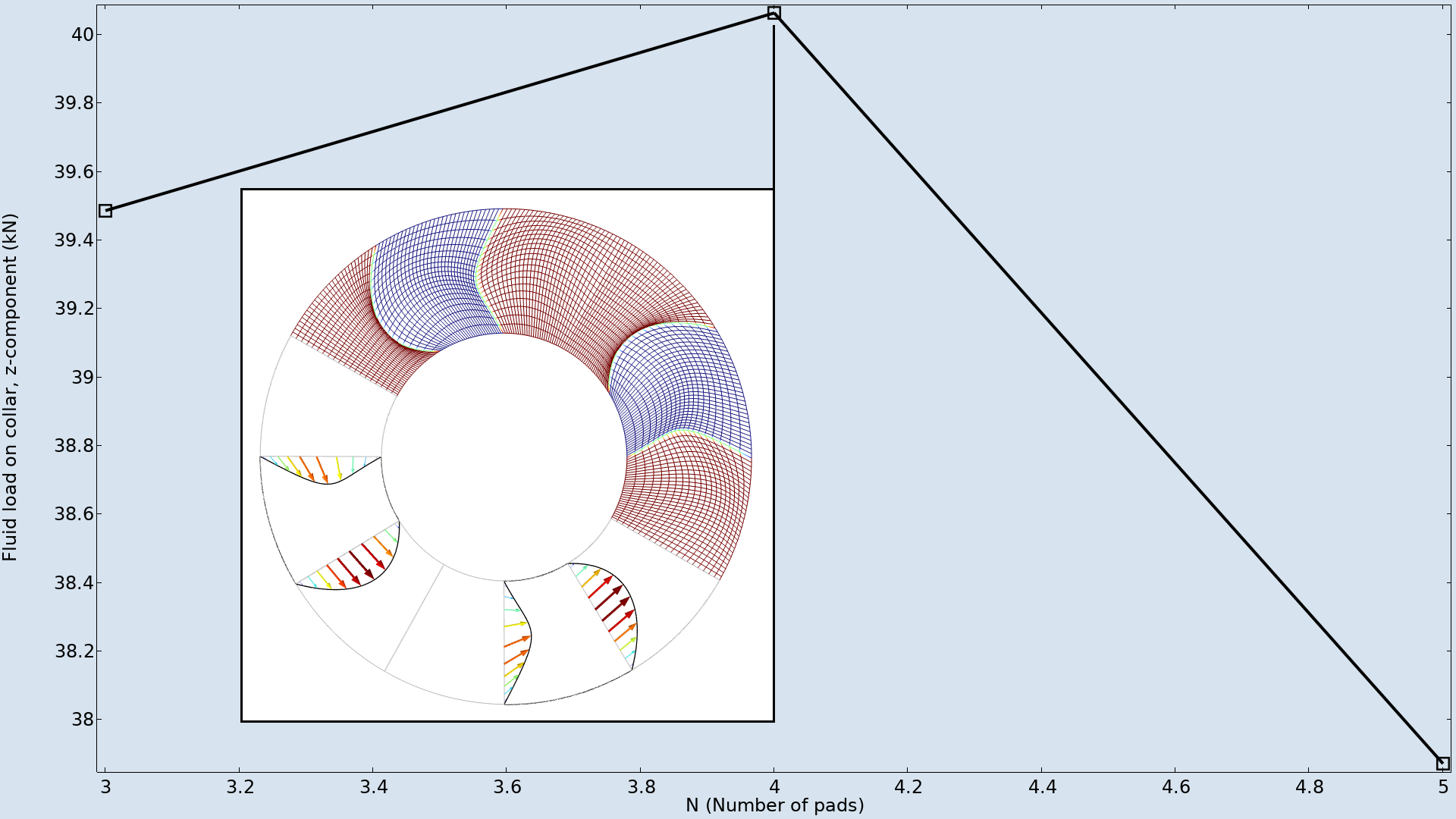
对不同数量的瓦进行形状优化，并将优化后的目标绘制成图。当瓦数量为4时，出现最大值，插图显示了网格的变形情况。
无论采用哪种物理方法，形状优化的工作原理都是一样的，因此很容易设置仿真。为了避免数值问题，形状优化引入的网格变形是有限的，但您可以自由尝试在大设计自由度与高性能优化，以及小设计自由度与稳健优化之间取得平衡。无论如何，优化设计在很大程度上依赖于初始几何图形，拓扑结构（以及阶梯数）只能作为优化的输入，而不是输出。拓扑优化通过引入对几何图形的隐式描述来解决这一问题。这种方法可能有其自身的缺点，但在这个示例中，使用拓扑优化方法不会带来任何明显的复杂性。
拓扑优化
拓扑优化是通过为每个计算单元引入一个与物理量相关的设计变量 \theta_c 来实现的。该变量被限制在 0 和 1 的封闭区间内：
- 当设计变量等于 0 时，求解与凹槽相对应的控制方程
- 当设计变量等于 1 时，求解与瓦相对应的控制方程
- 当设计变量介于 0 和 1 时，求解的是将凹槽和瓦的方程结合在一起的控制方程
凹槽和瓦之间的唯一区别在于油膜厚度 h_f，因此只要让油膜厚度取决于设计变量，就能满足上述要求。对于其他拓扑优化问题，第三点需要特别注意的是细节，但在本例中，简单的线性插值就足够了。
其中，\theta_f 是物理场，而\theta_c是控制变量场。在这个示例中，可以设置 \theta_c = \theta_f，但可以通过引入滤波器来去除控制变量场中的小尺度长度来改善收敛性。这样做还能为结果评估和验证提供更平滑的结果。滤波器可用下列偏微分方程（亥姆霍兹滤波器）表示
其中， R_\mathrm{min} 是最小尺度长度。(有关拓扑优化的亥姆霍兹滤波器和正则化的更多详细信息，请参阅博客：通过密度方法进行拓扑优化。
优化可以自由地将设计变量设置为中间值，在这个示例中，我们可以将其理解为中等油膜厚度，但中间值通常没有明确的物理表示，或者至少没有实际意义。从优化自动找到一个没有中间设计变量的解的意义上来说，这个问题似乎本身就很好解决，也就是说瓦和凹槽之间有明显的区别。
拓扑优化最好从设计变量的均匀值开始。如下图所示，这样的设计有4个瓦，但也可以从非均匀设计开始，以获得不同的局部最优值。
采用不同的非均匀初始设计对拓扑优化进行初始化，以生成某些拓扑结构。图中显示最优瓦数量为 4 个。
对于这些设置，形状优化和拓扑优化结果非常一致。
在进行拓扑优化后，验证仿真也是一种很好的实践，但形状优化验证的目的是检查与变形单元相关的数值问题，拓扑优化验证的目的是检查与隐式几何表示相关的问题。因此，拓扑优化验证使用的是显式几何表示法，其目标函数明显更好，这表明隐式几何描述需要大量计算成本。进一步探索发现，如果使用更精细的网格，拓扑优化的目标函数会明显更好，如下面的动画所示，该设计初始化时采用了 16 个瓦的拓扑结构。由此产生的设计与之前的设计在质量上相似，类似与人字形槽推力轴承。
对初始含 16 个瓦的轴承进行拓扑优化。
所有优化都考虑了固定的旋转方向，这一点在优化设计中清晰可见。初始设计相对于旋转轴是对称的，因此，放宽这一限制显然可以提高性能。正因为如此，如果在优化中同时考虑两个旋转方向，预计目标也会变小。
结语
在这篇博客中，我们讨论了如何利用形状优化和拓扑优化设计立式推力轴承。文章讨论的物理场和优化设置可以通过下列模型及其相关文档进行验证：
进阶学习
您可以查看以下资源了解更多有关优化的信息：
- 阅读以下附加模块的功能，使用这些模块可以优化立式推力轴承（以及更多其他轴承！）:
- 阅读下列博客，了解有关结构力学拓扑优化的更多信息:
评论 (0)