Today, room acoustics simulation is an essential part of designing good sound, whether it’s creating an immersive virtual scene, designing a comfortable acoustic environment in a room, or optimizing an audio experience. The Acoustics Module, an add-on to the COMSOL Multiphysics®software, includes several interfaces that are well-suited for room acoustic simulation. This blog post will focus on the importance of sound-absorbing boundary conditions for room acoustics modeling.
Sound Absorption Performance
To understand the sound-absorbing boundary condition, we will first address the sound absorption coefficient. To express the absorption characteristics of absorbers, the following three quantities are used (Ref. 1):
- Sound absorption coefficient,\alpha: the ratio of nonreflected sound energy to incident sound energy
- Specific acoustic impedance,Z_{\rm n}: the ratio of sound pressure to the normal particle velocity on the surface of the sound absorber
- Complex pressure reflection coefficient,R: the ratio of reflected sound pressure to the incident pressure
We now analyze these parameters by the ideal situation that the plane wave enters the porous absorber, which is described below.
 Plane wave incident to the porous material.
Plane wave incident to the porous material.
Here, the wavenumbers for air and porous material are assumed to bekandk_{\rm e}, respectively. The incident, reflection, and transmission sound pressures arep_{\rm i},p_{\rm r}, andp_{\rm t}. The incident, reflection, and transmission angles are\theta,\psi, and\phi. The amplitudes of incident and reflection sounds are represented byA_{\rm i}andA_{\rm r}, and lastly,B_{\rm t}andB_{\rm b}represent traveling and backward sounds in the porous media. The porous absorber with a thickness ofdm was assumed as the equivalent fluid (see ourMultiphysics Cyclopedia) for more information. The termination with rigid boundary was set tox=d.
From the linear acoustic wave equation, the particle velocity in x direction of the incident, the reflection, and the transmission sounds, which are respectivelyv_{\rm i},v_{\rm r}, andv_{\rm t}, can be expressed as:
Here,Z_{\rm 0}andZ_{\rm C}represent the characteristic impedance of the air and the porous material. From the definition, the reflection coefficient is written as follows:
On the interface boundary between the air and porous layer (x=0), the following two continuous conditions are posed:
With these continuous conditions and Fermat’s principle,\theta=\phi, the specific acoustic impedance can be expressed as follows:
Thus,
The absorption coefficient can be determined with the next equation.
Thus, you can model the sound absorption on boundaries by assigning one of three quantities to boundaries. Also, the above equation shows that\alphais inherently incident-angle dependent.RandZ_{\rm n}are complex parameters that include phase information, while\alphais an energy parameter. The phase information is important to accurately simulate the room modes. Therefore, the complex parameters are generally better inputs for wave-based room acoustic simulations. On the other hand, the sound absorption coefficient is good for reading the absorber’s performance intuitively, and is the main output in the sound absorption test. The random incidence absorption coefficient, which is the averaged value over solid angles, is taken as the practical performance of absorbers.
In the following equations, we further investigate the acoustic impedance of the porous material.
The transmission pressure and velocity atx=0are as follows:
On the other hand, those atx=dare as below:
With these equations, we can express the parameters at the inlet with terminal values using the following matrix form:
p_{\rm t}(0) \\
v_{\rm t}(0) \\
\end{bmatrix}=\begin{bmatrix}
\cos{(k_{\rm e}d\cos\phi)} & j\frac{Z_{\rm C}}{\cos\phi}sin{(k_{\rm e}d\cos\phi)} \\
j\frac{\cos\phi}{Z_{\rm C}}sin{(k_{\rm e}d\cos\phi)} & \cos{(k_{\rm e}d\cos\phi) \\
\end{bmatrix}
\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}={\bm T}_{\rm F}\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}
Here,{\bm T}_{\rm F}is the transfer matrix of fluid layer, which has been widely used for modeling sound absorption and insulation using the transfer matrix method (TMM) (Ref. 2). With the Snell’s rule ofksin\theta = k_{\rm e}\sin\phi, we can rewrite{\bm T}_{\rm F}with the form below:
\cos{(k_{\rm n}d)} & jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}sin{(k_{\rm n}d)} \\
j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)} & \cos{(k_{\rm n}d) \\
\end{bmatrix}
Here,k_{\rm n}=(k_{\rm e}^2-k^2\sin^2{\theta})^{\frac{1}{2}}. Under the rigid boundary condition on the terminal (v_{\rm t}(d) = 0), we can calculate the specific acoustic impedance of the porous absorber as follows:
The above equation indicates that the specific acoustic impedance itself is angle dependent. Thus, to fully model sound absorption at a boundary, the angle dependence of the absorber impedance should be taken into account.
Local and Extended Reaction Models
When modeling sound absorption at boundaries, two types of absorption boundary models are adopted — local and extended reaction models. The local reaction model, a standard in room acoustics simulation, uses the angle-independent impedance (generally using the impedance value of the normal incident condition) to describe the sound absorption property of the boundary. It is assumed that the particle velocity at a given point on the absorber’s surface is independent of the behavior at other points on the surface. The extended reaction model adapts the angle-dependent impedance. Of course, the local reaction model is approximate, but it is efficient and works well for modeling the sound absorber whose acoustic impedance has little angle dependence, such as rigidly backed porous materials with high flow resistivity and the absorbers with honeycomb core. The extended reaction model is accurate, but it generally requires additional modeling of the absorber interior. To achieve accurate and efficient room acoustic modeling, you should choose an appropriate absorption boundary model to the absorber installed in rooms. Below, the effect of the absorption boundary type on the random incidence absorption coefficient has been demonstrated both theoretically and numerically.
How Different Surface Models Affect Absorption Performance
The absorption performances of the rigidly-backed porous absorber and the acoustic curtain with an air layer behind it were evaluated. The porous material was considered as an equivalent fluid with a thickness of 100 mm. The fluid property was modeled using the empirical Miki model with a flow resistivity of 13,900 Pa s/m2. Since the acoustic curtain used is very thin with respect to the wavelength at studied frequencies, the permeable membrane model was used and then was coupled with the air layer. With the permeable membrane model, the transfer impedance of the curtain was calculated with the following equation:
Here,R_{\rm C}andM_{\rm C}represent the flow resistance and the surface density, which were set to 416 Pa s/m and 0.5 kg/m2, respectively. For theoretical study, the TMM was used, and the statistical absorption coefficient was evaluated as the random incidence value. The definition of the statistical absorption coefficient\alpha_{\rm s}is shown below:
The transfer matrix of thin material{\bm T}_{\rm T}is expressed as follows:
1 & Z_{\rm t} \\
0 & 1 \\
\end{bmatrix}
With the transfer matrix above, the specific acoustic impedance of the acoustic curtain with air layer results in the following:
For TMM, the local reaction model can be evaluated by substituting\theta=0.
In the numerical investigation, we calculate the reverberation room absorption coefficient, which is the absorption coefficient measured in the reverberation room. The value of the coefficient depends on the measured room and the sample size. The absorption coefficient was standardized as a measurement procedure as early as ISO:354 and has been widely used in actual room acoustic design.
To efficiently simulate the measurement of the reverberation room absorption coefficient with COMSOL Multiphysics®, the only hard floor with embedded sound absorber was modeled in two dimensions, as shown below.
 Embedded sound absorber model for evaluating the reverberation room absorption coefficient.
Embedded sound absorber model for evaluating the reverberation room absorption coefficient.
The verification study in Ref. 3 showed that this simplified model closely approximated the measurement of reverberation coefficient.
ThePressure Acoustics, Boundary Elementsinterface was used to model the incident pressure field and the rigid floor, and thePressure Acoustics, Frequency Domaininterface was used to model the pressure inside the absorber. ThePoroacousticsfeature was used for the porous material. With theAcoustic FEM–BEM Boundaryfeature, the transfer impedance of the acoustic curtain can be set simultaneously. For local reaction modeling, the absorber domain is disabled, and the corresponding normal incident acoustic impedance is assigned to the surface of the absorber. The evaluation of the reverberation room absorption coefficient is performed in the following steps:
- Evaluate the incidentW_{{\rm i},\theta_n}and the absorbed energyW_{{\rm a},\theta_n}on the absorber surface for a plane wave of incident angle of\theta_n.
- Calculate the ratio of total absorbed energy to the total incident energy with the following equation.
The reverberation room absorption coefficient\alpha_{\rm r}is shown below.
Here,Nis the number of incident angles. In the numerical test, the plane wave incident field was modeled withBackground Pressure Field, andW_{{\rm i},\theta_n}andW_{{\rm a},\theta_n}were defined as follows:
wherep_0is an amplitude of incident pressure, and\bm nand{\bm I}_{\theta_n}are the normal vector and the sound intensity vector of incident angle{\theta_n}on the absorber surface.
The graph below compares the random incidence absorption coefficients of the porous absorber. The difference between the local and extended reactions is small, but can be seen, especially at high frequencies. Thus, as exemplified above, the local reaction model seems to be a good approximation for the porous material with the high flow resistivity and the rigid end.
 The random incidence absorption coefficients of the porous absorber.
The random incidence absorption coefficients of the porous absorber.
On the other hand, the comparison of the random incidence absorption coefficients of the acoustic curtain, shown below, presents the large discrepancy between the local and the extended reaction models. This is due to the strong incident-angle dependency of the air layer. It also corresponds to the conventional rule that the extended reaction modeling is important for the absorbers with air layer.
 The random incidence absorption coefficients of the acoustic curtain.
The random incidence absorption coefficients of the acoustic curtain.
Reverberation Room Absorption Coefficients vs. Statistical Values?
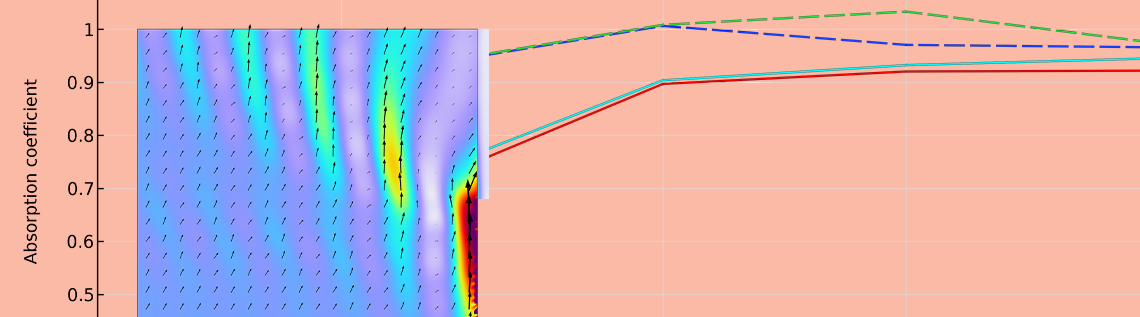
As shown in the absorption coefficient graphs above, regardless of the type of absorbers and absorption boundary models, the reverberation room absorption coefficients are greater than the statistical values and exceed 1 (above perfect absorption). This phenomenon, called “edge effect”, is typical in real measurements and is caused by the energy flow from the rigid floor to the absorber surface. Such a situation is shown against the extended model of the acoustic curtain below for an angle of incidence of 60°at 500 Hz. The energy flow is caused by the sound pressure gradient around the sample edge: The sound pressure near the floor takes a larger value due to the contribution of the reflected sound, while the sound pressure in front of the absorber becomes smaller due to the sound absorption effect. The energy flow occurs around the edge of the sample, and its effect on the sound absorption coefficient can be reduced by increasing the area of the sample. Therefore, the sample size for measuring the reverberation room absorption coefficient is regulated in ISO:354.
 The visualization of the amplitude and arrow of acoustic intensity at 500 Hz for an incident angle of 60°.
The visualization of the amplitude and arrow of acoustic intensity at 500 Hz for an incident angle of 60°.
Conclusion
This blog post presented the theoretical aspect of sound absorption at boundaries and explored how the type of sound-absorbing boundary model affects the sound absorption performance. For room acoustics modeling, theRay Acoustics, Pressure Acoustics, Frequency DomainandPressure Acoustics, Time Explicitinterfaces are well-suited physics interfaces in COMSOL®. TheRay Acousticsinterface is based on geometrical acoustics and cannot accurately capture the behavior of acoustic waves. However, our implementation can capture the behavior with incident-angle dependency of the sound absorption on surfaces, which helps to enhance the accuracy of room acoustics modeling.
The wave-based approaches exactly model the sound absorption characteristics at boundaries. ThePoroacousticsandInterior Impedancefeatures are used to model extended reactivity of the sound-absorbing boundary. ThePressure Acoustics, Frequency Domaininterface can easily deal with these conditions because the method is inherently frequency dependent. On the other hand, the time-domain modeling of the extended reaction boundary conditions is very challenging due to the difficulty of modeling the frequency dependency of the absorption property in the time domain. However, we can use thePoroacousticsfeature in the time domain to model porous absorbers with extended reactivity. The time-domain version of this feature uses an efficient auxiliary differential equation method to account for frequency dependence in porous materials. Thus, you can flexibly choose the sound-absorbing boundary models according to the configuration of the absorbers.
In a future blog post, we will use the time-domainPoroacousticsfeature to explore and discuss how the choice of sound-absorbing boundary types affects the acoustics in the meeting room.
References
- Z. Maekawa, J. H. Rindel and P. Lord. Environmental and Architectural Acoustics. CRC Press, 2010.
- J.F. Allard and N. Atalla. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. Wiley, 2009.
- T. Sakuma, S, Sakamoto and T. Otsuru. Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation. Springer, 2014.




Comments (1)
Said Bouta
January 11, 2025Hello,
Thank you for any information you can provide regarding acoustic absorption. I would like to simulate the sound absorption of a concrete block that contains polyurethane material in its voids. Could you explain to me the method and boundary conditions applied on this model? Additionally, what parameters (e.g., density, Young’s modulus, absorption coefficient, etc.) are critical for achieving accurate results?
Thank you in advance for your guidance!