带标签的博客文章 RF 模块
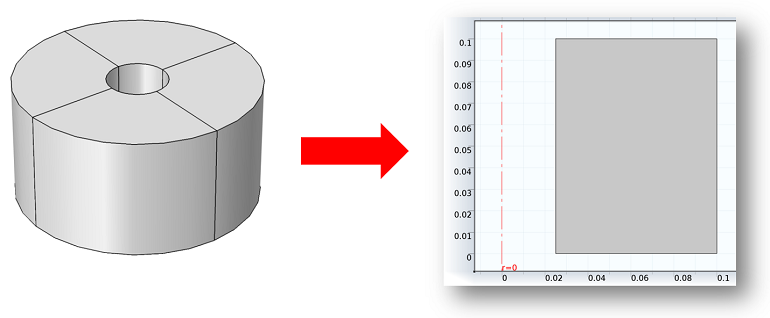
由二维轴对称电磁模型创建可视化三维绘图
今天,我们将介绍在 COMSOL 软件中如何绘制矢量场的三维视图,这些矢量场由 RF 模块和波动光学模块中的电磁波、频域 接口的二维轴对称公式计算获得。 由二维轴对称解生成三维绘图 回想一下,COMSOL 软件中的时谐分析 假设场分量根据 e^{j\omega t} 在时间上振荡,其中 \omega 是角频率。在二维轴对称公式中,电场的角度依赖性由 e^{-j m \phi} 计算,其中 m 是用户指定的整数。由时间和角度的相关性 e^{j(\omega t-m \phi)},可知电场围绕 Z 轴 旋转。我们的目标是由具有这种角度依赖性的二维轴对称解创建三维绘图。 使用二维旋转数据集创建三维绘图 在计算出二维轴对称问题的解之后,COMSOL Multiphysics 会自动生成一个名为“二维旋转”的位于“数据集”节点下的二维数据集,如下图所示。 旋转数据集可用于绘制三维视图。由于我们绘制的是三维绘图,因此将完成一次从 0° 到 360° 的完整旋转。“二维旋转1”的设置如下所示。可以看到,在 “旋转层”下,起始角度被设置为 0,旋转角度被设置为 360。 二维轴对称计算中的平面坐标为 (r,z)。由于角度 \phi 不属于计算域,因此没有被定义。不过,可以通过选中“定义变量”旁的复选框将它添加为三维数据集中的坐标。“二维旋转1”数据集中的角度变量名被设置为“rev1phi”,并可用于下文中的绘图和导出值的表达式中。 如下图所示,考虑一个带矩形截面的轴对称谐振腔。在二维轴对称公式中仅模拟矩形截面。 我们可以使用特征频率研究计算谐振模式。假设我们想绘制 m = 1 模式的场量。下图左侧为在 rz 平面 绘制出的电场大小。我们还可以在将空腔一分为二的表面上绘制电场的大小,这是使用 xy 平面 上的“emw.normE”三维切面图绘制的,平面数被设为 1。右下图中绘制了电场的大小。由于场是围绕 Z 轴 旋转的行波,因此它是轴对称的,这也是因为它遵循 | e^{j(\omega t – m \phi)} | = 1。 绘制电场的径向分量 现在,我们来绘制空腔平面内电场径向分量的实部。具体来说,我们将绘制 t=0 时的 Re { E_r(r,z) \, e^{j(\omega t-m \phi)} },其中 […]
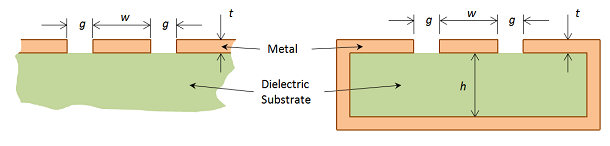
使用 COMSOL 模拟共面波导
共面波导 (CPW) 常用于微波电路中。使用 COMSOL Multiphysics 及其附加产品 RF 模块,您能够轻松地计算设计共面波导时所需的阻抗、场、损耗和其他工作参数。 二维接地共面波导设计 下图为2个典型的共面波导的横截面。如图所示,介电基板的顶部刻蚀有金属层。当基板底部也刻蚀金属层时,称为接地共面波导。底部的金属层通常是经通孔连接至电介质顶部的金属层。虽然这些金属层常常被称为接地,但是金属层中有电流流过,因此表面的电势并不恒定。接下来,我们将重点讨论接地共面波导的示例。 共面波导可以由以下特征参数表征:金属迹线层厚度 t,中心导体宽度 w,中心导体和侧导体之间的间隙 g。如果是接地波导,还包括介电基板厚度 h。 无论进行任何仿真分析,都需要先计算趋肤深度: 以工作频率为 1GHz 的器件中使用的铜为例,其相对磁导率和介电常数为 1,电导率为 6×107S/m,趋肤深度为 2.05µm。由此可知,电场和电流衰减为:,其中 是进入金属的距离。趋肤深度和金属层的厚度将决定需要进行什么分析。如果趋肤深度和迹线厚度相同,则有必要将金属域本身包含在 COMSOL 模型中。另一方面,如果趋肤深度远小于迹线厚度,至少小 10 倍 (), 那么金属层一侧的场不会显著影响另一侧的场。在这种情况下,没有必要对金属层的内部进行建模,可以将它们看作模拟域的边界。 另外,如果金属层的厚度 t 足够小,使得其对结果的影响可以忽略不计,那么我们可以将金属迹线建模为理想电导体 (PEC) 边界条件。例如,下图显示了一个最简单的共面波导模型,该共面波导上方的空气区域可以通过代表金属封装的理想电导体边界条件,或代表没有电流流过的表面的理想磁导体边界条件来截断。 我们可以使用 RF 模块建立和求解此类模型,选择二维模式分析研究类型。计算阻抗 Z=V/I;计算电压 V 沿导体之间的任意一条线获取电场的路径积分,此处标记为 A;计算电流 I 沿任意路径环绕中心导体对磁场进行积分,标记为 B。同轴电缆的阻抗教程模型提供了一个类似的示例,其中详细介绍了如何设置这类模型。 建立三维共面波导模型的 3 种方法 上述二维模型可以快速计算共面波导的阻抗,并可以帮助我们了解横截面中的相对场强。然而,我们通常对一些结构上有变化,需要建立完整三维模型才能求解的设备更感兴趣。这就提出了如何激励三维共面波导模型的问题。我们可以采用多种不同的方法,但首先可以考虑使用理想电导体表面建模的共面波导,其迹线厚度 t,可以忽略不计。 1.为模型添加矩形面 如下图所示,一种方法是向模型中添加几个矩形面,这些矩形表面可以垂直或平行于共面波导平面,代表探针尖端。这些理想电导体表面充当两侧导体之间的桥梁。然后在电桥和中心导体之间的另一个矩形面上应用集总端口激励。该集总端口在相邻的理想电导体表面之间施加电压差(注意:图中箭头的方向是任意的,它们只是为了表明存在沿箭头方向流动的正弦时变电流)。 这种方法非常简单,只需要对模型进行少量修改。要了解使用此方法激励的共面波导模型的示例,请查看 COMSOL 案例库中接地共面波导上的 SMA 连接器模型。 2.通过两个集总端口减少修改 实际上,上述方法需要向模型添加一些额外的结构,因此我们可以考虑一种需要更少修改的方法,如下图所示。通过在中心导体两侧增加 2 个集总端口也可以激励共面波导。 这种方法的唯一困难是它需要手动设置;2 个集总端口功能中的端口号、尺寸以及最重要的是,方向 相同,而且必须设置集总端口的方向,使它们要么都指向中心导体,要么都指向远离中心导体。 相比于第一种方法,这种方法在模型中引入了较少的额外结构,但确实需要两个端口特征,因此必须手动设置并指向正确的方向。 3.模拟两点探针 我们还可以扩展共面波导的布局,以及将理想电导体的侧平面扩展为围绕中心理想电导体的带状结构,然后为集总端口引入一个额外矩形,模拟两点探针,如下所示: 结束语 当然还有其他方法可以激励共面波导,但以上3种方法是最常见的。这 3 种方法的解之间的差异应该很小,但应该注意,所有这些都是为了近似激励,并且集总端口附近的场并不是理想的物理场。这是一种局部效应,远离激励的场和计算的阻抗等量应该更准确。 为了获得最高的保真度,可以对同轴波导的耦合进行具有完整细节的显式建模,如上图所示。有关说明此方法的类似示例,请参阅 Wilkinson 功分器模型。 所有上述方法都可以推广到共面波导金属迹线厚度值很大的情况,或者金属层必须明确包含在模型中而不是通过边界条件近似的情况。其他激励策略当然也是可行的,但这些是最常见的方法。学习了这些方法,您就可以自信地使用 COMSOL Multiphysics 和 RF 模块进行共面波导的建模和设计。
