
特征频率分析是数值仿真工具包中不可或缺的一部分。线性系统的特征模态通常具有明显的定性特征,并在如频率等参数范围内以不同的方式演变。我们经常被问到,是否有办法对这些随参数范围变化的特征模态解集进行追踪和分类。这篇博客,我们将演示如何使用 COMSOL Multiphysics®软件中的模态重叠积分法来实现这一目标。
特征模态和重叠积分
小测验:为下一代通信系统设计光缆,优化桥梁设计以尽量减少不必要的机械共振和优化客厅的声学布局,这三者有什么共同之处?
对于上述每一个场景,我们都必须充分了解系统的特征模态。特征模态及其相关特征值(也称为固有频率)描述了线性系统对外部激励的响应方式,因此在设计中起着至关重要的作用。在一些应用中,例如射频通信腔滤波器或扬声器驱动器,我们希望能最大程度地耦合一个或多个特征模态,而在其他应用中,这些共振模态的耦合可能会导致灾难性后果,如桥梁坍塌。
当在参数扫描过程中调整系统参数,如工作频率或几何尺寸时,特征模态和频率自然会发生变化。然而,这些模态通常会保持定性相似性。让我们来看一个简单的示例,像鼓或克拉尼板振动表面一样的二维椭圆形薄膜的波动方程。
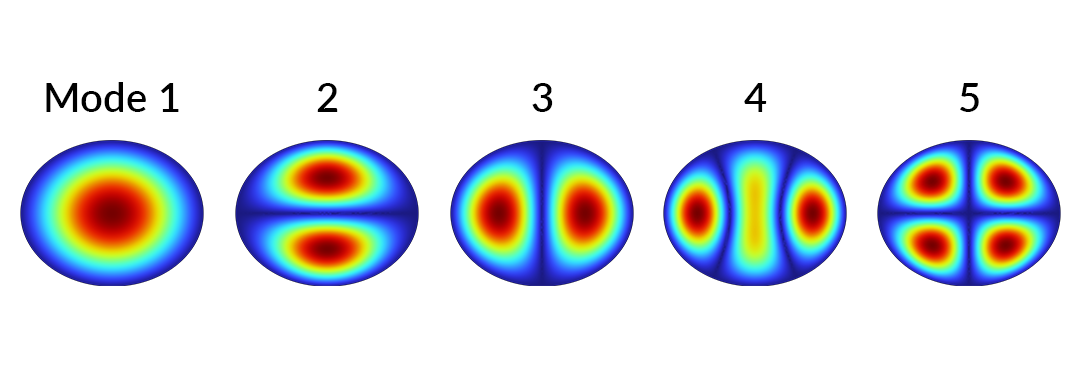
具有固定边界的椭圆形薄膜的二维波动方程的前 5 个特征模态解。
特征频率研究显示了前 5 个特征模态,其位移大小如上图所示。现在,假设我们要对椭圆域的垂直高度进行参数扫描。
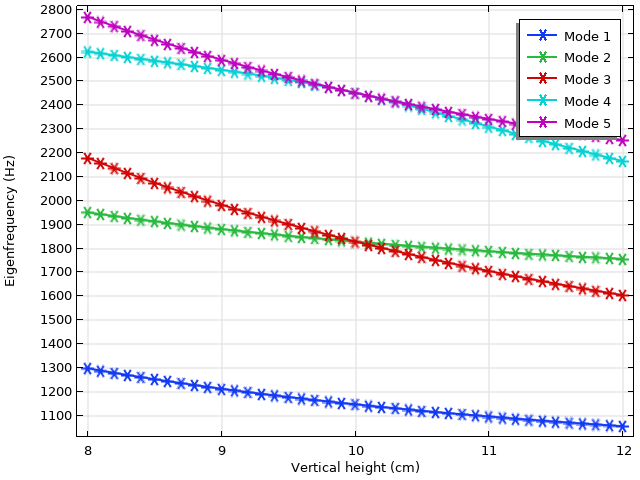
图中显示了前 5 个模态的特征频率与椭圆域垂直高度的关系。请注意,在高度为 10 cm 时,模态 2 和模态 3 ,模态 4 和模态 5 之间的简并,而此时椭圆域是圆形的。
前 5 个模态的特征频率如上图所示。请注意,当垂直高度为 10 cm 时,模型域是圆形的。这导致模态 2 和 3 之间,模态 4 和 5 之间的简并。事实上,过了简并点,模态 2 和 3 就会在特征值图中互换阶次。这种模态交叉行为在许多特征频率研究中都很常见。当这些模态的阶次发生变化时,如何在特征值图中追踪它们呢?要回答这个问题,让我们仔细观察其中的一个模态。
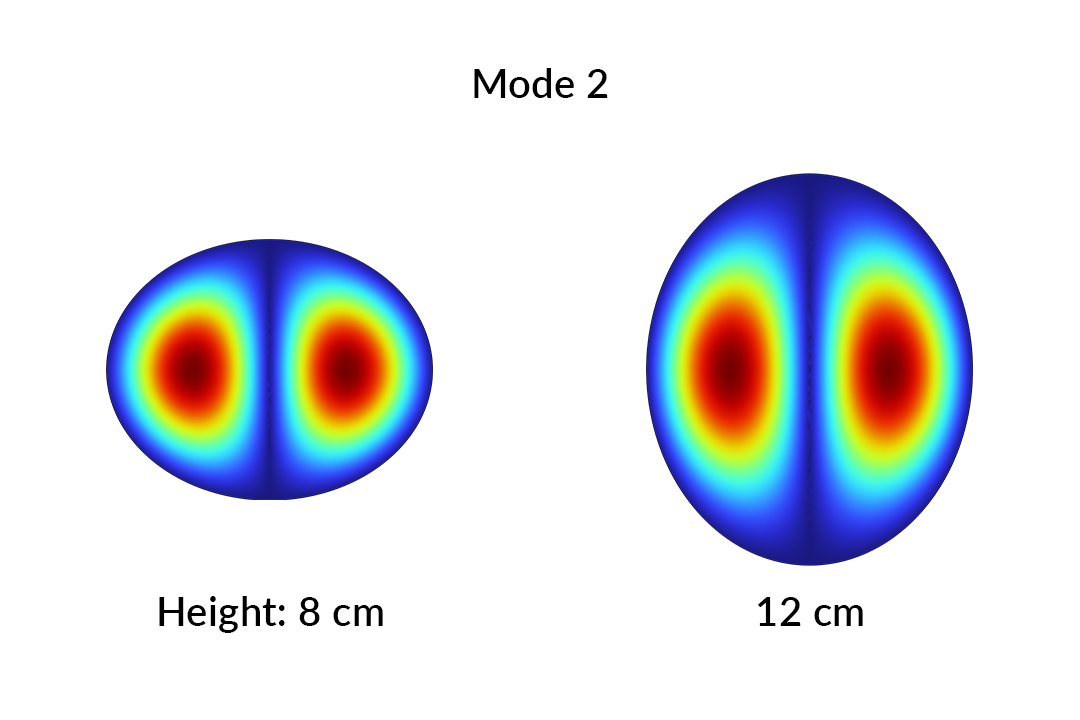
参数范围两个端点处的模态 2。
高度为 8 cm 和高度为 12 cm 时的模态 2 如上图所示。通过肉眼就可以明显观察到这两个模态的相似性。我们可以用模态重叠积分来量化这种相似性:
变量u_i和u_j代表两个任意的特征模态解。这个方程的关键部分在于分子:在两种模态之间进行内积。分母将重叠度M的值归一化,使其介于 0 和 1 之间。
一个模态与其自身的重叠度为 0,因为它们是相互正交的。对于参数值不同的模态,只要模态在性质上相似,M 接近 1。例如,上述两个模态的重叠度 M = 0.95,证实了我们的直观识别。两个不相似的模态的重叠度接近 0。
利用这一度量标准,我们可以通过对重叠值施加一定的阈值,来建立模态匹配方案。这可用于色散图中过滤或分组模态,甚至在模型方法的帮助下自动生成模态轮廓动画。接下来,让我们看看如何将这一策略应用到多个不同的物理学科。
示例 1:光学各向异性波导
在上一篇关于如何模拟光学各向异性介质的博客中,我们研究了光学各向异性波导的横向模式。这些模式可以按照电场的主要方向以及横向平面上振幅最大值的数量进行分组。E^x_{ij}模式的一些示例如下图所示。
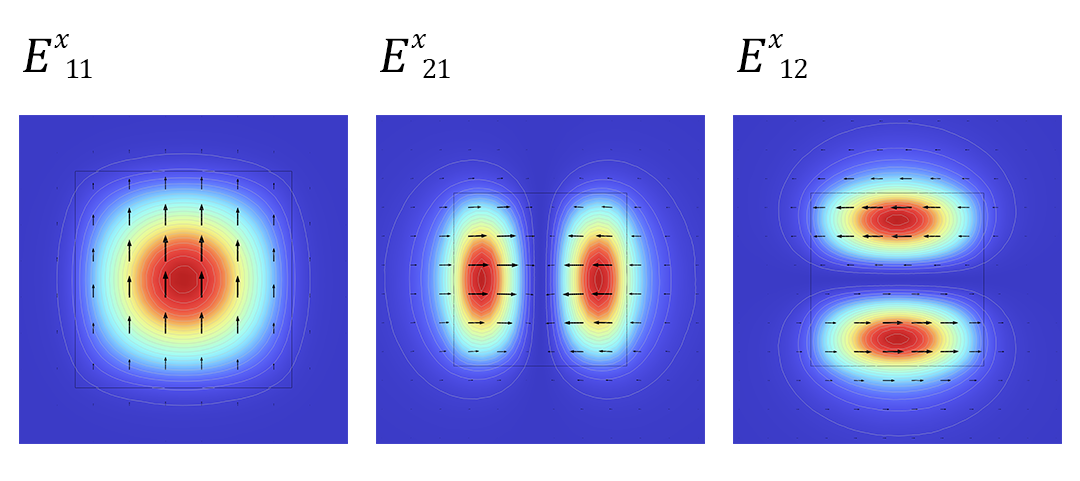
光学各向异性波导中前 3 个E^x_{ij}特征模式。
由于波导的主要目标是控制光流,因此了解这些传播模式的行为至关重要。在每个频率下,每个模式都有一个相关的有效折射率,该折射率决定了它们的传播速度、有效波长以及衰减程度(如果模型中存在损耗)。我们使用色散图来绘制有效折射率随频率变化的曲线。
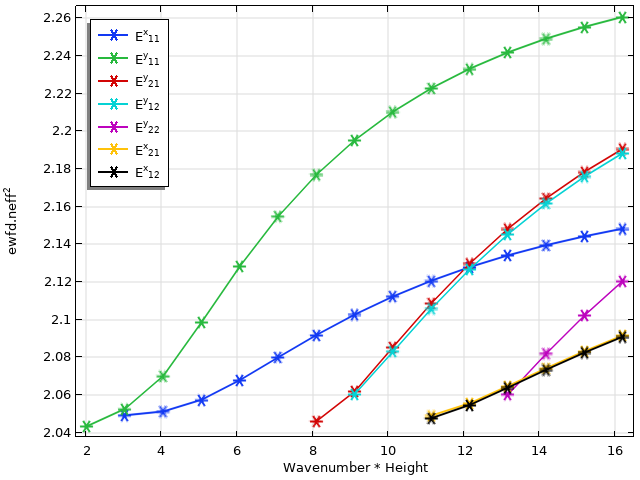
波导的色散图如上所示。由于存在大量的模式交叉,因此有必要对特征模式进行分类,以便正确标记。
在模式分析研究的原始输出中,没有以任何有意义的方式有效折射率进行分组或排序,因为求解器没有这些模式的先验知识。我们采用重叠积分计算方法,按模态轮廓对这些特征值进行分类。现在,由于每个有效指数值都与特定的E^x_{ij}或E^y_{ij}模式相关联,因此我们可以轻松地使用滤波器和绘图选项在绘图图例中为每个模式着色和标注。请注意,这种方法能够正确解析多模式交叉以及特征值非常接近的模式,例如E^{x,y}_{12}和E^{x,y}_{21}模式的交叉。
示例 2:旋转叶片的特征频率
深入理解风力涡轮机叶片或电动汽车电机等旋转部件的共振模态,对于稳定性分析或最大限度减少噪声和振动等应用至关重要。我们来看 COMSOL应用库中的一个基本示例:旋转叶片的基本特征频率模型。
当矩形叶片以越来越大的角速度旋转时,预计会出现两种主要的竞争现象:应力刚化和旋转软化。前者由于离心效应产生的静态应力场使叶片变硬,从而对固有频率产生向上的影响。后者则由于运动的径向放大而使叶片软化,导致对固有频率的向下影响。这些效应的平衡在坎贝尔图中得到了最好的体现,即固有频率与旋转角速度的关系图。
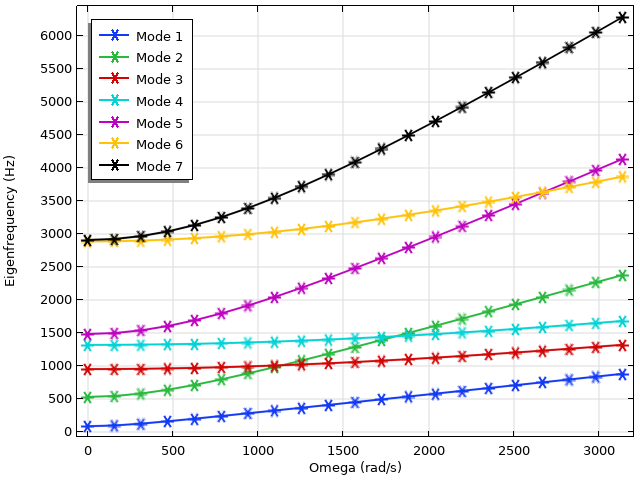
旋转叶片的坎贝尔曲线图。请注意,模态 2 和 5 的特征频率明显增加。
上图是前 7 个特征模态的坎贝尔曲线图。总体而言,我们观察到固有频率呈上升趋势,这表明应力刚化起了很大作用。这在模态 2 和 5 中更为明显,在所研究的参数范围内,这两个模态的特征值急剧上升,并超过了其他模态的特征值。前 6 个模态的位移和应力如下图所示。
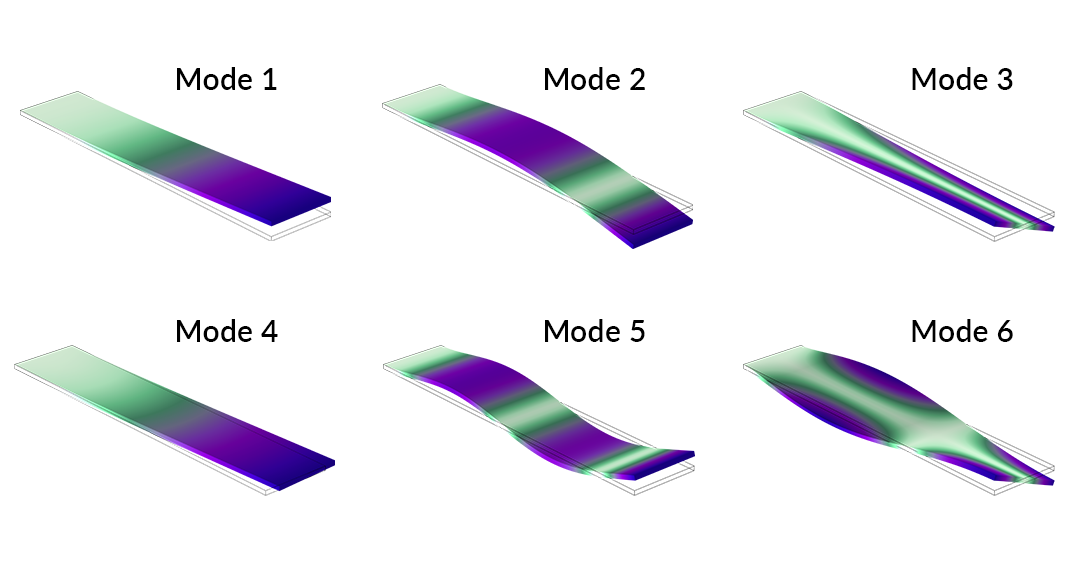
旋转叶片的前 6 个特征模态。
在更复杂的系统中,坎贝尔图中的固有频率可能更多,既有上升趋势,也有下降趋势。了解这些趋势并将其可视化,对于确定如临界转速等至关重要。通过模态重叠积分,可以轻松地对这些模态集的行为进行分类和追踪。
示例 3:带弹性壁的消声器特征模式
多物理场仿真在内燃机消声器的设计中发挥重要作用。除了模拟空气中的压力波外,还必须考虑空气与消声器外壳之间的相互作用,从而可以更加准确地模拟整个频率范围内的传输曲线。
声-结构相互作用的其中一种效应是引入更多的共振模式,这一点可以通过两个相关的示例来说明:消声器中的特征模式和带弹性壁消声器中的特征模式。我们来详细探讨后一个模型。在一定频率范围内对消声器横截面进行模式分析,以确定模式轮廓及其相应的截止频率。
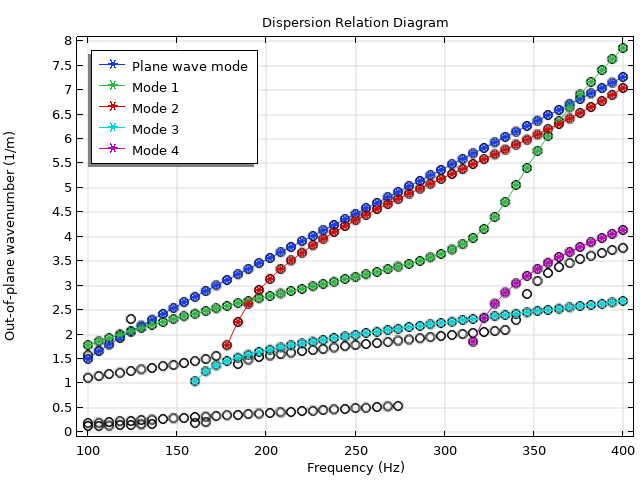
带弹性壁的消声器色散图。除平面波模式(蓝色)外,由于空气与消声器壁之间的声-结构相互作用,还存在许多其他模式集。使用模式重叠积分法跟踪了其中的一个子集。
上面的色散图绘制了部分模式及其传播常数与频率的关系。显然,数据集中的趋势很可能与不同的模式系列相对应。例如,平面波模式形成了一条贯穿整个频率范围的对角直线。通过应用重叠积分,我们可以确认平面波模式的预期行为,并追踪整个频率范围内的其他几个模式。模式轮廓图如下所示。
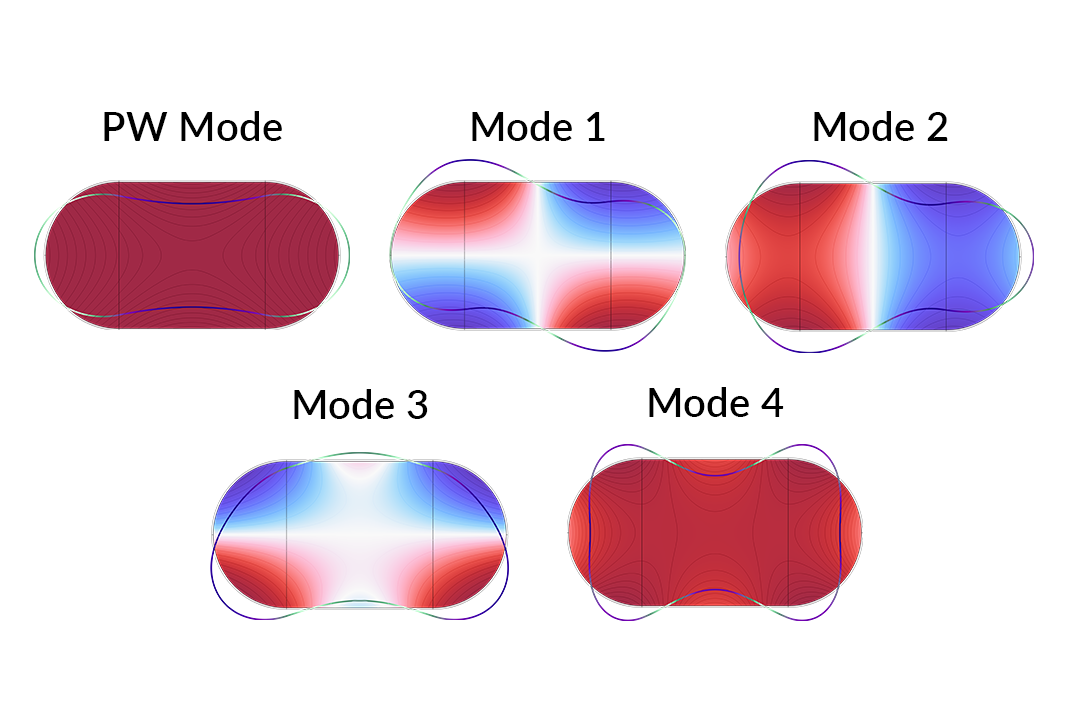
上图显示了带弹性壁的消声器中的部分模式轮廓。
借助模型方法,我们甚至可以自动生成整个频率范围内的模式演变动画。
在模型方法的帮助下,在整个参数范围内对模式 3 的演变进行追踪并用动画演示。
上面的动画演示了模式 3 如何从接近其截止点的 160 Hz 急剧变化到研究的上限 400 Hz,过程中还跨越了其他几个特征模式。在模态重叠积分的帮助下,追踪单个模式集的演变变得更加容易。
下一步
在这篇博客中,我们演示了如何使用模态重叠积分方法在特征频率研究中追踪和分类模态。请点击下面的按钮进入 COMSOL 学习中心,开始学习相关内容:
此外,这篇博客中讨论的模型可在 COMSOL 案例库中下载:



评论 (1)
Zeyu Wu
2024-09-01如何在comsol中定义不同的阶特征频率的物理量的内积呢?