
在模拟计算量非常大的几何结构的时,我们可以利用循环对称来减少内存的使用,从而节省计算时间。相较于轴对称几何结构,对旋转对称几何结构的处理可能更复杂。借助COMSOL 软件附加的结构力学模块,我们可以通过简单地求解叶轮模型的一个部分来求解完整的模型,并且仍能获得准确的结果。
循环对称结构的流体-结构振动分析
在分析涡轮机和压缩机时,了解系统内部的振动十分重要。在涡轮机械中,由流体流动载荷引起的叶片振动最终会导致结构疲劳。因此,对这类几何结构进行特征频率分析非常重要。这种结构本身具有旋转对称性,能够被分解为重复的部分。由此可见,循环对称可以减少计算需求。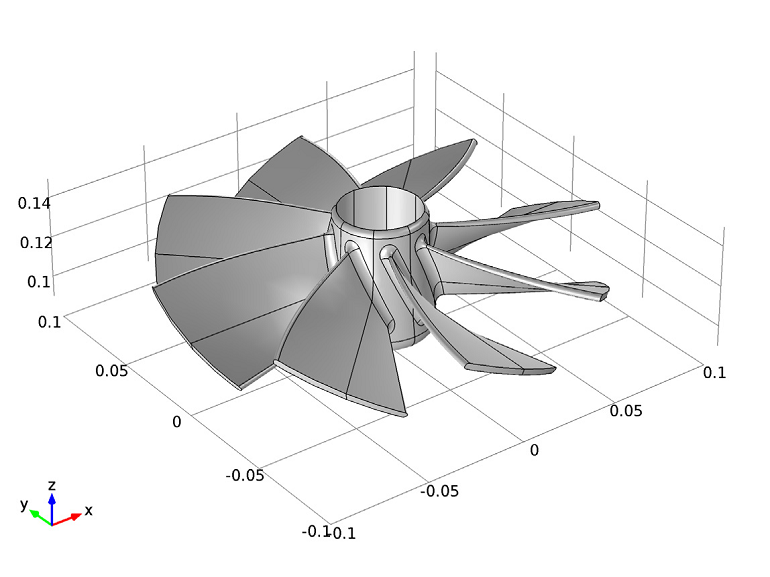
叶轮的几何形状。
模型简介
以 COMSOL 案例库中的案例教程叶轮振动模型为例来说明。该模型将一部分几何结构的分析结果与完整叶轮几何结构的分析结果进行了比较。COMSOL 软件固体力学接口的周期性条件特征内置了预定义功能,可以设置循环对称条件。在该模型中,叶轮的几何形状被分为 8 个相同的部分,如下图所示。
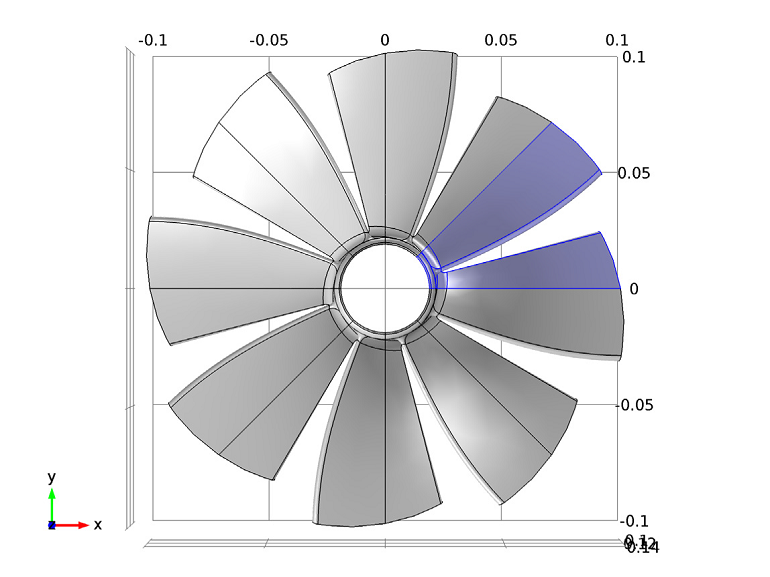
该接口使用Floquet 理论将周期性系统转化为常见的线性系统。在对称扇区的两侧使用 Floquet 周期条件,以防止周期性消失。
模型设置
使用 8 部分 θ=π/4 的扇区来表征叶轮。叶轮安装在一个轴上,轴设置为固定约束并忽略轴的旋转可能产生的影响。现在,我们可以进行特征频率分析研究。利用 ϕ=mθ 的周期角分析特征模态的循环对称,对一个对称扇区进行分析。
在这个方程中,模数m在 0 到 N/2 之间变化,其中 N 是截面总数,所以 θ=2π/N。通过对循环对称参数的所需值进行扫描,准确获得完整模型的所有特征频率。
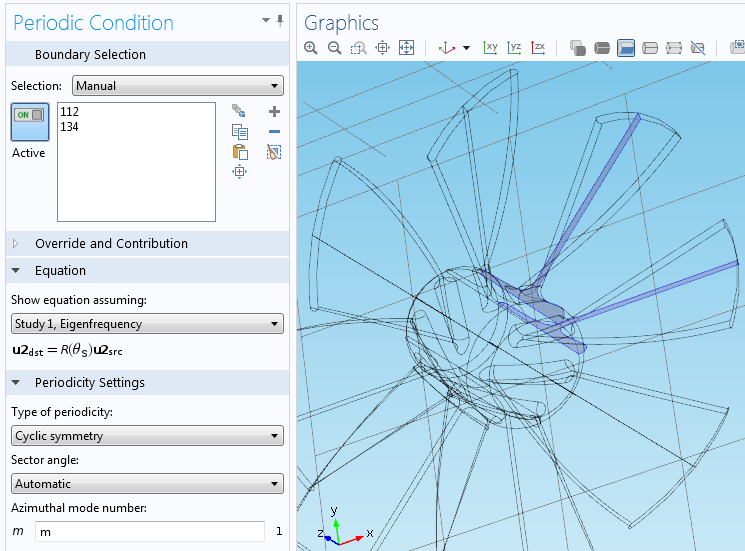
循环对称周期性条件设置窗口。
实际上,当需要减少周期性结构的模型尺寸时,还可以使用其他几种类型的周期性。
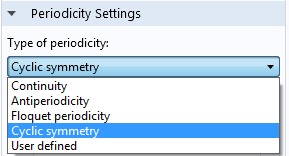
不同类型的周期性条件。
频率响应分析结果一致
我们也可以对周期性部分以及完整叶轮的几何结构进行频率响应分析。通过计算一个扇区的频率响应,然后将结果扩展至完整的几何结构并进行可视化。借助 COMSOL 软件的结果节点下预定义的派生数据集三维扇区,可以实现此操作。以下是频率响应分析的结果:
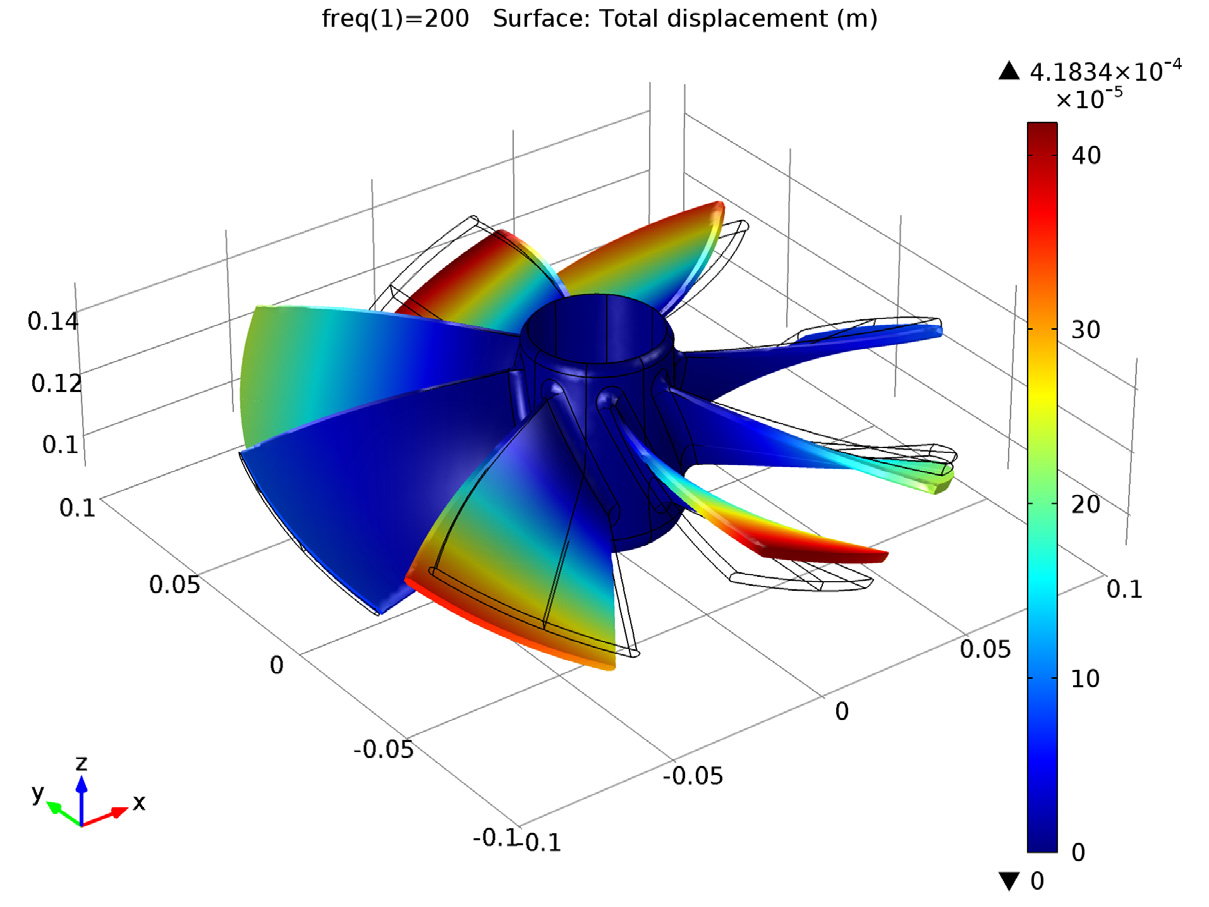
仅对周期性部分计算频率响应,然后将结果扩展到完整的几何结构并进行可视化。
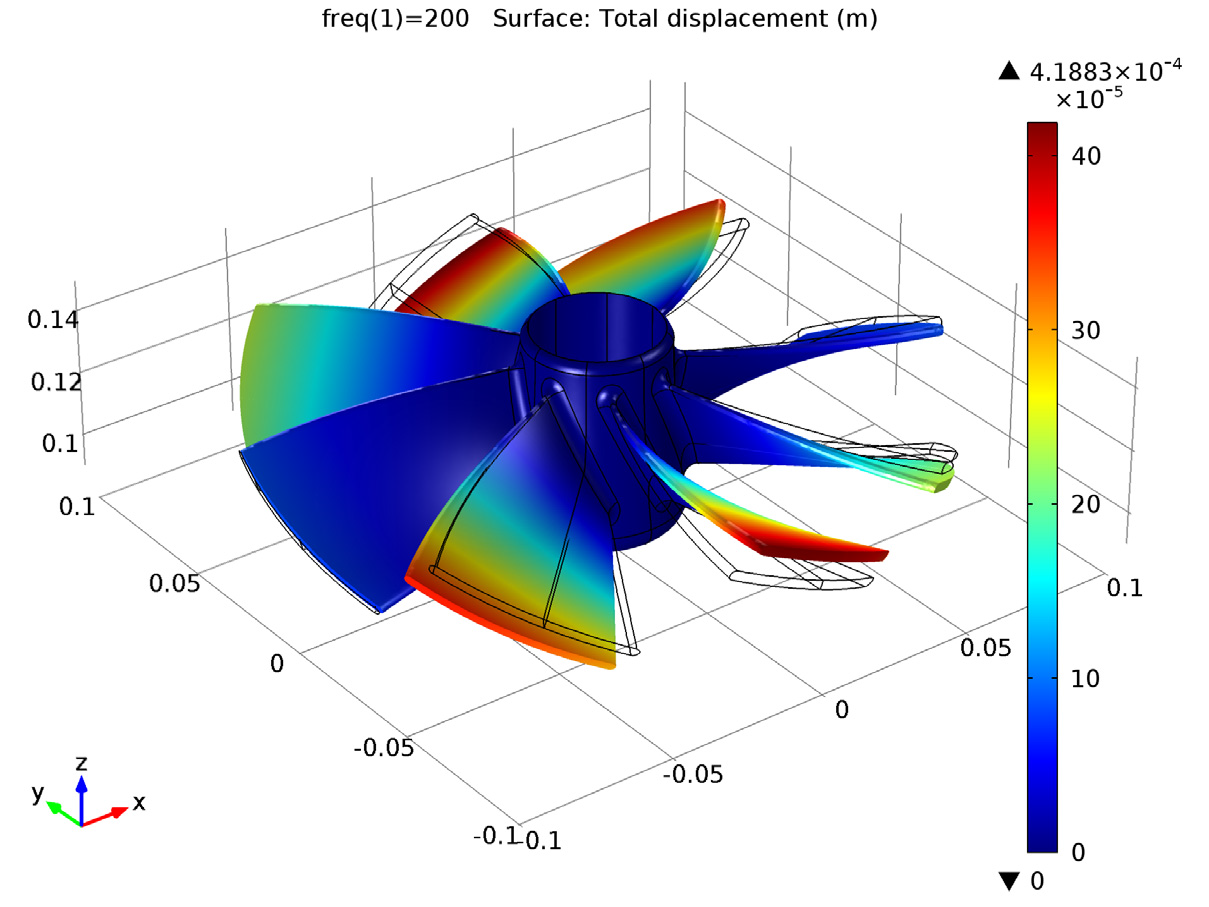
计算完整的几何结构获得的频率响应。
可以看到,两种计算结果具有很好的一致性,这表明使用循环对称条件减少几何尺寸并不会影响结果的准确性。
扩展阅读
- 模型下载:叶轮振动
- 知识库文章:在 COMSOL Multiphysics 中使用对称性减小模型尺寸



评论 (2)
Dunhui Yao
2024-07-17请问模数 m 在 0 和 N/2 中随意取一个值就可以吗?有没有什么取值的依据?
Yuqing Ge
2024-08-02 COMSOL 员工为了使对称模型能计算出所有模态,m应该取完0到N/2中的所有值。