您是否曾经遇到过想要使用一些试验数据作为载荷或边界条件的情况?如果这些数据随空间或时间变化,并且是有噪声的,那么你可能需要非常精细的网格,或者求解器可能需要非常短的时间步进。实际上,我们通常不希望或不需要这样做。一种可能的解决方案是对输入数据进行过滤以使其更加平滑。接下来,让我们了解更多详细操作。
用基于方程的建模方法过滤噪声数据
首先,我们假设一些样本输入数据,如下图所示。现在,我们先不考虑数据代表什么,并假设横轴可以代表空间或时间。我们可以观察到,该数据有明显的噪声,以及明显的趋势。在模型中使用这些数据之前,我们想减少这些噪声。
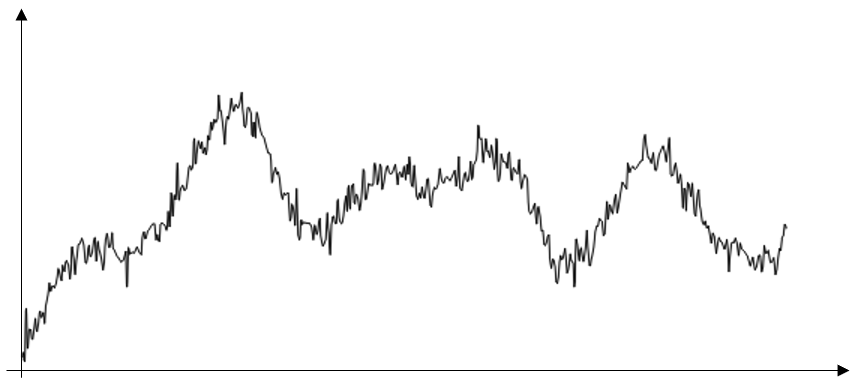
具有明显噪声的数据样本。
在这里,我们可以使用一个所谓的亥姆霍兹滤波器(Helmholtz filter)。这种类型的滤波器是最近被提出并被证明在拓扑优化领域非常有用。其实这个功能是 COMSOL优化模块的内置功能,但也可以手动实现,以下就是我们将演示的内容。
亥姆霍兹滤波器可以方便地求解偏微分控制方程:
式中,D是输入数据,u是过滤后的数据。
方程中有一个参数R,我们将其称为过滤器半径。
除了控制方程外,我们还需要边界条件。因为我们将从齐次诺依曼条件(homogeneous Neumann condition)入手,即边界处的场梯度为零。为了求解该方程以及这个边界条件,我们将在一维组件中的系数形式偏微分方程接口中使用基于方程的建模方法。
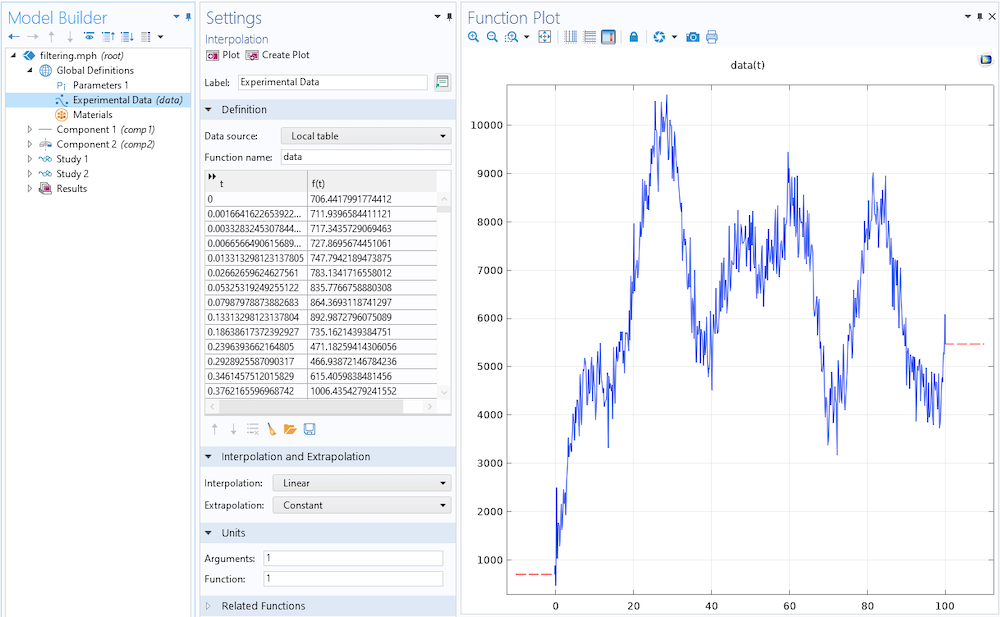
首先,我们将试验数据读入插值表格特征,如下面的屏幕截图所示。需要注意的是,外推被设置为常数。我们很快就会看到,由于亥姆霍兹滤波器中的边界条件,我们需要一些我们关注的空间或时间范围之外的数据作为缓冲区。
接下来,我们将 一维组件引入我们的模型并将单位制设置为无。
然后,在几何中创建一个线段间隔特征,如下面的屏幕截图所示。需要注意的是,在我们关注的数据范围两端的附加区域。
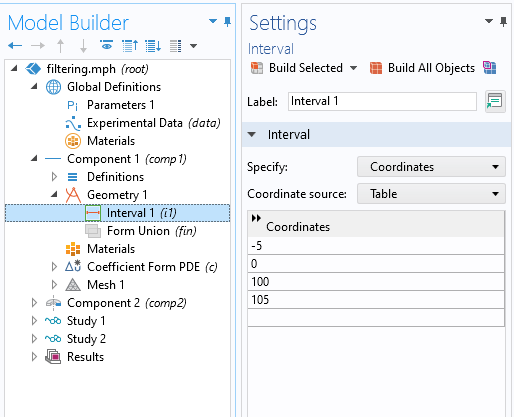
定义应用过滤器的域。
现在,针对单个未知数u,我们将系数形式偏微分方程接口引入到组件中,如下面的屏幕截图所示。我们将保持离散化为默认的二次拉格朗日。然后,保持所有数据无量纲。
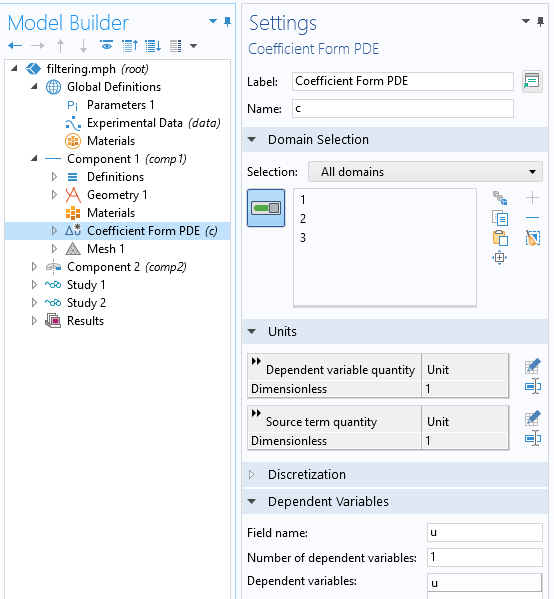
在系数形式偏微分方程特征的设置中,定义如下所示的设置。扩散系数被设置为全局参数FilterSize的平方,吸收系数为1。源是我们的试验数据,而所有其他项均设置为零。
默认的边界条件零通量是所需的齐次诺依曼条件,我们将在计算域的两端将过滤后数据的导数固定为零。这为过滤器引入了末端效应,这就是我们向几何和数据引入额外填充区域的原因。
我们也可以使用狄利克雷边界条件,将在边界处固定u的值。我们还需要手动将网格大小设置为小于试验数据的分辨率。
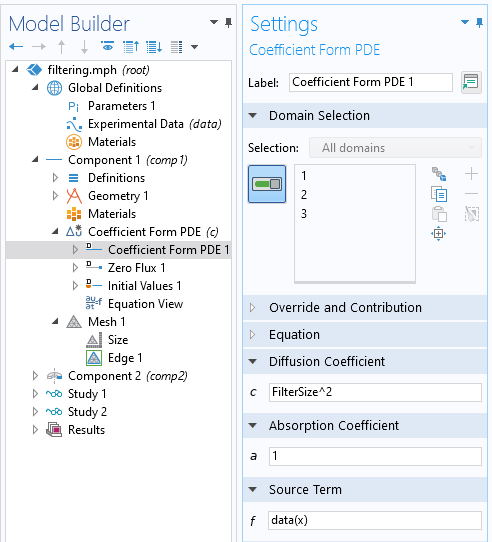
使用基于方程的建模来定义亥姆霍兹滤波器方程。
对模型数据使用亥姆霍兹滤波器方程
现在,我们可以求解不同过滤尺寸的过滤器并比较结果。正如我们在下面看到的,非常小的过滤器尺寸几乎没有影响。过大的过滤器尺寸会导致过于平滑,随着过滤器半径变大,过滤后的数据接近原始数据的平均值。
认识到亥姆霍兹滤波器的这个关键特性很重要:只要使用齐次诺伊曼边界条件,它就能实现能量守恒。这意味着原始数据和过滤后的数据在整个计算域上的积分将是相同的。
请注意,在两端没有缓冲区的子域上,这并不完全正确。还需要注意的是,狄利克雷边界条件不能实现能量守恒,因此应谨慎使用。

使用不同过滤半径的过滤数据示例。
现在我们已经过滤了数据,接下来看看如何在模型中使用它们。假设一个二维轴对称材料的瞬态加热,过滤后的数据将代表暴露表面上施加的热负荷。由于我们的热模型将位于模型的不同组件中,因此需要引入一种方法将我们的数据从一维组件移动到时间维度,以便在二维轴对称组件中使用。这可以通过广义拉伸算子来实现。在这里,我们将t的表达式定义为一个目标。这项功能会将来自一维组件的数据映射或拉伸到时间轴上,并使其在整个模型中均可用。
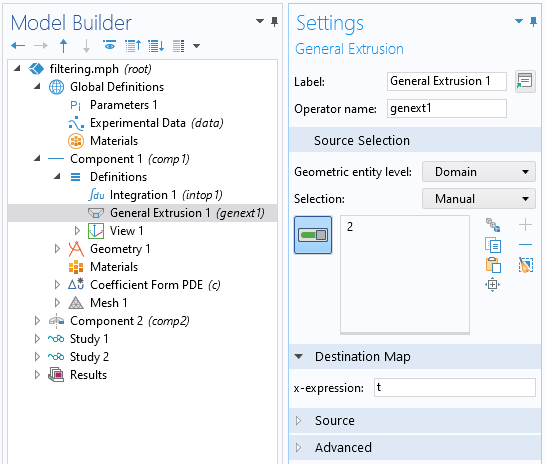
屏幕截图显示了广义拉伸算子的设置。
在二维轴对称组件的热模型中,我们可以施加一个热源,如下面的屏幕截图所示,其中热负荷为comp1.genext1(u)[W/m^2]。请注意,我们为此添加了单位,因为u是无量纲的。
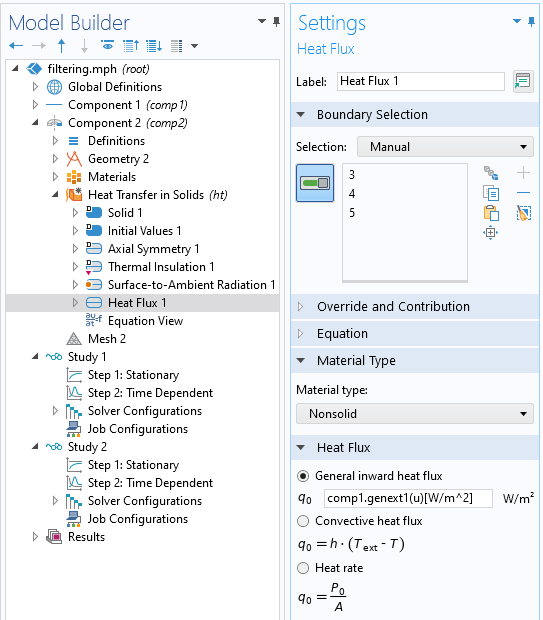
将组件1 中定义的过滤数据调用到组件2 中的热模型。
我们可以将研究分为两个步骤。第一个步骤是一个稳态步骤,求解过滤方程;第二步是一个瞬态步骤,求解热问题。我们将求解更严格的相对容差1e-4,并以求解器采用的所有时间步进输出结果,如COMSOL 知识库的列表中所述。
顺便说一句,还需要注意的是,如果数据在没有噪声的情况下具有明显、剧烈的幅度变化,则应改用事件接口告知求解器。
求解不同的过滤半径值,并绘制域内峰值温度随时间的变化图,我们可以看到过滤对传热问题求解的影响。在这种情况下,随着时间的推移,对峰值温度的影响很小。
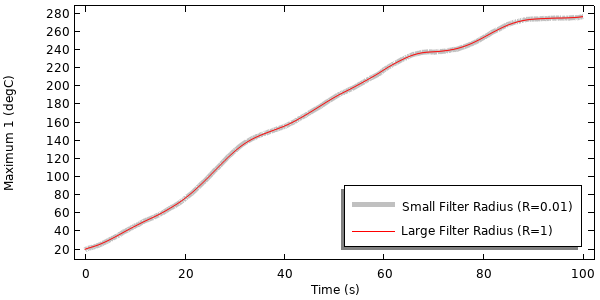
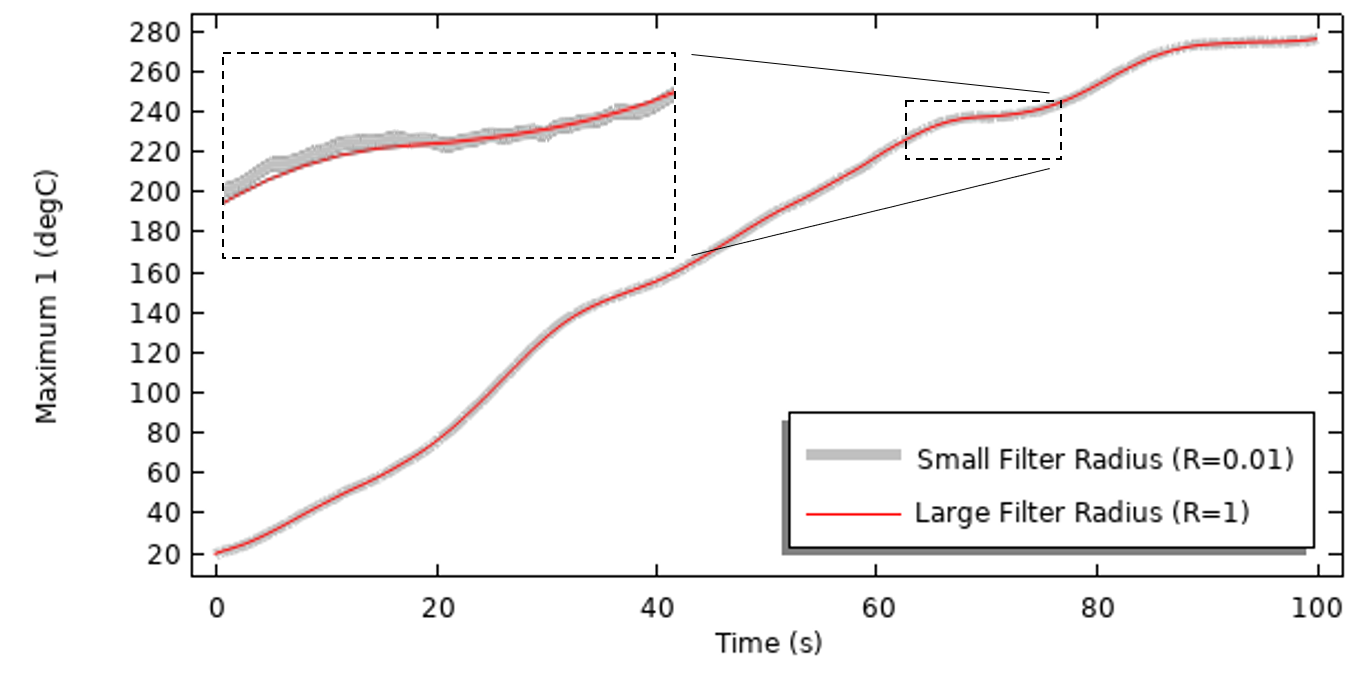
热模型结果,使用了不同的过滤方式来求解瞬态热载荷。
这里最大的差异在于求解时间。求解没有过滤的模型总共需要大约 700 个自适应时间步进,而以中等滤波器尺寸求解模型需要大约 130 个时间步进,求解时间减少了五倍以上!
结论性思考
在今天的博文中,我们展示了如何使用附加组件和方程对输入模型的数据使用亥姆霍兹过滤器进行过滤。我们不仅可以对 1D 数据执行此操作,还可以对 2D 或 3D 数据执行此操作,并且可以对任意几何形状和任意密度的输入数据进行处理。特别是在 2D 和 3D 中,该方法将优于大多数其他过滤技术,因为它利用了有限元基函数的局部紧凑支撑性,并允许非均匀空间网格离散化。这就得到了可以高效求解的稀疏线性矩阵。
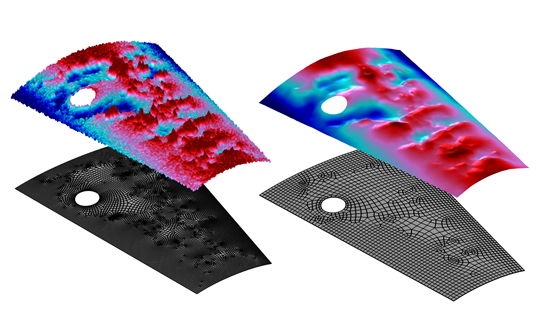
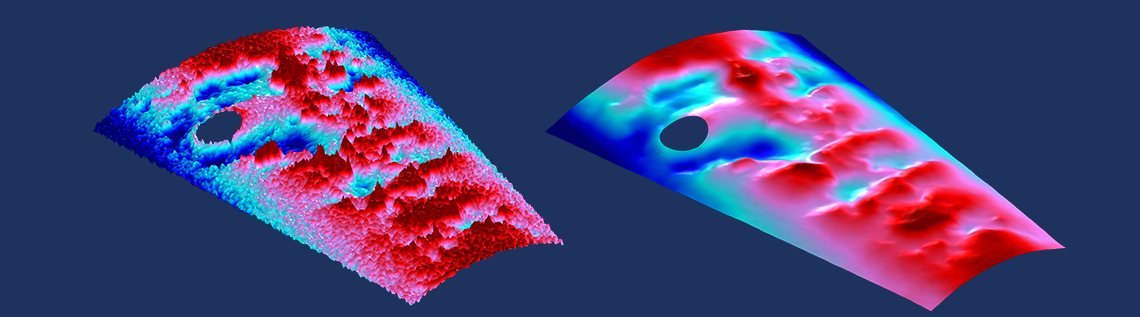
通过亥姆霍兹过滤器在任意表面上进行空间过滤。过滤后的数据用较粗的网格就可以很好地描述。
上图中的示例很好地说明了 2D 平滑处理,即在一个任意表面上未过滤和过滤后的场分布。请注意,对数据进行过滤将允许使用此数据的模型在相对较粗的网格上求解,这为我们带来了额外的计算优势。事实证明,我们甚至可以使用这个亥姆霍兹过滤器来设计一个可以很好地满足不同的输入数据的网格,这将在今后继续讨论,欢迎继续关注我们的博客文章!
自己尝试
与点击下方按钮,可以下载与这些方法相关的文件,尝试自己动手建模:



评论 (0)