
在建立多物理场模型的过程中,我们经常会遇到这样的情况:一个物理场的解是周期性,或者非常接近周期性的,而其他感兴趣的物理场的解是非周期性的。如果我们提前知道这一点,就有可能利用这种周期性来减少计算。这篇博客,我们将演示如何利用 COMSOL Multiphysics 中的广义拉伸组件耦合来实现这一目标。
在微流体设备的多物理场仿真中利用周期性
首先我们来了解一下微流体设备,如下图所示。这类设备中具有很多微小的通道,其中充满了携带不同化学物质的流体。设计这些设备的一个共同目标就是要在一个小表面区域内实现最佳混合,因此通常会被设计为蛇形通道。

一个典型的微流体设备。图片源自 IX-factory STK 。在 CC BY-SA 3.0 下获得许可,通过Wikimedia Commons共享。
下图是微流体设备的示意图,包括两个流体入口,两种流体中的溶剂(水)相同但溶质不同。在出口处,我们希望这些物质能够充分混合。为了模拟这种情况,需要求解流动的纳维-斯托克斯方程。计算出的流场可以作为控制物质浓度的对流-扩散方程的输入。COMSOL 案例下载页面中的微混合器教程就是这种模型的一个示例。
如果需要的话,我们可以对上图所示的整个装置进行建模。但是,如果我们忽略入口和出口附近的结构,就可以合理地假设通道弯曲处的流动在基本单元之间是相同的。因此,可以通过只求解一个单元内的流体流动,并在对流扩散问题的整个建模域中对该流动解进行建模,从而大大简化模型。
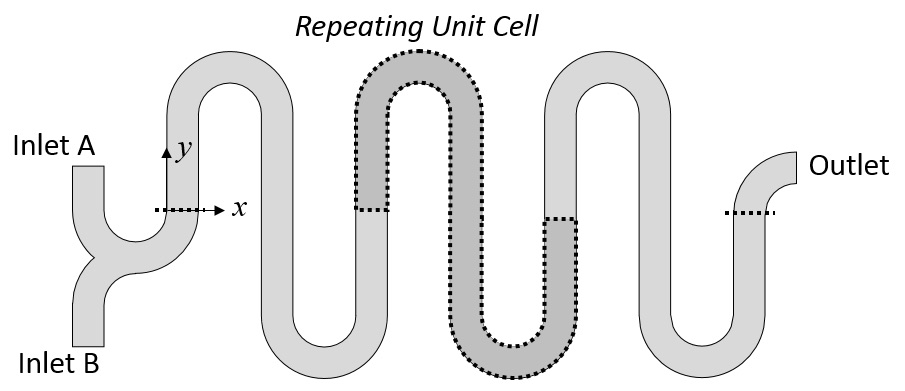
微混合器的示意图,描述了重复的单元以及入口和出口区域。
对于这样一个基本单元模型,将通道的壁设置为壁,无滑移条件。使用周期性流动条件设置速度,以使入口和出口边界处的速度是相同的,这样我们就能指定基本单元上的压降。使用单个点上的压力约束来测量固定压力场。本例中的流体是水,在室温和压力下定义其属性。绘制这个基本单元的流动解,如下图所示。
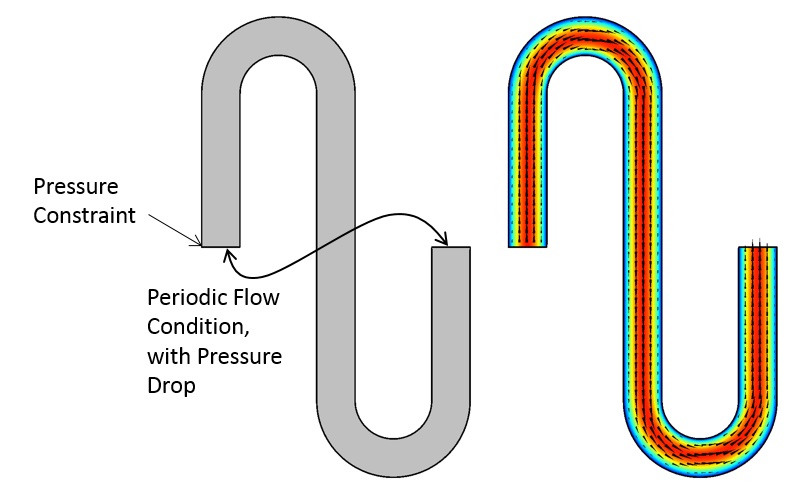
周期性的建模域和流体流动的解。
现在我们得到基本单元的解,就可以使用广义拉伸组件耦合,将解从这个基本单元映射到重复的域上,从而能够定义整个蛇形截面上的流场。
使用广义拉伸组件耦合模仿和重复使用解
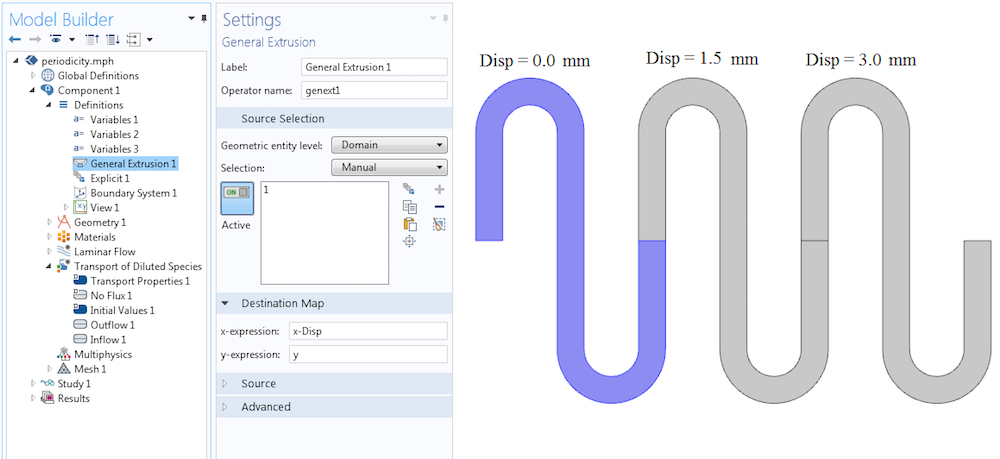
COMSOL 软件模型树中的组件 > 定义 > 组件耦合提供了广义拉伸功能。该功能的设置如下图所示。为了将解从一个域映射到其他域,这些域沿x 轴偏移了一个已知的位移,目标映射使用表达式“x-Disp “作为x表达式。因此,原域中的每一个点都会沿着正x方向被指定的位移所映射。由于在y方向上没有位移,y 表达式被设置为默认的“y”。
如下图所示,变量Disp是在三个域中的每一个域中单独定义的。因此,只需要一个算子就可以将速度场映射到所有域中。在原域内,使用的是零位移。
定义了广义拉伸算子后,我们就可以在整个模型中使用它。在这个例子中,该算子通过稀物质传递接口定义速度场(如下图所示)。速度场由u和v给出,分别是x方向和y方向的流体速度。现在这个速度场的分量已经通过广义拉伸算子genext1(u)和genext1(v),在所有的重复域中分别被定义。
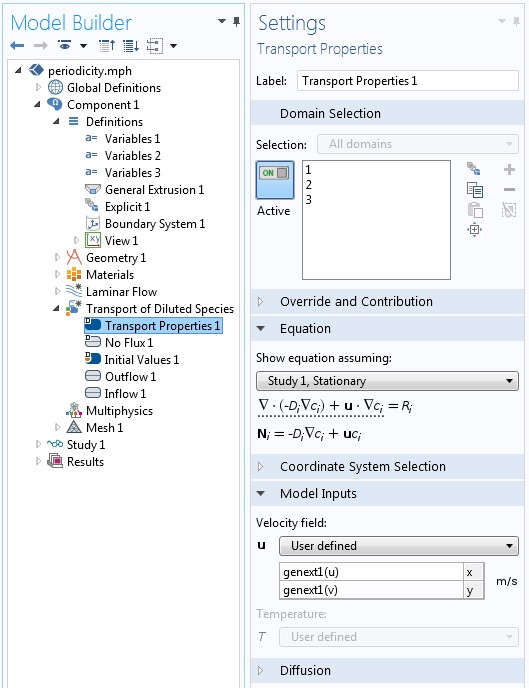
广义拉伸算子用于定义所有周期域的速度场。
现在,整个建模域的速度场已经确定,通过流入边界条件确定入口处的物质浓度。在入口边界上施加一个变化的物质浓度。在另一端施加一个出口边界条件。
虽然严格来说没有必要这样做,但是网格会从一个域中复制到其他所有域中,用于求解流体流动。复制域网格功能可以精确地复制网格,从而避免网格之间流动解的任何插值。
该模型将分两步进行求解,首先求解层流物理场接口,然后求解稀物质传递接口。这样做是合理的,因为它假定流场与物质浓度无关。浓度和映射的速度场的分析结果,如下图所示。

求解了所有重复域中的物质浓度(用颜色表示)。在一个域中求解了箭头所示的周期性速度场,并映射到其他域中。
结束语
本文,我们讨论了如何使用广义拉伸组件耦合来设置周期性解的线性阵列,作为多物理场分析的一部分。对于圆形周期性,必须在目标映射中使用旋转矩阵,而不是线性偏移。在之前的博客中,我们详细介绍了定义这种旋转矩阵的例子。
文中应用的方法适用于其它任意物理场需要利用空间重复解的情况。在您的多物理场仿真中,会在哪里使用呢?



评论 (0)