使用广义拉伸算子建立旋转模型

模拟暴露在载荷下的旋转物体是经常会遇到的一种建模场景。有很多种方法可以对这种旋转进行建模。在这篇博客中，我们将使用广义拉伸算子来解决这个问题，并讨论为什么这种方法有用。

一个真实案例：旋转烤肉

旋转物体暴露在载荷下的情况有很多种。例如， 在烤鸡或烤肉串时，暴露在热载荷下的旋转烤盘上的肉，通常使用的是煤块等辐射热源。旋转是对施加的热量进行分配的一种简单方法，它可以使烤盘所有区域不会变得过热或过冷，并且是帮助均匀烹饪的简单方法。

现在你是不是已经嘴馋了，让我们来看一个简单的案例吧。

激光加热的旋转硅晶圆

今天，我们来看一个激光加热旋转的硅晶圆案例。虽然它不像旋转的食物那样让人想起来就觉得很美味，但我相信你会发现它具有的一些相同信息。

你可能已经知道，COMSOL 模型库和 COMSOL 网站的案例下载页面中有一个这样的例子：一个安装在旋转平台上的晶圆，通过表面来回移动的激光加热。这个问题是在一个固定的坐标系中求解的(想象你站在加工室外面，看着晶圆在平台上旋转）。我们将它称为全局坐标系。

在这个案例中，激光被模拟成一个沿全局x 轴来回移动的热源，晶圆则围绕全局Z 轴旋转。晶圆的旋转是通过固体传热物理场接口中的平移运动功能来模拟的，它为控制的瞬态传热方程增加了一个对流项：

上述方程的右侧说明了晶圆的旋转情况，\mathbf{u}是速度矢量。这个速度矢量可以解释为材料进入和离开有限元网格中的每个单元，也就是说，我们是在欧拉坐标系上解决问题。由于几何形状是一个均匀的圆盘，施加的速度矢量描述了围绕圆盘轴线的旋转，这是一个有效的方法。

然而，缺点是当我们想在模型中加入更多的物理场时。平移运动功能只在传热物理场中可用，对于许多其他物理场接口，我们不想在欧拉坐标系中求解。

与其在全局坐标系的欧拉坐标系上求解这个问题，不如在拉格朗日坐标系上用一个随晶圆材料旋转而移动的旋转坐标系来求解。(你可以把自己想象成一个站在晶圆表面的小人，周围的环境将看起来是旋转的，而晶圆看起来是静止的）。

上述控制传热方程的右手边项变成了零，但我们现在需要考虑一个热载荷，它不仅沿全局X轴来回移动，而且还绕旋转坐标系的Z轴旋转。虽然这听起来很复杂，但实现起来却很简单。

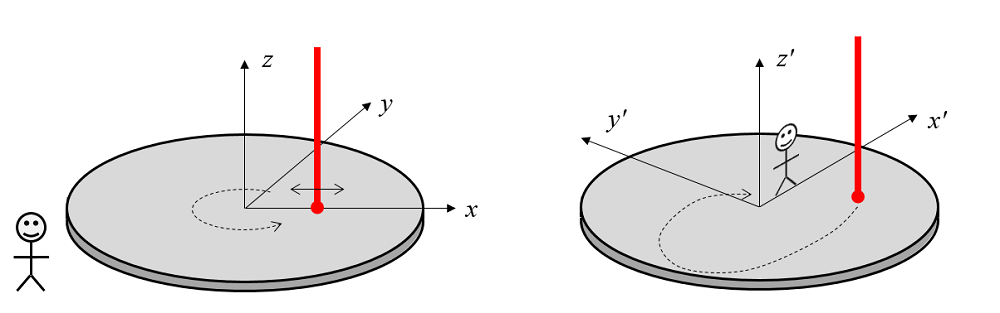
在全局坐标系中的观察者看到一个带激光热源的旋转晶圆沿着X轴来回穿行（左）。在与晶圆一起旋转的坐标系中的观察者看到晶圆是静止的，但热源在X-Y平面上以复杂的路径移动（右图）。

通过广义拉伸算子实现旋转

广义拉伸算子提供了一种将场从一个坐标系转换到另一个坐标系的机理。关于这类应用，我们已经介绍过，包括子模型,耦合不同的物理场接口，以及在一个移动点上评估结果。

在这篇文章中，我们将使用广义拉伸算子对施加的载荷进行旋转变换。模拟中的载荷是通过旋转矩阵给出的全局坐标系的坐标变换在旋转坐标系中施加的：

我们可以从已有的硅晶片激光加热的例子开始，简单地删除现有的平移运动特征。然后要添加一个广义拉伸算子，实现上述变换，如下面的截图所示。我们还想实现第二个算子来施加反向变换，即通过切换旋转的符号完成。

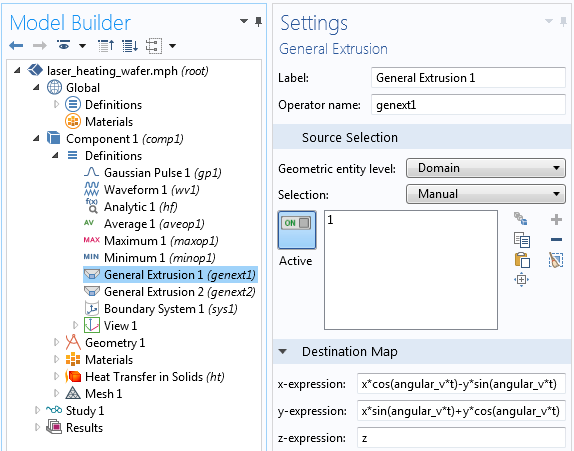
广义拉伸算子适用于旋转变换。

施加的热载荷是通过一个用户定义的函数 hf(x,y,t) 来描述的，该函数描述了激光加热载荷如何在全局坐标系中沿x 轴来回移动。这个移动的载荷通过广义拉伸算子转化为旋转坐标系，如下面的截图所示。

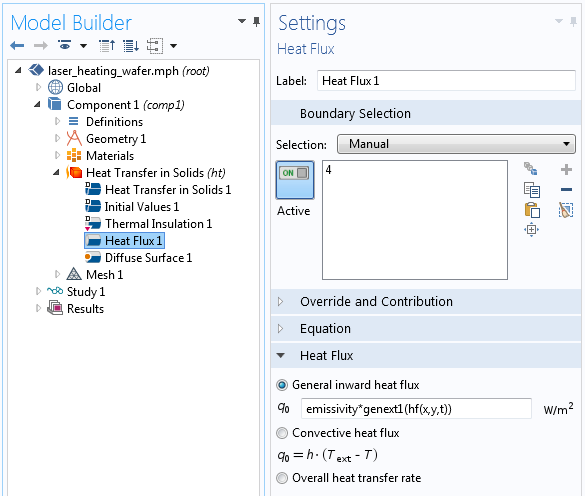
旋转坐标系中施加的热载荷，通过全局坐标系和旋转变换定义。

就是这样，你可以像以前一样解决这个模型。

现在的结果将是关于旋转坐标系的。对我们来说，通过使用施加反向变换的广义拉伸算子来绘制相对于全局坐标系的温度解可能更加实用。这样，我们将得到温度场的可视化绘图，就像我们站在加工室外面，用热像仪观察旋转中的晶圆一样。

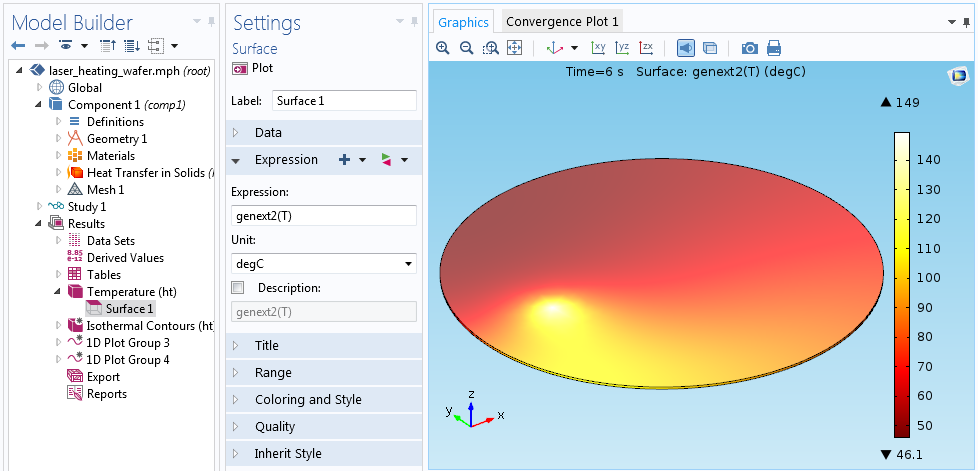
第二个广义拉伸算子用于将结果旋转回全局坐标系。

结束语

无论您使用的是平移运动功能还是广义拉伸算子，随时间变化的温度场模拟结果都是相同的。尽管广义拉伸算子需要更多的努力来实现，而且确实需要更长的时间来求解，但如果您感兴趣的不仅仅是热解，那就需要使用它。

例如，如果您还需要计算温度驱动的化学扩散和反应过程，或者在晶圆加热过程中热应力的演变，这些问题就应该在一个随着晶圆旋转的坐标系上解决。

当然，还有许多其他的应用可以使用广义拉伸算子，但我希望今天我所介绍的内容已经满足了你的需求。