
你是否正在进行 CFD 分析求解湍流问题?如果是的话,那么应该知道,得到数值解相当困难,要花费大量的计算时间。湍流模型方程中产生的非线性是引起这一问题的主要原因。黏度递变方法,先求解黏度较高的问题,将其解作为求解黏度较低的问题的初始条件,可以缩短计算时间。我们将向你展示如何利用 COMSOL Multiphysics 实现这种技术。
为什么增加黏度能提高 CFD 的收敛性?
在开始模拟任何流体的流动之前,通常会检查雷诺数,其公式为:
其中\rho是密度,\mu是流体的动力黏度。U是特征速度,d是模拟系统的特征长度。
雷诺数指流动时惯性力与黏性力之间的比值。计算出雷诺数有助于确定用 COMSOL Multiphysics 进行的是层流还是湍流分析。例如,在微流体通道中,特征速度和特征长度都相对较小,得出的雷诺数较低,所以这种流动是层流。相比之下,车辆周身气流速度较快,雷诺数较高,所以这种流动是湍流。你可以查阅之前的博客文章,了解关于流动的更多特性。
在使用 CFD 求解流体流动的问题时,找出湍流问题的数值解往往比求解层流问题更具挑战性。为了解其中的原因,我们来看一下求解的方程。对于湍流,COMSOL Multiphysics 会求解Navier-Stokes 方程形式的雷诺平均 Navier-Stokes(Reynolds-averaged Navier-Stokes, 简称 RANS)公式。RANS 公式引入了一个新变量,即湍流黏度,用来描述流动时的湍流等级。计算湍流黏度时,会使用本软件仿真中应用的湍流模型所定义的其他方程。
例如,k-ε 湍流模型利用湍流动能(k)和湍流耗散率(ε)计算湍流黏度。湍流模型方程与 Navier-Stokes 方程形式相似,都含有线性项和非线性项。湍流方程中出现的非线性问题是高雷诺数仿真更难以实现收敛的原因。要了解选择哪种湍流模型的更多信息,请查阅这篇博客文章。
所以,对于高雷诺数的仿真,我们必须使用湍流模型,并利用 COMSOL Multiphysics 求解高度非线性的方程。一开始就设置一个良好的初始条件有助于使非线性问题收敛,如此处所述。流体黏度决定了方程的非线性程度。我们先求解黏度较高的模型,即求解更可能收敛的弱非线性问题。然后,为了提高收敛性,将求解得到的高黏度结果作为真正要求解的低黏度问题的良好初始条件。这一方法称作黏度递变。
借助黏度递变方法,先求解黏度较高的流体模型,然后逐渐降低黏度进行求解,直到期望值,因此需要求解一系列模型。黏度较高问题的解用作求解下一个黏度较低问题的初始条件。先求解黏度较高的模型,也就是雷诺数更低的模型。由此我们先从更易收敛的弱非线性模型开始。逐步降低黏度(从而提高雷诺数),使其回到原始值,我们将弱非线性问题的求解转变成对强非线性问题的求解,通过这一过程最终获得初始模型的答案。接下来看一看如何在 COMSOL Multiphysics 中进行操作。
利用 COMSOL Multiphysics 实现黏度递变
假定 COMSOL Multiphysics 中已建立了一个 CFD 模型,并且希望提高其收敛性。黏度梯度技术包括三个步骤:
- 创建递变参数
- 将黏度与递变参数相乘
- 在研究中定义递变参数的辅助扫描
首先,定义要与黏度相乘的新参数。我们在参数中设置的“visc_ramp”值并不重要,因为随后定义的辅助扫描会覆盖这个当前值。
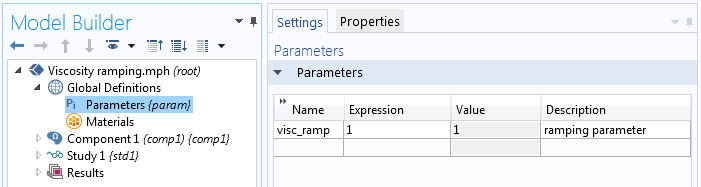
定义此参数。
转至材料节点,将流体黏度与“visc_ramp”相乘。比如,如果“visc_ramp”的值为 100,则表示要求解流动问题的流体黏度比初始值高 100 倍。最终当“visc_ramp”值达到 1 时,便回到材料的实际黏度进行求解。
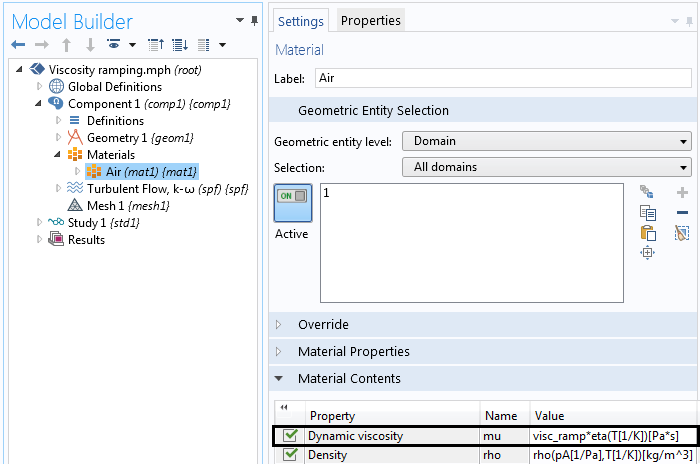
黏度与“visc_ramp”相乘。
“稳态”研究步骤中,我们为“visc_ramp”创建一个辅助扫描,并将扫描的数值定为 1000、100、10 和 1 。辅助扫描会求解第一个“visc_ramp”值(1000),将它的解作为求解下一个“visc_ramp”值(100)的初始条件。我们以相同的方式持续扫描,直到“visc_ramp”达到 1,即求解流体实际粘度。
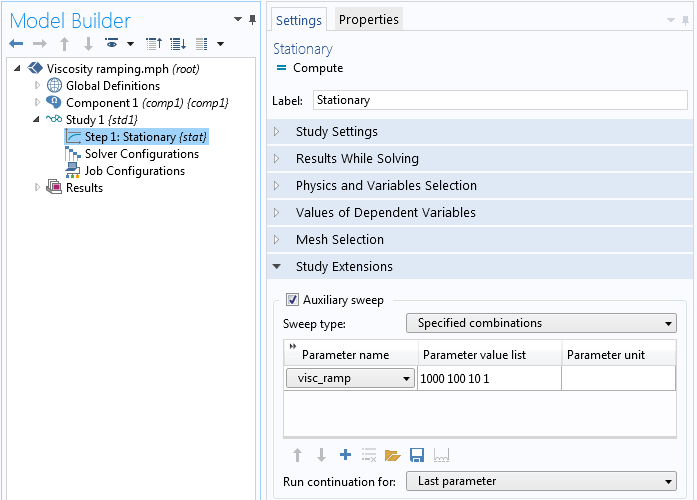
“稳态”研究步骤。
在计算这个研究时,进度选项卡会显示当前正在求解的“visc_ramp”值。最后,解实现收敛,我们即可查看结果。
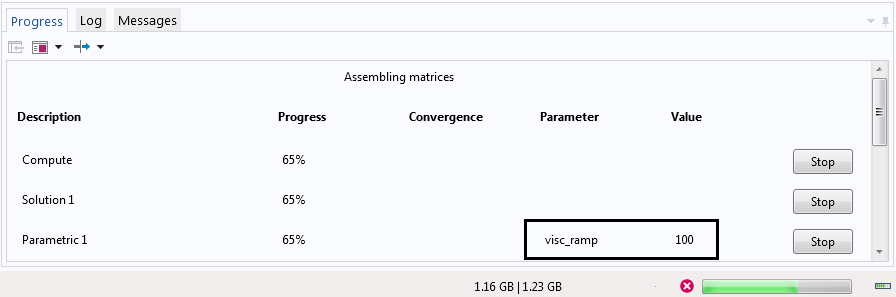
“进度”选项卡显示正在进行“visc_ramp”值为 100 时的计算。
黏度递变过程图显示如下。该图显示后台阶流场中湍流的流线与速度,图像来源于案例下载示例。
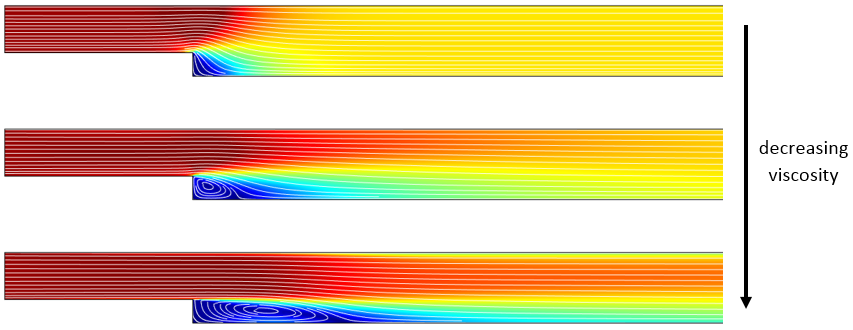
三种不同黏度时后台阶流场中湍流的流线与速度图。
选择扫描的递变参数
在多数情况下,开始时将递变参数设为 100 或 10 就足以实现收敛。不过在有些收敛难度更大的情况中,建议将黏度梯度参数的初始值设为较高值,随后每次降低一个数量级(例如,1000、100、10 和 1)。
现在,我们先从一个黏度较高的流体(1000)开始,然后定义“visc_ramp”的中间值(100 和 10),再使求解器过渡到实际流体黏度(1)。如果求解器找不到下一个较低黏度的解,那么可以尝试使用上一个收敛值和下一个用户指定值之间的中间值,这个过程称为回溯。
为演示回溯,我们在“visc_ramp”值为 1000 和 1 时分别运行辅助扫描。在求解递变参数 1000 后,软件会尝试用递变参数 1 进行求解。一旦求解器注意到未实现收敛,就会开始回溯,尝试使用递变参数的中间值(本案例中为 501)。如果回溯参数值 501 能够使解收敛,那么求解器会再次尝试用递变梯度参数 1 求解,这一次成功在望!
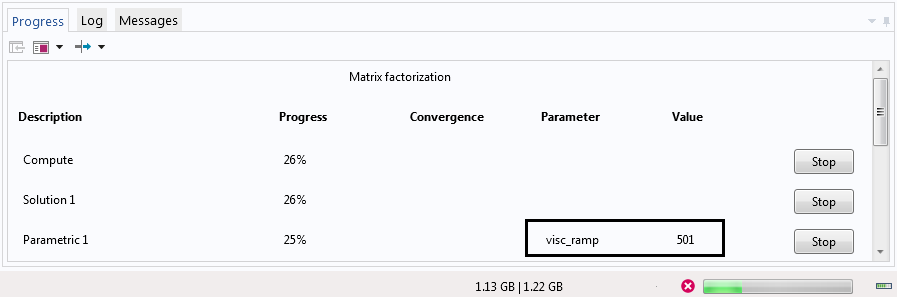
“进度”选项卡显示“visc_ramp”设为 501 时进行的计算。
回溯是帮助求解器在辅助扫描中提高收敛性的很有价值的软件内置技术。不过,用户仍需指定扫描的中间值,便于求解器从高递变值过渡到低递变值。
在有些情况中,求解器使用了回溯法,但在值大于 1 时仍未收敛。这个现象通常表明网格过于粗化,无法解算流场。遇到这种情况时,应先细化网格。另外,请牢记在模型验证过程中一定要执行网格细化研究。
黏度递变和非线性递变的强大功能
我们已这篇博客文章中展示了如何在 COMSOL Multiphysics 中利用黏度递变协助完成 CFD 模型的收敛。为此,我们建立了连续性研究,从弱非线性问题着手,逐渐增强非线性,直至求解出初始问题。在求解 CFD 问题时,如果需要使用湍流模型且雷诺数很大,则黏度递变技术相当有用。
非线性递变技术的应用多种多样。例如,除黏度递变外,我们还可以逐渐减小自然对流问题中的重力,或者逐渐减小非牛顿流体流动中的流动特性指数“n”。这一技术还可广泛用于任何非线性物理场问题中,如此处重点讨论的问题。
在一个与非线性递变相似的过程中,我们可以转而逐渐减小系统中的载荷,从而提高其收敛性。流体流动中载荷的递变通常意味着入口速度逐渐减小,这是另一种须牢记的技术。
要了解更多相关技术并应用到 COMSOL Multiphysics 仿真中吗?请立即联系我们。



评论 (0)