
今天这篇博文,我们继续对电压和接地这两个术语进行讨论。 文中,我们将定义正弦时变模型并解释这些术语。以传输线为例,讨论如何在涉及波状场的问题中正确定义电压和接地。
一条简单的传输线
假设有一根位于地表面(或地平面,或信号地)上方的自由空间中的金属线,如下图所示。我们将对它进行更精确的定义。这属于 TEM 传输线的范畴,意味着电场和磁场完全位于垂直于该线的平面内,并且坡印廷矢量与这条线处处平行。(非常严格地说,这是一条准 TEM 传输线,因为金属线不是无限导电的,但正如我们将看到的,这一点对我们下面讨论的内容并没有任何影响)。
在电线的一端,有一个正弦时变源将接地层连接到电线,在电线的另一端,有一个电阻负载。虽然我们在实践中并不经常看到这种精确的传输线,但它与微带线非常相似。
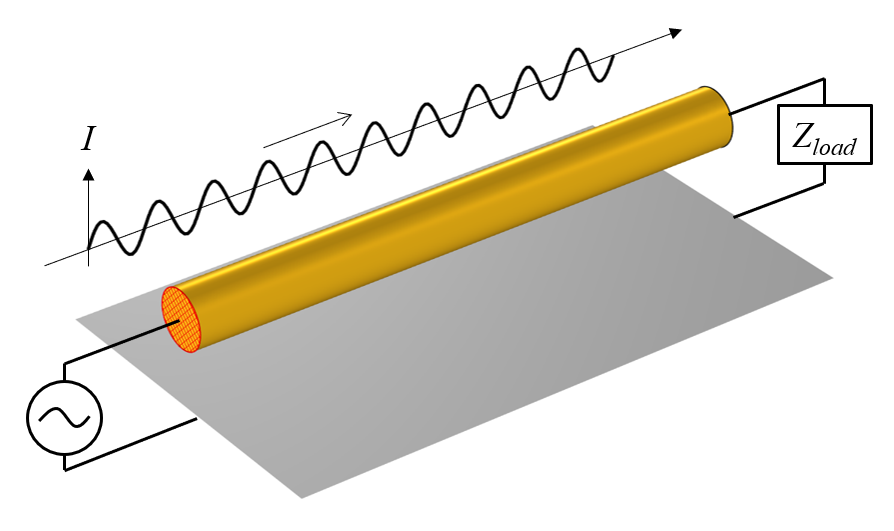
接地面上方的导线,一端是电源,另一端是负载,以及导线中某一时刻的总电流图。
正弦时变源将驱动电流沿整个导线来回移动,通过电阻负载,然后进出接地平面。如果我们可以在任何时刻对电流进行快照,它看起来就像是从源到负载传播的正弦波。
现在,当我们考虑流经导电材料的时变电流时,必须考虑集肤效应:即时变电流在导体外表面流动的趋势。事实上,我们将假设激励频率很高,与导线的半径相比,集肤深度非常非常小,小到我们看作电流是在导体的表面上流动,而不是在体积内流动,并且可以通过阻抗边界条件对导线进行建模。这在以前的博文“模拟电磁波问题中的金属对象”和“如何模拟时变磁场中的导体”中有过更加详细的讨论。
接下来,我们来看地表面。回想一下我们之前的定义,在直流系统中,我们将接地定义为对电流没有阻力的域(或者至少阻力很小,以至于与我们的建模目的无关),这里也适用类似的定义。接地是一个没有电阻的域的边界,或者它是一种完美的导电材料。然而,正如刚才所讨论的,由于存在集肤效应,对于具有无限电导率的材料,集肤深度恰好为零,因此在接地线表面上将有电流流动。
地平面上的情况
现在,让我们来讨论以下直流系统和波状场系统之间的巨大区别。在直流系统中,我们完全忽略了接地域内的电流;而波状系统中存在沿这个地表面流动的电流,这些电流不能被忽略。下图是这些电流以及一个导线横截面上的电场和磁场在某个时刻的可视化效果图。
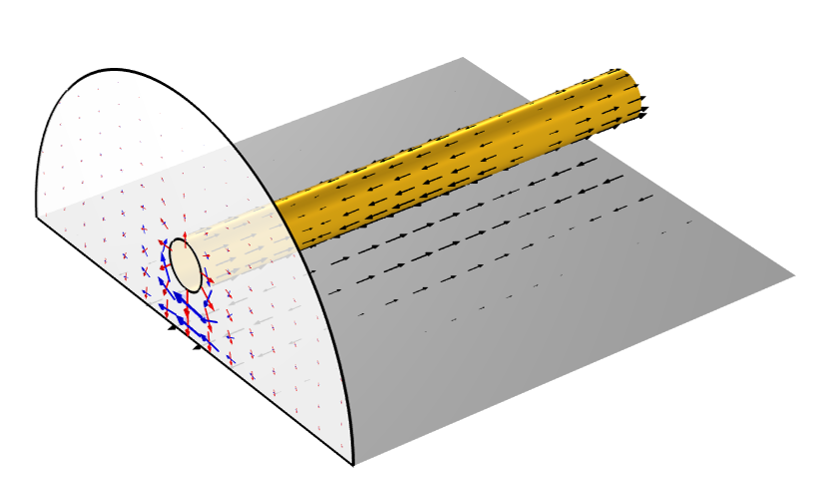
某一瞬间的电流(黑色)、电场(红色)和磁场(蓝色)的可视化箭头。
也许有人会问:在一个有无限电导率的材料表面,怎么会有有限的电流?要回答这个问题,我们还需要看一下地平面上方的自由空间。这个自由空间有一个阻抗,而沿着材料表面流动的电流将取决于这个自由空间的阻抗。
这立即提出了一个非常重要的问题:我们必须考虑地平面上方有多少可用空间?事实证明,我们不仅要考虑地平面正上方的自由空间,还要考虑导线周围的空间,甚至导线上方的一些空间区域。所有这些结构都会对传输线的阻抗产生影响。事实上,在建立这类数值模型时,需要研究要包括多少范围的自由空间区域。COMSOL 案例库中的确定平行传输线的阻抗教程模型对此有所讨论。
由上述教程模型可知,这个完美电导体表面(我们称之为地平面)上的电流会受到它上方所有空间的影响。另一种说法是这个完美电导体表面上的电流包含整个建模空间的图像,这使我们对 PEC 地平面有了第二个解释:它是一个对称性条件。就好像平面的另一边有一个等效的结构,而在那一边,导线中的电流将指向相反的方向。
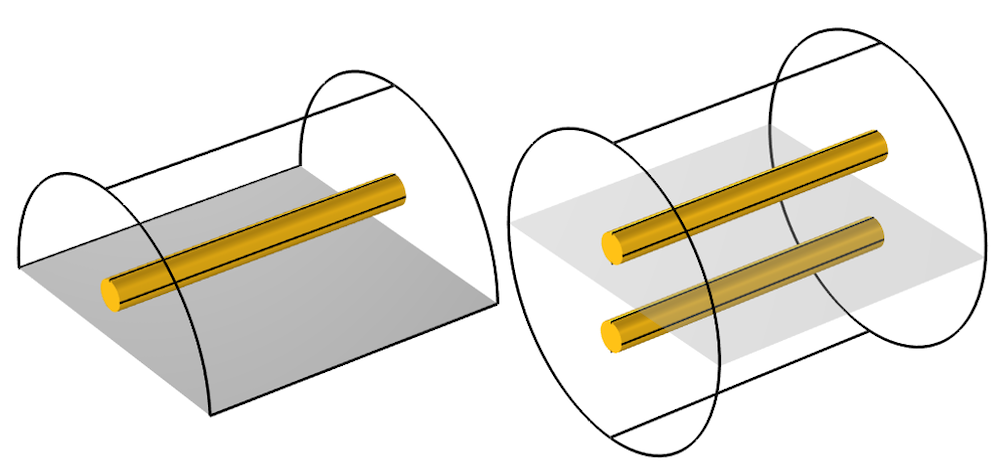
通过对称性条件,地平面上方的导线模型等效于平行导线传输线的模型。
基于此,在电磁波的范围内,我们现在可以开始做一些更精确的定义。地面是一个无损(完全导电,或完美电导体)的表面,有限的电流沿着它流动。沿着这个表面流动的电流将受到它上方所有结构的影响。如果这个完美电导体表面在建模空间的一侧描述了一个平面,那么就相当于强加了一个对称性条件。如果我们有两个分离的完美电导体表面,可以任意选择一个,并将其定义为接地。在某些情况下,我们还可以想出一个办法来定义第二个完美半导体表面相对于这个接地的电势差(电压)。
在频域中定义电压
回想一下我们对稳态电流的讨论,我们将电压定义为任意两点之间电场的路径积分。对于稳态电流,电场是标量电势的梯度,并且该积分始终与路径无关。然而,对于电磁波,电场是波动方程的解,并且我们可以证明(通过一些我们将跳过的繁琐矢量计算)这种电场的路径积分与路径无关,除了一些特殊情况。
其中一个特殊情况是,当沿着位于完美电导体表面的一条线进行路径积分时。与表面相切的电场始终为零,因此沿该表面任何一条线的电场积分为零。然而,表面电流被定义为\mathbf{J = n \times H},其中\mathbf{ H}由\mathbf{\nabla \times E}= -j \omega \mathbf{H}计算,所以电流不为零,即使切向电场的积分为零。请注意,这里没有矛盾;周围环境的阻抗导致完美电导体表面的电流有限,且切向电场为零。
第二个要考虑的有趣情况是,当我们沿着垂直于TEM传输线轴线的平面上的一条线取电场的路径积分时。根据定义,电场和磁场完全位于这个平面内,所以可以证明(通过一些我们将跳过的矢量计算)这个积分将与路径无关。也就是说,我们可以在这个平面的各点之间定义一个电压。因此,选择一个接地表面上的点,并在传输线的电线上的另一点,进行任何路径积分。现在我们有一个电压,对应于从信号分析仪得到的测量结果。我们也可以沿着完全分割接地和导线之间空间的线,对磁场进行路径积分,得到沿传输线流动的电流。
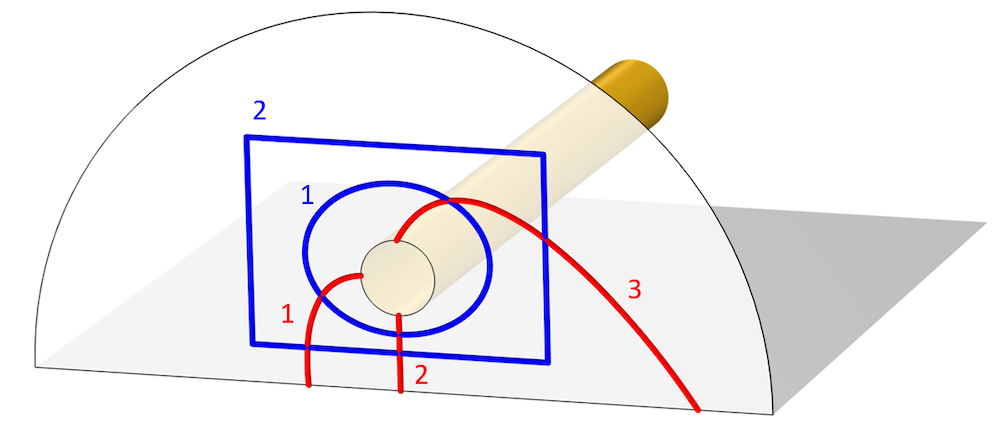
显示电压(红色)和电流(蓝色)的各种不同积分路径的图像。
最后,我们来讨论这样一个事实:由于导线的有限导电性,这实际上是一条准TEM线,可以通过阻抗边界条件进行建模。在这种情况下,电场和磁场的平面外分量相对于平面内分量来说非常小,我们仍然可以安全地使用上述定义。
综上,我们知道:
- 电压是电场的路径积分,但这只能在电场旋度为零或接近零的情况下进行评估:在 TEM 或准 TEM 传输线的横截面上。
- 在 TEM 或准 TEM 传输线的横截面上,电压对应于通过信号分析仪物理测量的电压。只有在这里,术语电压在频域电磁波模型中才有意义。
- 在 PEC 表面,我们可以沿着该表面上的路径对电场进行积分,但是如果沿着不在该表面的路径进行积分,可能会得到一个非零积分。另外,我们已经看到会有电流存在,所以两点之间的零电压差并不意味着零电流。因此,实际上,在这种情况下谈论电压几乎没有价值。如果我们试图实际测量两点之间的场,我们将不得不引入一个传感器,包括这些点之间的某种传输线,但这会改变设备。
请将上述这些信息牢牢记在大脑中,这样我们就可以自信地建模了。对于这里的情况,我们可以使用TEM型的端口边界条件,将接地和电势子特征应用于接地平面和电线的边缘。COMSOL学习中心的一篇文章“对 TEM 和准 TEM 传输线进行建模”中提供了对 TEM 类型传输线建模的所有其他选项的完整概述,您可以参考阅读。
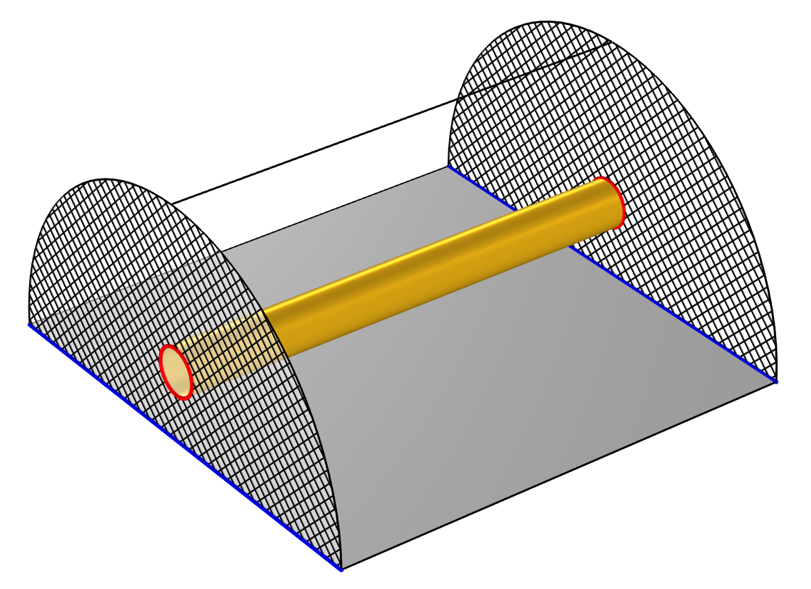
传输线模型的设置示意图。两端的两个 TEM 端口(交叉阴影线)定义了接地(蓝色)和电压(红色)。
结束语
现在你知道如何在频域电磁波建模的背景下自信地使用电压和接地这两个术语了吧!我们可以把同样的论点扩展到瞬态情况下,并得出同样的结论。在时域建模中,接地是一个电流返回路径,可以是一个对称条件。
因此,对于任何时变模型,同时考虑电场和磁场,只能在评估 TEM 传输线横截面的场的情况下谈论电压。尽管这句话很简单,但这个我们必须遵循的论点对于理解电磁设备的建模非常有帮助。
后续操作
单击下面的按钮,在相关的学习中心文章中获取有关模拟 TEM 和准 TEM 传输线的详细演示,其中包括逐步建模说明和软件屏幕截图:



评论 (0)