电准静态理论
时变电流
对于时变电场和电流,在磁效应可以忽略不计的情况下,可以通过电流守恒方程:
(1)
与高斯定律:
(2)
组合得到恒定电流方程:
(3)
假设场的变化足够平滑,可以将它重组为:
(4)
其中的总电流包含位移电流,写为:
插入线性材料的本构定律:
(5)
且:
(6)
从而得出:
(7)
再插入电势方程:
(8)
可以得到:
(9)
请注意,通过使用电势,隐含地假设了其中没有磁效应。
材料界面的时变电流方程和边界条件
下表总结了电准静态的基本边界条件:
| 方程名称 | 微分形式 | 积分形式 | 边界条件 |
|---|---|---|---|
| 电流守恒 | |||
| 法拉第定律(恒定电流) |
其中, 是总电荷,
是沿面法向的电流。
时谐场
当场随时间呈正弦变化时,电准静态方程可以用相量进行简化,这是一种场量,可通过使用复值表达式对大小和相位信息进行编码。在使用相量时,需要考虑场量随时间演化的傅里叶展开;比如电势:
(10)
其中,高阶项包含与 、
等成比例的谐波。
在正弦场中,谐波会消失,只剩下零(常数)阶和一阶傅里叶项。
时谐电流
如果将零阶项代入线性材料的电准静态方程,则由于 的时不变性,结果得到恒定电流守恒方程。此外,由于材料和方程的线性特性,零阶和一阶部分可以单独处理。因此,所需的其余方程由谐波(一阶)项组成:
(11)
通过让时间导数只对时变部分起作用,并利用指数函数总是非零这一事实,该表达式可以简化为:
(12)
在上式中,隐含地假设材料具有时不变特性。此外,通过从电势场中去掉下标 1,可以使符号表示得到简化。此方程是电准静态方程的时谐版本,其中的电势为相量,可能具有非零相移,因此为复值:
(13)
以下物理量:
(14)
可以解释为复数电导率。
此版本的电准静态方程是恒定电流方程的时谐泛化版本:
(15)
其中:
(16)
为时谐电流密度。
上式也可以写为:
分别包含传导电流密度和位移电流密度贡献。在材料界面处,电流的连续性条件为:
在外表面没有法向电流且 的重要情况下,该条件变为:
换句话说,材料界面上的连续性条件与静电情况相同。
时谐静电
将电准静态方程除以 可以得到另一个版本的方程:
(17)
其中的量:
(18)
可以解释为复数介电常数。
此版本的电准静态方程是静电方程的时谐泛化版本:
(19)
其中:
(20)
为时谐位移场。
时谐公式综述
下表列出两个时谐电准静态方程以及相关的材料属性和本构关系:
| 方程名称 | 方程 | 材料属性 | 本构关系 |
|---|---|---|---|
| 时谐电流密度 (时谐电流) |
|||
| 时谐位移场 (时谐静电) |
从上表可以看出,在频率趋近于零的极限下,第一个方程仍可准确定义,并成为恒定电流方程。另一方面,在这个极限下,复介电常数的虚部对于第二个方程变得无界。不过,如果材料是理想绝缘体,即电导率为零,则第二个方程变得与频率无关,这时与静电情况相同。
这表明,在静态工况下,电流守恒方程对于理想导体()的建模非常有用,而静电方程则适用于理想绝缘体(
)建模。对于频率足够低的良导体来说,只要
,即可忽略时谐电流密度方程的虚部。同样,对于良好的绝缘体来说,有时可以忽略时谐位移场方程的虚部;但对于在较高频率下使用的某些材料而言,损耗(
)变得与频率有关,此时虚部就非常重要。

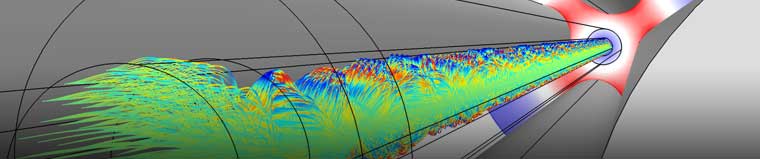
四极质谱仪中的离子轨迹。这种类型的光谱仪利用静电势和时谐电势的巧妙组合对粒子进行分类,。通过调节谐波频率(本例为 4 MHz)以及静电场和谐波场的强度,只有一定质量的粒子能通过该设备进行传输。
四极质谱仪中的离子轨迹。这种类型的光谱仪利用静电势和时谐电势的巧妙组合对粒子进行分类,。通过调节谐波频率(本例为 4 MHz)以及静电场和谐波场的强度,只有一定质量的粒子能通过该设备进行传输。
上次修改日期:2019 年 2 月 13 日
