电磁学静电学

自由空间中的静电

静电学是电磁学的一个子领域，研究静（非运动）电荷引起的电场。我们首先从自由空间开始讨论，假设空间电荷密度为，它与电场的关系式如下：

⁽¹⁾

其中，是自然界的一个普适常数，称为自由空间的介电常数。

这一关系意味着，在静电学中，空间电荷密度相当于一个体积源。只有电荷-电场关系是不够的，但麦克斯韦方程组隐含了一个额外要求，即电场为无旋场（无旋度）：

⁽²⁾

这是用于描述静电场的法拉第定律。

无旋场存在一个标量势，由此可以得到电势的定义：

⁽³⁾

对于任何足够平滑的标量场来说，总会满足以下矢量恒等式，确保电场为无旋场：

⁽⁴⁾

电势前面的负号是传统约定。

通过组合以上表达式，只用一个方程即可描述麦克斯韦静电方程中包含的信息：

⁽⁵⁾

由于此方程不能表示电介质材料，因此在工程领域的应用有限。为了解决这个问题，我们利用感应极化效应对该理论进行扩展。

电介质材料中的静电

理想化电介质材料的特点在于其中没有任何自由电荷，而只有束缚电荷。在微观层面，这些束缚电荷可以被外部电场所取代，从而产生感应电偶极子。这些感应电偶极子是成对的正负电荷，在某种程度上与电场方向一致，导致电介质材料内的电场与自由空间的电场不同。为了从宏观上描述这种现象，我们可以方便地引入极化矢量场和极化电荷密度，其关系式为：

⁽⁶⁾

根据下式，极化效应会局部改变材料内部的电场：

⁽⁷⁾

或等价于：

⁽⁸⁾

在此基础上，我们可以引入一个新的基本量，即电位移场，定义为：

⁽⁹⁾

利用这一定义，静电方程（也称为高斯定律）可以变为：

⁽¹⁰⁾

为了充分描述静电现象，我们仍需保留电场无旋（法拉第定律）条件。由于此条件用电势来描述，因此静电方程组可以联立成一个方程：

⁽¹¹⁾

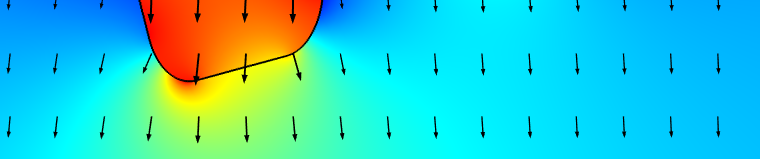
介电常数大于周围环境的物体附近的电场。这两幅图显示位于两块电容板（未显示）之间，被空气（）包围的电介质体（）。顶部和底部电极分别具有正电位和负电位。左图用不同的颜色来显示电场大小，并用箭头表示其方向。右图用不同的颜色来显示电位移场幅值，也用箭头表示方向。红色和蓝色分别表示高低幅值。

介电常数小于周围环境的物体附近的电场。这两幅图显示位于两块电容板之间，被电介质材料（）包围的气腔（）。顶部和底部电极分别具有正电位和负电位。左图用不同的颜色来显示电场大小，并用箭头表示其方向。右图用不同的颜色来显示电位移场幅值，也用箭头表示方向。红色和蓝色分别表示高低幅值。

线性电介质材料

在静电学中，人们常常可以假设材料呈线性，这预示着极化矢量场与电场成正比：

⁽¹²⁾

其中比例常数为电极化率。

当材料呈各向异性时，极化率可以是一个 3x3 的张量：

⁽¹³⁾

将其代入与的关系式中，得到：

⁽¹⁴⁾

我们还可以引入两个有用的新量：相对介电常数和绝对介电常数。

线性电介质材料最重要的本构关系假定为：

⁽¹⁵⁾

各向异性极化率对应于各向异性相对介电常数：

⁽¹⁶⁾

这意味着对于某些材料而言，和场可能不完全一致。

利用静电势，我们可以将线性材料中的静电基本方程写为：

⁽¹⁷⁾

材料界面的静电方程和边界条件

高斯定律和法拉第定律可以分别看作是为电场散度和旋度指定条件。根据亥姆霍兹定理，这可以确定电场所能达到的场强常数。顺便指出一点，由于这个未知常数，我们最终必须指定电势的地电平。在材料界面处，散度条件表示电场法向分量的条件，旋度条件表示电场切向分量的条件。材料界面表明存在不连续，为了方便理解要对边界施加何种条件，我们通常使用对应的积分形式。然后，通过分别采用闭合面的收缩极限（高斯定律）和封闭等值线的收缩极限（法拉第定律），使材料的界面形成封闭，导出边界公式。

下表对此进行了汇总：

方程名称	微分形式	积分形式	边界条件
高斯定律
法拉第定律（静电）	,		,

其中，是体积电荷，是材料界面处的表面电荷。

左侧仿真显示理想导电金属物上的感应表面电荷密度，右侧仿真显示电势。在右图中，红色和蓝色分别表示正电势和负电势。顶板和底板均保持固定，但具有不同的电势。中间的闭合面具有感应产生的恒定浮动电势，由于对称性，其值为两块板的电位平均值。表面电荷密度的分布使每个金属表面均为等势面，这是高斯定律的一个推论。

通过文字表述来汇总这些方程的含义可以帮助你加深理解：

方程名称	微分形式	积分形式	边界条件
高斯定律	所有电场线都始于电荷，并终止于电荷。	通过闭合面的总通量等于其所包围的电荷。	材料界面的表面电荷等于位移场法向分量的跃迁。
法拉第定律（静电）	电场为无旋场。	电场守恒。	在整个材料界面上，电场的切向分量是连续的。

需要注意的是，对于时变情况，电场不再是无旋场，并且法拉第定律会得到一个与电磁感应对应的附加项。

静电能

电场中包含的静电能可以用许多不同的方式来表示。对于电介质，某一体积（）内的静电能可以用场量表示为：

其中，静电能量密度定义为：

请注意，对于静电能量密度的定位，相关的物理说明比较有限（另请参见：The Feynman Lectures on Physics, Volume 2）。

另一个用体积电荷密度和局部电势来描述静电能的表达式为：

这两个能量表达式被证明是等价的。

在计算静电力和电容值时，静电能的概念非常有用。

发布日期：2019 年 2 月 14 日
上次修改日期：2019 年 2 月 14 日