结构力学响应谱分析

什么是响应谱分析？

响应谱分析是一种结构响应分析方法，用于评估结构对短暂、不确定的瞬时动态事件产生的响应，例如，地震和冲击便是这类事件的典型例子。由于我们不知道载荷的确切时间历史，因此很难执行瞬态分析。此类事件的持续时间短，不能被视为各态历经（“平稳”）过程，就这一点来说，随机响应方法也不适用。

响应谱法基于一种特殊类型的模态叠加，其思路是提供一种输入，从而对具有特定的固有频率和阻尼的特征模态能够被此类事件激励的程度进行一定的限制。

本文分为三部分：

• 响应谱的定义
• 根据给定的时间历史生成响应谱
• 给定响应谱在结构分析中的应用

大多数情况下，负责执行响应谱分析的工程技术人员会得到给定的设计响应谱，此时可以将前两个部分作为背景材料。

响应谱定义

响应谱是频率或周期的函数，表示简谐振子在受到瞬态事件作用时的峰值响应。响应谱是振子固有频率及其阻尼的函数，因此，它不是激励的频率部分的直接表示（如傅里叶变换），而是信号对单自由度（SDOF）假设系统的影响。

SDOF 系统分析

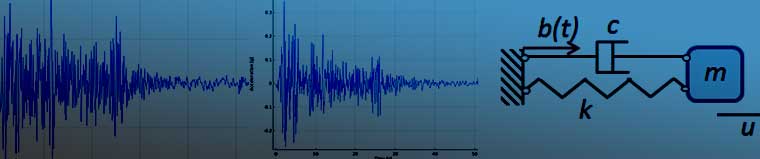
我们以一个连接到动基座的质量弹簧阻尼器系统为例。基座具有给定的运动参数。

在没有外力的情况下，质量块的运动方程可以写为

除以质量并使用常规符号，可以得到

这里的无阻尼固有（角）频率为

阻尼比为

可以看出，支撑运动是一个强迫项，解只取决于两个参数：和，而与单独的m、c和k值无关。

您可以选择质量块与基座之间的相对位移代替绝对位移作为自由度。这实际上是一个坐标系变换，其中振子在连接到基座的坐标系中进行研究。就像在任何加速坐标系中一样，其中会产生惯性力。运动方程可以表述为

(1)

因此，支撑加速度表现为类似重力的载荷。这种表现形式有两个优点：

• 系统中的内力（即弹性力和阻尼力）取决于相对位移和速度，不受刚体运动的影响。
• 通常，我们可以根据加速度图得到测量数据，因此不直接使用基座位移。

对于给定的、和值，求解此方程需要足够长的时间。位移、速度和加速度响应谱定义为加速度历史产生的最大值。

这些都是相对频谱。通过改用绝对位移，可以对绝对频谱进行类似的定义。

有时，正频谱与负频谱会有所区别，因此

速度谱和加速度谱也是如此。

速度响应谱和加速度响应谱通常可由下式近似得到

这种频谱称为伪速度谱和伪加速度谱。

对于无阻尼系统，基于相对位移的伪加速度谱实际上等于绝对加速度谱，这一点从无阻尼运动方程可以看出来，

从而得到，

因此，相对位移的最大绝对值必须和绝对加速度的最大绝对值同时出现，两者之间的比例因子为。对于低阻尼系统，这种关系仍近似成立。由于大多数机械系统都具有低阻尼（一般为 2% 到 5%），我们通常假设绝对加速度和伪加速度的频谱相同。

描述这种情况下的阻尼的另一种常见方式是使用Q 因子（品质因子），与阻尼比的关系由下式给出

如何创建响应谱

对于特定给定的时间历史，可以通过以下方式创建响应谱：

1. 选择生成频谱所需的频率范围
2. 选择一个频率步进，确定响应谱中应计算的点数
3. 选择特定的阻尼比
4. 对于每个选定的频率
   a. 在足够长的时间内用求解方程（1）
   b. 跟踪并存储的最大值

该方程可以用纯数值时间步进求解，但可能还有更好的求解方法。如果给定为加速度图中的多个点，则可以很自然地假设加速度在这些点之间呈线性时间变化。因此，对于两次测量之间的每个间隔，例如从到，振子的运动方程如下

方程右边是线性时间函数，您可以对每个时间间隔进行解析求解。初始条件可从上一间隔的最终状态获取。

实际上，最大值可能出现在驱动事件结束之后。当的值较小（长周期）时会发生这种情况。所以，如果振子已经停止运动，时间步进必须至少持续一个完整的周期。

您可以通过此公式跟踪以下参数的极值：

• 相对位移
• 相对速度
• 相对加速度和绝对加速度

由于只有已知，而和未知，因此无法得到绝对位移和绝对速度。当然，可以通过对加速度进行时间积分来恢复基础速度和位移。然而在实践中，积分可能会引起漂移，因此最终速度和位移都非零。由于非零的最终位移和速度都是非物理量（至少对于许多类型的事件来说是如此），因此必须进行一定程度的数字滤波。对于冲击来说还有一个问题，那就是应该为基础位移和速度选择什么初始值。

示例 1：半正弦冲击

在许多标准中，对冲击的一般描述通常采用半正弦加速度脉冲，其幅值和冲击持续时间可以是不同的值。例如，加速度可以是 20 g、50 g 或 100 g（g = 9.8 m/s²），持续时间可以是 6 ms 或 11 ms。在本例中，我们使用持续时间为 11 ms 的 50 g 半正弦脉冲作为加速度。

阻尼为 5%（Q = 10）的响应谱计算结果如下图所示。

绝对加速度的最大值出现在与输入信号的频率组成相似的频率处。在本例中，当频率为 74 Hz（T = 13.5 ms）时达到峰值。在高频情况下，加速度谱趋于 50 g。这是对任意信号的一般观察：在高频下，振子将表现为刚体，因此质量块仅跟随基座运动。如此一来，绝对加速度谱的渐近值总是等于事件持续期间的峰值基座加速度。

在低频情况下，加速度趋于零，其速率与频率成反比。对于非常软的振子，基座运动只会压缩弹簧，不会使质量块产生明显的运动。

我们还可以看出，这种情况下的伪加速度谱与实际的绝对加速度谱几乎没有区别，即使阻尼为 5% 也是如此。

下图针对振子固有频率的三种不同选择显示其时间响应，对应于上述响应谱中的标记。

• 频率为 15 Hz 时，载荷脉冲只提供较小的初始推力，振子随后在其固有频率下经历自由振动。峰值加速度出现在激励结束后很长一段时间内。
• 频率为 75 Hz 时，出现最大动力放大效果。载荷脉冲基本上与相对速度同相，它为系统提供最大能量输入。
• 频率为 500 Hz 时，振子在很大程度上充当刚体，紧密跟随基座加速度。峰值加速度与基座加速度几乎相同。

相对位移谱如下图所示。这与上述加速度谱基本相同，但按比例因子进行缩放。

接下来，我们比较一下相对速度谱和伪速度谱。从图中可以看出，二者差异非常大。伪速度谱和伪加速度谱不代表真实的相对谱。这是一般性观察，伪谱应视为位移谱的不同表示。

一种简便的响应谱表示方法是采用三联或四轴图。在此类绘图中，可以同时显示相对位移、伪速度和伪加速度。这是因为它们分别通过频率因子和频率的平方进行关联；而在对数图中，则仅显示斜率不同的线。三联图本质上是伪速度图，但有两组额外的斜栅格线，分别表示位移和加速度。

半正弦脉冲的响应谱实际上不够典型，原因是这种脉冲只有正加速度。如果这种脉冲相对于时间进行积分，则它对应的结果是非零速度和不断增大的位移。大多数事件（如地震）在发生前后的位移和速度都为零。如果使用完整的正弦脉冲代替半正弦脉冲，也可以得到低频特性衰减。

示例 2：El Centro 地震

人们研究最多的地震记录之一是 1940 年 5 月 18 日发生的“El Centro”地震。记录的信号（带有一些滤波）如下图所示。

El Centro 地震中的南北方向加速度（左）和东西方向加速度（右）。通过美国工程强震数据中心（Center for Engineering Strong Motion Data，简称 CESMD）访问的强震数据，提供这些数据的网络或机构是加州强震观测计划（CSMIP）和USGS 国家强震动工程（NSMP）。*

对于响应谱分析相关的事件来说，这些曲线非常典型。通过对信号的肉眼观察发现，主频率组成在 1-3 Hz 范围内，而事件主要部分的持续时间约为 30 s。因此，这些条件不能被视为稳态。另一方面，还存在大量循环（100 阶），这可以激励一个共振频率在 0.5-30 Hz 范围内的结构。

下图显示阻尼为 2% 和 5% 时计算的响应谱。

响应谱表现出一些有趣的一般属性。阻尼越高，响应值越低，频谱越平滑。这些属性都离不开一个事实，即振子的频率响应在阻尼较高时具有较低但较宽的峰值。

此外，南北方向和东西方向的振幅存在显著差异，不过这两个方向的频谱形状大致相同。

设计响应谱

很少有人分析单一时间信号的响应谱，这是因为使用原始信号作为输入对结构执行直接时域分析更为优越。从上面的 El Centro 示例可以看出，某次地震可能会产生在特定频率下具有明显峰值的响应谱。然而，另一次相似地震的峰值则可能发生在其他频率。

为了能够使用响应谱来分析尚未发生的事件，我们创建了设计响应谱，这可以看作是某一地理区域内所有已知和预计地震的包络。例如，ASCE 7-16 和 Eurocode 8 等建筑规范（参考资料 2-3）中提供了这种频谱。设计响应谱中的加速度级通常取决于地理位置和土壤类型。

设计响应谱是响应谱分析的实际输入。

设计响应谱通常根据周期（而不是频率）提供。由于它们彼此互为倒数，因此，在以对数尺度绘图时，这两个图正好形成镜像。

楼层响应谱

典型的地震设计响应谱提供了地面运动对建筑物等主结构产生影响的相关信息。然而，如果我们有兴趣分析安装在建筑物内部的辅助组件或系统，原始响应谱可以提供适当的描述。举例来说，辅助系统可以是管道系统或压力容器，它们将在主结构内其所在的位置受到基座加速度作用。一般来说，这个加速度与地面加速度不同。

楼层响应谱是针对主结构中的特定位置开发的一种设计响应谱。主结构将通过其固有频率充当原始信号的带通滤波器。因此，楼层响应谱通常具有与主结构的固有频率相关的显著峰值。楼层响应谱一词源于这样的事实：这种局部响应谱在建筑物的不同楼层之间往往并不相同。

管道系统等大型系统在其所有支撑点上的楼层响应谱可能都不相同，从而导致分析变得非常复杂。

基于响应谱的分析

多自由度系统

假设一个结构的数学模型通过有限元法进行离散化，得到矩阵形式的运动方程

该结构位于多个点上，这些点连接到具有基本运动的公共“地面”。该矢量的大小与（自由度总数）相同，但它只包含三个不同的值：所有x向平动自由度的、所有y向平动自由度的以及所有z向平动自由度的。此时的相对位移为。在没有外部载荷的情况下，运动方程为

或

这里利用了刚体运动不会在系统中引入任何弹性力或黏性力这一事实，从而得到。

通过在支撑节点固定的情况下求解无阻尼特征值问题，可以计算N阶特征模态集

由于在特征频率分析中，所有特征模态在支撑点处的位移都为零，因此这些特征模态可以表示相对位移（但不能表示绝对位移）。

通过标准的模态叠加运算，可以得到解耦模态方程

假设使用特征模态的质量矩阵归一化，并且阻尼矩阵可以通过特征模态实现对角化。质量矩阵归一化不是必需的，但它可以简化某些表达式。

在上式中，为模态j的模态系数，因此相对位移可以写为特征模态的线性组合，由模态坐标加权：

支撑运动可以沿三个正交方向分解为

矢量对于所有X向平动自由度来说，值都为“1”，对于所有其他自由度则为“0”。由此可得模态运动方程

乘数为模态参与因子；

因此，在响应谱描述的方向k通过基本运动施加载荷时，模态j的最大幅值为

或使用伪加速度谱得到

综上所述，某一特征模态的峰值振幅是相应固有频率（与结构无关）下的响应谱值与参与因子（结构属性，但与载荷无关）的乘积。

模态求和

在实际应用中，多个模态的固有频率都在设计响应谱覆盖的频率范围内，这意味着需要一些响应组合。这种组合的排列需要遵循一些规则，下文将详细说明。

这些求和规则是非线性的。对于任何组合类型，所有结果量都需要严格为正。因此，任何物理量都必须根据其自身的模态响应进行求和。例如，应力分量必须用模态应力计算，而不能从总应变中恢复，且应变也不能从总位移中恢复。这会对响应谱分析结果的解释产生诸多影响。比如：

• 由于各个位移分量不匹配，绘制位移形状没有意义。
• 无法根据单个应力分量计算等效应力（如 von Mises）。
• 如果有交互规则（例如梁中法向力和力矩的组合），则求和方式比较敏感。守恒解释可以分别确定这两个物理量，然后计算总和与差。
• 如果您要将响应谱分析结果添加到静载荷工况（如静载）下的结果中，必须特别注意各种符号。

我们一般在三个正交方向提供激励。一般的方法是分别考虑这三个方向的激励。首先，对每个方向的所有模态响应求和，然后对三个方向的结果求和。下文描述的 CQC3 求和规则属于例外情况，其中空间和模态求和是同时进行的。

周期模态和刚体模态

通常，将特征模态分为周期模态和刚体模态会非常有用。这种区分与激励相对于模态特征频率的频率含量有关。

在上述响应谱中，可以识别出以下特征域：

区域	描述	响应类型
A-B	放大的周期谱位移	周期性
B-C	放大的周期谱速度	周期性
C-D	放大的周期谱加速度	周期性
D-E	从放大的周期谱加速度到刚性谱加速度的过渡	周期性与刚性混合
E-F	从刚性谱加速度到最大基座加速度的过渡	周期性
F-G	最大基座加速度	周期性

上表基于 NRC RG 1.92参考资料 1。

在高频模式下，振子的质量主要在与支架同相的情况下进行转换，这种模态构成刚体模态，它们的响应相互同步（并与基本运动同步）。这意味着，对刚体模态来说，应使用纯求和（包含符号）进行计算。

具有显著动态响应的模态构成周期模态。由于这种模态的周期不同，其最大值在时间上不同程度地呈随机分布。因此，响应的周期性部分需要使用更复杂的求和技术。一般来说，最大值的简单相加会大大高估真实响应。

处于过渡区域的模态一部分构成周期模态，另一部分构成刚体模态。另外，有时还需要添加一些包含丢失质量修正的静载荷工况。

在下面的表达式中，表示由方向的激励引起的任意结果物理量。例如，可以是位移、速度、加速度、应变分量、应力分量、有效应力或梁截面力。的周期性部分表示为，刚性部分表示为。同理，和分别表示针对特征模态j的计算结果。

并非所有分析都需要分为周期模态和刚体模态，如果不加以区分，则所有模态均视为周期模态。

模态划分：周期模态和刚体模态

我们通常可以使用两种不同的方法进行模态划分。不论使用哪种方法，对于模态j来说，

由此可得

这两种方法的区别在于如何确定系数。在低频情况下，该系数接近 0，在高频情况下，则接近 1。

Gupta 方法

在 Gupta 方法中，是固有频率对数的线性函数。

这里的和是两个关键频率。据此可以确定，特征频率低于时，对应的模态被视为纯周期模态，高于时，对应的模态被视为纯刚体模态。在原始的 Gupta 方法中，较低的关键频率由下式给出

其中，和分别是加速度谱和速度谱的最大值。在上述理想化频谱中，最大值出现在D点位置。

对于第二个关键频率，应仔细加以选择，确保高于该频率的模态表现为刚体模态。该频率可以取为不同阻尼比的响应谱相互收敛时的频率。

Lindley-Yow 方法

在 Lindley-Yow 方法中，系数直接取决于响应谱值，而不仅仅取决于频率。因此，我们可以认为特定的模态在不同的激励方向表现出不同程度的刚性。

零周期加速度（ZPA）是事件持续期间的最大地面加速度，

这也是响应谱中绝对加速度（或伪加速度）的高频渐近值，它对应于理想频谱的 F-G 部分。

由此得到，

出于物理原因，的值必须在 0 到 1 范围内，并随频率增加。因此，NRC RG 1.92（参考资料 1）要求，对于 C 点以下的任何特征模态，都必须设为零。

对周期模态和刚体模态求和

分别对所有模态的周期响应和刚性响应求和后，可以将其组合为

对周期模态求和

绝对值相加法

最保守的方法是对所有N阶模态的最大响应求和，因此假设所有模态同时达到最大值。在许多情况下，采用这种方法会导致设计过于保守。

在最坏的情况下，使用N阶非紧密间隔模态得到的预测结果可能比使用以下其他方法得到的结果大倍。

完全二次组合法

最常用的周期模态叠加方法是完全二次组合（CQC）法：

模态之间的相互作用由模态相互作用系数（）确定。由于对称，并且当时，因此使用以下等价表达式可以提高计算效率

实际上，上述表达式对多个计算规则有效，唯一的区别是如何计算。下面给出了多个这样的表达式。当一种方法被认为是完全二次组合法时，通常意味着需要使用 Der Kiureghian 相关系数。

Der Kiureghian 相关系数

模态相互作用系数定义如下

其中，和是两个模态的固有频率，和是对应的模态阻尼比。

对于常见的均匀阻尼情况，该表达式可以简化为

两种不同模态和的响应可能包含不同的符号，因此交叉项对总和的贡献可能为负。这是故意为之，但人们普遍误解为应该使用和的绝对值。然而，基础分析基于一个假设，即响应是振型的线性函数。如果不是这种情况，则使用绝对值是一种更安全的方法。最常见的非线性结果量（比如有效应力）总为正值，在这种情况下，总和中的所有项都会给出正的贡献。

两种模态之间相关性的强弱取决于模态频率比，但很大程度上也取决于阻尼。

二重和法

二重和法采用模态相互作用系数。该系数称为 Rosenblueth 相关系数，在概念上类似于 Der Kiureghian 相关系数。

二重和法有两种变体：

（NRC Regulatory Guide 1.92, rev 1）


（NRC Regulatory Guide 1.92, rev 2, 3）

这种方法的旧版本实际上存在错误，但结果比新版本更保守，因此使用旧版方法没有任何风险。

在任一版本中，

其中

且

这里，是单独的输入项。动态事件的持续时间和是模态阻尼比。当的值较大时，二重和法中的模态相关因子与 Der Kiureghian 模型的相似。当的值较小时，二重和法预测的相关性要强得多。

SRSS 法

SRSS 法不包含模态之间的任何相互作用；也就是说，

这种方法仅适用于模态间隔不紧密的情况；即，任意两个特征频率都不相互接近。所有其他方法都以不同方式包含了模态之间可能存在的相互作用。

分组法

模态按照以下规则进行分组：

1. 通过添加最低阶（频率）、尚未分组的特征模态k来创建新组m
2. 从k开始逐步提高特征频率
3. 只要满足，便将模态i添加到组中
4. 回到步骤 1

使用列表中的所有特征模态后，会得到许多组，其中一些组可能只包含一个特征模态。两个模态之间相关因子的规则为

这里使用的sign()运算符是一种表示模态响应乘积绝对值加到总和中的方式，这是因为

百分之十法

固有频率差小于 10% 的特征模态会得到特殊的交互处理，从这个意义上来说，百分之十法类似于分组法。模态相关系数为

从上式可以看出，如果任意一对特征频率的差都大于 10%，则分组法和百分之十法都等同于 SRSS 法。然而，当使用 CQC 法时，除非阻尼非常小，否则这些模态也被视为在较大间距下显著耦合。

刚体模态求和

在对刚体模态求和时，我们可以使用两种组合方法。

组合方法 A

刚体模态通过下式求和

其中，是在求解丢失质量时，对静载荷工况的求解结果，如下文所述。

组合方法 B

仅当Lindley-Yow 方法与静态 ZPA 方法结合使用时，才能使用这种组合方法。此时的刚体模态响应非常简单

丢失质量修正

丢失质量法

由于模态叠加使用的模态数有限，因此分析中常会丢失一些质量（归因于未使用的模态）。在假设高阶模态没有任何动态放大的前提下，可以通过求解一些额外的静载荷工况来设计修正，这些工况包含作用于“缺失”质量的峰值加速度。在评估支撑力时，静校正的效果往往最为显著。

实际上，静校正常常可用于模态叠加。不过，在进行响应谱分析时，需要简化表达式。

静校正载荷矢量通常可以计算为：

其中，为原始载荷矢量，为模态载荷；这是物理载荷在每个特征模态上的投影，

在基座激励情况下，与I方向激励相关的载荷矢量为

从而得到模态载荷

进一步得到，

刚体模态的峰值加速度等于零周期加速度（ZPA）。这是事件持续时间内的最大地面加速度，

这也对应于加速度谱的高频渐近值。

因此静载荷为

现在，通过求解标准静态问题，可以为丢失质量提供额外的位移校正方法

其中，表示刚度矩阵。

以下表达式

可以看作是一种辅助模态。在这种情况下，它是一个长度为自由度数的矢量。

静态 ZPA 方法

使用这种方法时，我们不需要推导丢失质量。此方法只能与 Lindley-Yow 方法一起用于分离周期模态和刚体模态。根据此方法，所有刚体模态都具有加速度，这个加速度会施加给整个结构。因此，静载荷工况只是纯重力载荷，但按（而不是重力加速度）进行缩放。

在空间方向求和

一般情况下，应用设计响应谱的三个正交方向不能随意进行选择。结构在特定的方向可能更容易被激励。

就地震而言，我们通常假设三个正交方向的激励在统计意义上相互独立。在大多数情况下，我们没有理由假设两个水平方向的激励具有不同的频谱特性。因此，通常在两个水平方向使用一个设计响应谱，在第三个垂直（Z）方向使用另一个设计响应谱。

不过，即使两个水平方向的激励具有相同的频谱特性，通常也可以合理地假设二者具有不同的幅值。此时可以认为局部Y方向的频谱是局部X方向频谱的缩放版本，

X方向不是地理位置的属性，但您可以选择这个方向来分析最坏的情况。然而，对于所有结果物理量或结构中的不同位置，引起最高响应的加载方向可能不同。某些结构有一个明显的“弱”方向，您可以选择此方向作为“X”方向。但更多时候，情况并非如此。因此有三种可以采用的方法：

• 在两个水平方向使用相同的频谱；即。这种方法比较保守。
• 运行多次单独的分析，其中将X方向旋转到不同的方向。如果 15 度的旋转增量已经足够小，则需要执行七次分析。
• 使用组合规则（CQC3），其中涵盖了所有可能的旋转。

下面介绍几种不同的空间组合方法。

SRSS 法

在平方和的平方根（SRSS）方法中，总和通过下式计算

该表达式基于一个假设，即三个方向的峰值响应之间具有统计独立性。如果在两个水平方向使用相同的频谱，使用这种方法就足够了。

100-40-40 方法（百分比法）

在这种方法中，来自最弱方向的贡献取全值，而另外两个贡献则有所减少。常用的变体有两种：40%（100-40-40）方法和 30%（100-30-30）方法。解释很明确：在最弱方向达到峰值时，其他方向的值不高于各自峰值的 40%（30%）。

将三个方向的响应重新排序，得到

此时，40% 方法的总响应可通过下式计算

在这个规则的某些公式中，不采用重新编号，而是将表达式写为

实际上，只要在对多个响应结果求和时适当考虑这些符号，就能得到相同的结果。

与 SRSS 求和相比，40% 方法更为保守。对于某些值的组合来说，30% 方法则明显是非保守的。

百分比法不是空间各向同性的。就对称结构而言，由于其对称性，应具有相同载荷水平的构件不会出现这种情况。加速度方向的参考轴方向非常重要。

CQC3 方法

CQC3 方法将 CQC 原则扩展为空间组合，同时执行振型组合和空间组合。这种方法主要适用于仅分析周期模态的情况。

与标准 CQC 方法一样，每个载荷方向的模态响应总和计算如下

其中使用了的 Der Kiureghian 表达式。

此外，还可以形成一个类似的表达式，其中给出两个水平方向的频谱响应之间的交叉耦合：

现在，我们在概念上假设响应谱应用于局部坐标系 X'-Y'，该坐标系绕 X-Y 方向旋转一个角度。如果响应是特征模态的线性函数，则可以得到

另外，如果所应用频谱的关系为，则会对响应也应用相同的比例。作为旋转角度函数的峰值响应可通过 SRSS 求和方法得到

从上式可以看出，当时，可以恢复为标准 SRSS 表达式。

角可以给出最大响应，与无关，它的值为

有两个根，您必须检查这两个根才能确定最坏的情况。

CQC3 方法的亮点在于，同一频谱可以应用于任意一对正交轴，其中考虑了二次频谱的比例以及最弱方向的定向问题。

然而，请注意，如果研究非线性响应量，则 CQC3 方法并不精确。在这种情况下，基本正确的唯一选择是沿多个旋转轴实际应用频谱。

SRSS3 方法

SRSS3 方法是 CQC3 规则的特例，其中忽略了模态相关性；即

这种方法保留了通过搜索来选择最弱方向的属性。

发布日期：2019 年 1 月 28 日
上次修改日期：2019 年 1 月 28 日