学习中心

Copying and Reusing Boundary Mode Analysis Results

---

When using theBeam Envelopesor theElectromagnetic Waves, Frequency Domaininterfaces in COMSOL Multiphysics^®, one can often have multiplePortboundary conditions that have identical structures but are at different locations in space. It is often the case, especially for optical and photonics models, that multiple different modes at these ports are of interest, and these modes need to be numerically computed. It is possible to compute all of the modes of interest using just a singlePortboundary condition of typeNumericand to copy and reuse these solutions in all of the other ports in the model, which will beUser-Defined Ports.

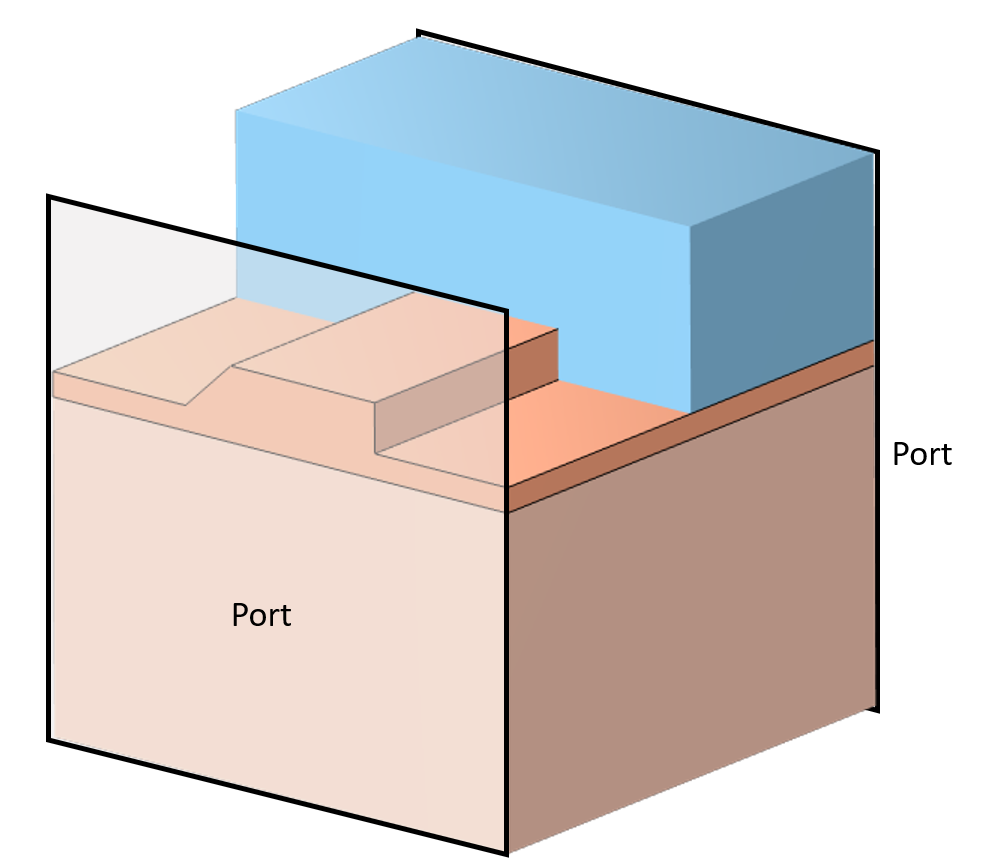
A supporting example is shown below: an optical ridge waveguide that does not change shape along the length. A mode of a particular polarization is launched, but other modes can exist due to anisotropic properties that exist in part of the substrate. For this example, the first two modes of propagation are considered.

A uniform waveguide with two ports that support multiple modes.

Precomputing All of the Modes of the Waveguide

This technique begins with first defining aNumeric Portthat will be used to compute all of the modes of interest. Since thePortwill not be used directly in the ultimate analysis, give it aPortnumber of 0 to clearly differentiate it. Apply thePortboundary condition to the boundaries describing the waveguide. For optical waveguides, ensure that the width of the cladding region is large enough that the fields fall off to nearly zero.

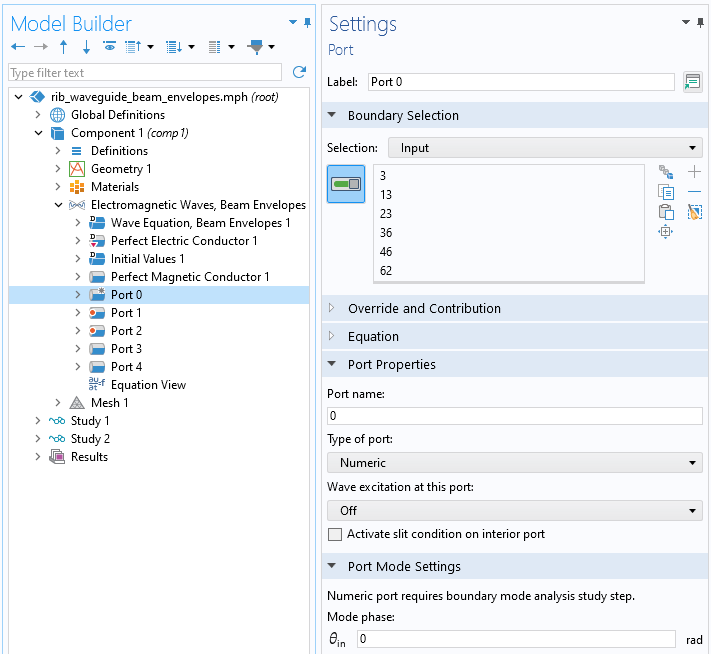
Setting up a singleNumeric Port.

Set up a study containing a boundary mode analysis that solves the modes of thisPort. In this example, only the first two modes are of interest, so set theDesired number of modesto 2, and set theSearch for modes around shiftsetting to an effective mode index of 3.5, which is the highest refractive index in the waveguiding structure. This will compute the first two modes supported by this waveguiding structure at this frequency.

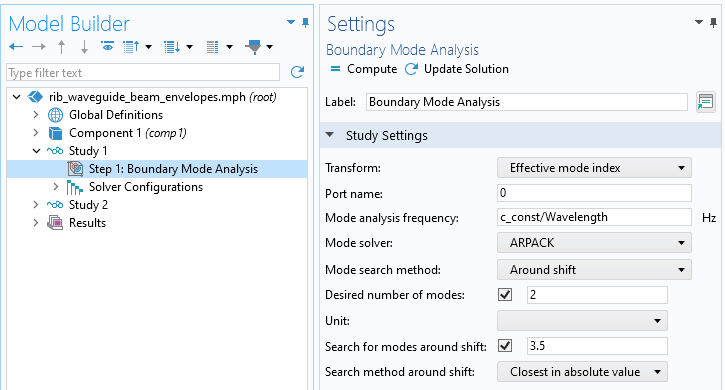
Solver settings for computing all of the modes of interest.

Once the study is solved, it is helpful to create plots of the boundary mode electric field to verify the computed modes. It is these fields that will be used in the next step to define a set of user-defined ports.

Visualization of the two modes of interest.

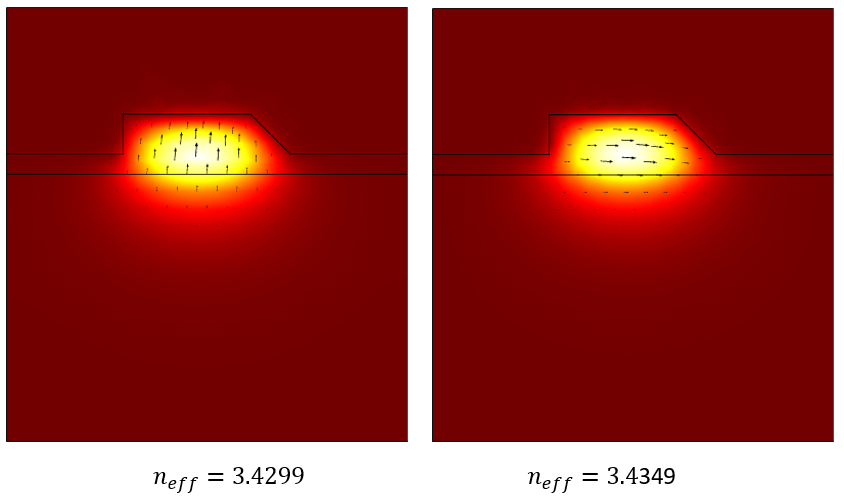
Understanding and Using the Outputs of the Boundary Mode Analysis

The total boundary mode electric field is composed of two orthogonal components, the electric field tangent to the boundary and the electric field normal to the boundary. The total electric field is:

,

where the tangent component of the field is a vector that lies in the plane of the boundary, and the normal component is a scalar field. The normal vector,, is the vector pointing outward from the modeling domain; it points in the direction of an outgoing signal.

For port index 0, the components of the tangential field are:ewbe.tEbm0x,ewbe.tEbm0y, andewbe.tEbm0z, and the normal component isewbe.nebm0. The components of the outward normal vector areewbe.nx,ewbe.ny, andewbe.nz, and so the total electric field of the mode on that boundary is:

ewbe.tEbm0x-ewbe.nx*ewbe.nebm0

ewbe.tEbm0y-ewbe.ny*ewbe.nebm0

ewbe.tEbm0z-ewbe.nz*ewbe.nebm0

Each of the two computed modes ofPort 0will have a different tangential and normal component, as well as a propagation constant:ewbe.beta_0. To refer to these variables, use thewithsoloperator, which has the following syntax:withsol('sol1',Ex_total, setind(lambda,M1)).

The first argument is the solution tag, so any solution can be referred to. (See also:Examples of the withsol Operator.) The second argument is the expression to evaluate from that solution, and the third argument uses thesetindoperator, which here uses one of two parameters,M1=1,M2=2, to refer to the two modes computed by theBoundary Mode Analysisstudy. This operator allows for the reuse of these precomputed solutions.

Next, the fields computed onPort 0have to be mapped to the other boundaries where they will be needed. This is done via theGeneral Extrusionoperator with settings as shown in the screenshot below. The input and output ports are at identicalxy-coordinates, so no change to the mapping of these is needed. Thez-expression ofz-Lengthis used here because the output boundaries are offset in thezdirection by theGlobal Parameter,Length. This operator will make the data computed on the input boundaries available on the output boundaries. For full details on using theGeneral Extrusionoperator, including for rotating the fields, see:Examples of the General Extrusion Operator.

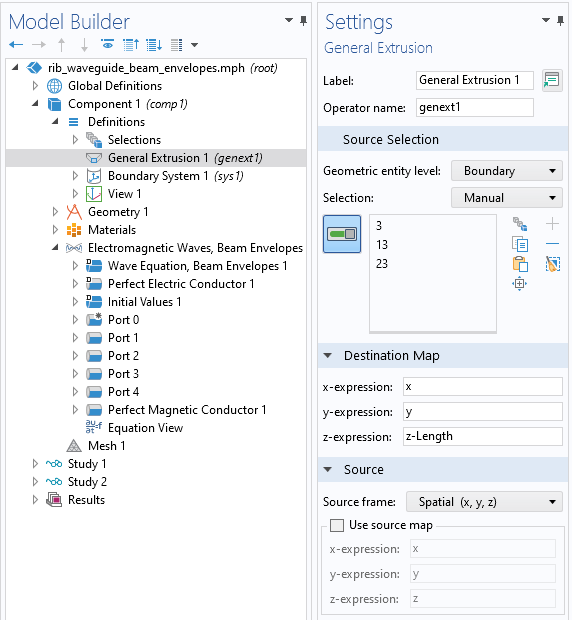
The settings for theGeneral Extrusionoperator, which maps data from one boundary to another. Note theVariablesnodes underDefinitions_, where the_ withsolandGeneral Extrusionoperators are used to define the mode fields and propagation constants forPort 1toPort 4.

To use this operator, which has the default namegenext1, at the other port boundaries, wrap the previously developed expressions with thegenext1()operator. So, for example, the total electric field of the first mode, mapped to the outgoing port, is of the form:

genext1(withsol('sol1',ewbe.tEbm0x,setind(lambda,M1)))-ewbe.nx*genext1(withsol('sol1',ewbe.nebm0,setind(lambda,M1)))

genext1(withsol('sol1',ewbe.tEbm0y,setind(lambda,M1)))-ewbe.ny*genext1(withsol('sol1',ewbe.nebm0,setind(lambda,M1)))

genext1(withsol('sol1',ewbe.tEbm0z,setind(lambda,M1)))-ewbe.nz*genext1(withsol('sol1',ewbe.nebm0,setind(lambda,M1)))

Note that theGeneral Extrusionoperator is not applied to the components of the normal vector since this has different components on opposite boundaries. In practice, a set of variables can be created to simplify this syntax.

Using the Precomputed Modes and Setting up the Model

To define the waveguide model where allPortsare using these precomputed mode fields, begin by defining the excitation port,Port 1, on the same set of boundaries wherePort 0was defined. Set theType of porttoUser definedand, within thePort Mode Settingssection, use the previously defined variables that refer to the total electric field and propagation constant at each of the four ports.

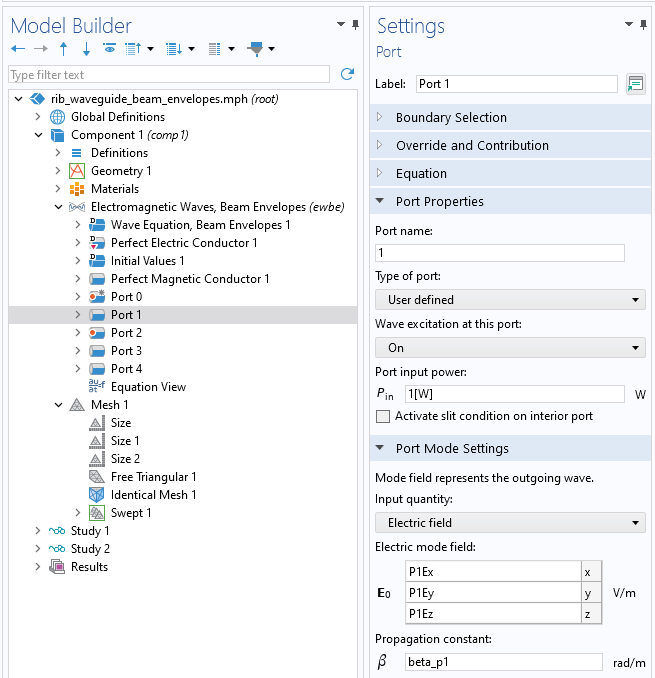
Settings for a port to reuse previously computed electric fields and propagation constants that exist at the same boundaries.

Repeat the abovementioned steps and definePort 2on the same set of boundaries. This is an unexcited port that will monitor reflections back into the second mode. Set the wave excitation off, and use the variablesP2Ex,P2Ey, andP2EzforElectric mode fieldandbeta_p2forPropagation constant. Also define two more ports for the outgoing signal on the far side.

It is a requirement that the meshes on allPortboundaries are identical, and this condition can be satisfied in general via theIdentical Meshfeature, as shown in the screenshot below.

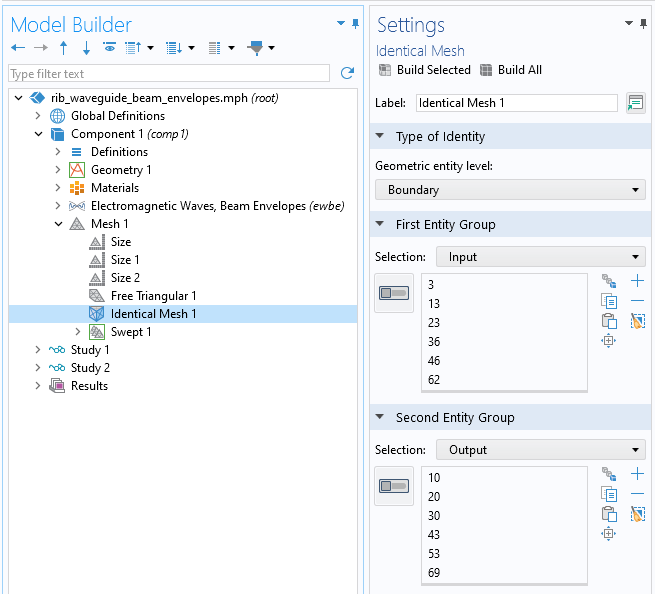
Using theIdentical Meshfeature to ensure that the mesh on the input and output ports are identical.

In regard to meshing for this particular case, the mesh must be sufficiently refined both in the cross-sectional plane and along the length. Since the supported modes in the anisotropic substrate region are slightly different from the isotropic substrate region, the mesh refinement along the length must be studied. For further guidance on meshing and solving such models, see theDirectional Couplermodel.

When solving, an optionalStudy Referencecan be used to recompute thePort 0modes before solving the 3D model. In theWavelength Domainstudy step, disablePort 0within thePhysics and Variables Selectionsection, as shown below.

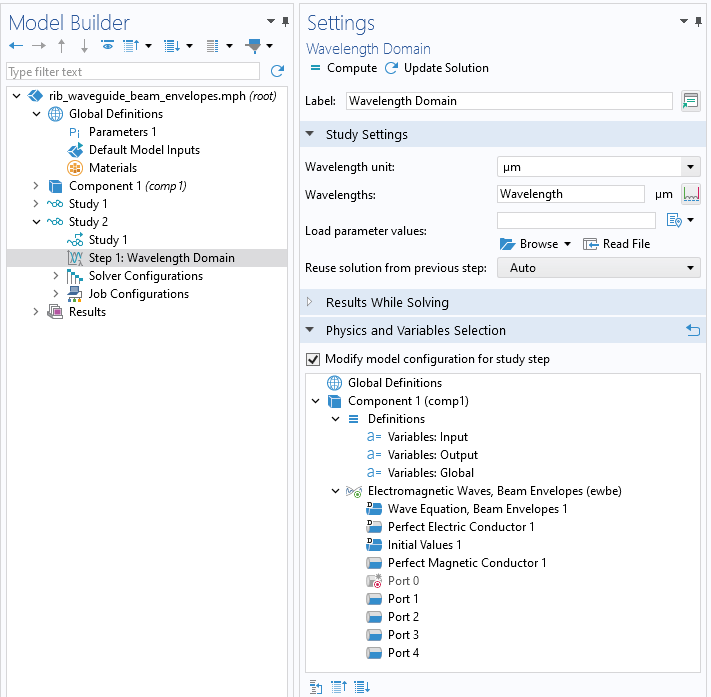
Visible in theSettingswindow,Port 0is disabled when computing the fields within the model.