学习中心

Course:

Modeling with Partial Differential Equations in COMSOL Multiphysics

Modeling with PDEs: Multiphysics Systems of Equations

In Part 8 of this course on modeling with partial differential equations (PDEs), we will learn how to use the PDE interfaces to model systems of equations. As an example, we will use theCoefficient Form PDEinterface to recreate the built-in functionality available in theJoule Heatingmultiphysics interface, available from the Model Wizard. Using the predefined multiphysics interface for Joule heating is, of course, much easier and quicker for this type of modeling compared to implementing this by hand. However, learning how to set up the corresponding equation system from scratch will prepare you for setting up more general systems, including systems that are not available as a built-in option in the COMSOL Multiphysics^®software.

Modeling with Multiple Dependent Variables

All PDE interfaces and equation forms support the use of multiple dependent variables in a system of PDEs, which can be coupled in several different ways. For a complete description of what options are available for modeling systems of equations, see theCOMSOL Multiphysics Reference Manualdocumentation, specifically theMultiple Dependent Variables — Equation Systemssection of the chapter,Equation-Based Modeling.

There are several different types of equation systems that can be modeled using the equation-based, orMathematics, interfaces. For example:

When the variables represent different physics. One example of this is Joule heating where the dependent variables are the voltage,, and the temperature,.
When the variables represent the same physics. In such cases, the dependent variables frequently represent the components of a vector or tensor field, such as the displacement field components for structural mechanics.
Combinations of 1 and 2.

In this article, we will look more closely at the case of Joule heating, a system of type 1, as mentioned here. In thenext articlewe will study systems of type 2.

Joule Heating and Variables that Represent Different Physics

When the equation system represents Joule heating, the system of PDEs can be written as:

whereis the electric conductivity,is the density,is the heat capacity, andis the thermal conductivity. The first equation is that of conservation of currents. The second equation is the heat transfer equation with a Joule heating source term.

Note that the Joule heating source term can also be written as:

There are multiple ways of defining a Joule heating system of equations in COMSOL Multiphysics^®. To learn more about using the built-in options, see our Learning Center course ondefining multiphysics models.

As an alternative to using the built-in physics interfaces, you could instead define this system of equations using theCoefficient Form PDEinterface,General Form PDEinterface, orWeak Form PDEinterface. Here, we will focus on using theCoefficient Form PDEinterface. For this, we can use what we learned in the Learning Center article onmodeling with PDEs for diffusion-type equations.

We can identify the first equation as Poisson's equation. This means that for the stationary version ofCoefficient Form PDE:

we can identify the coefficients as:

and all other coefficients are zero. For the heat equation

we need to compare with the transient version ofCoefficient Form PDE:

we see that:

UsingCoefficient Form PDE, there are two ways of entering this equation system: as a system of two scalarCoefficient Form PDEinterfaces or as a system of one vector-valuedCoefficient Form PDEinterface with two vector components,and.

Joule Heating as a System of Two Scalar Coefficient Form PDE Interfaces

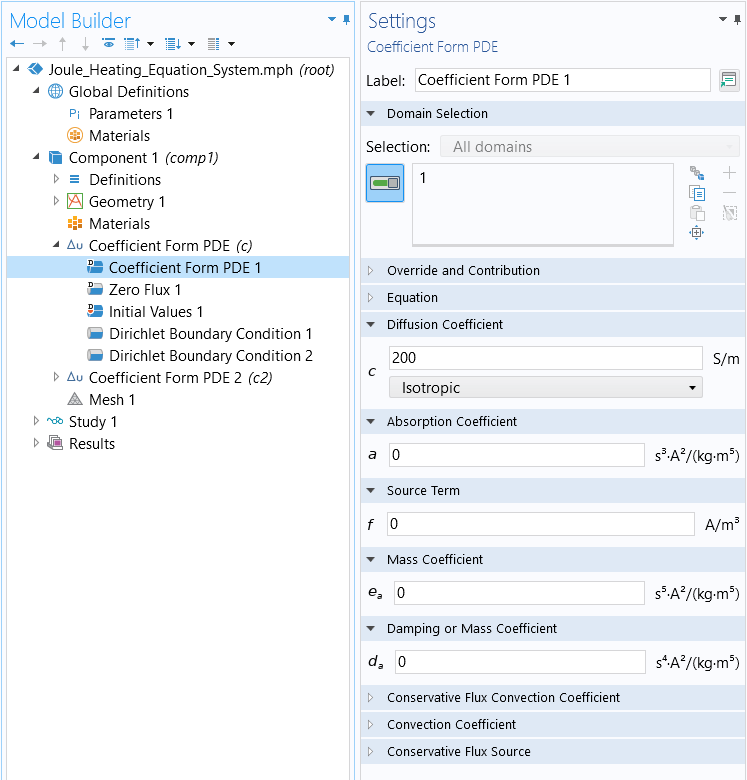
Using two scalarCoefficient Form PDEinterfaces is very similar to using predefined physics interfaces. Start by adding aCoefficient Form PDEinterface, where we have changedField nameandDependent variablestoV.

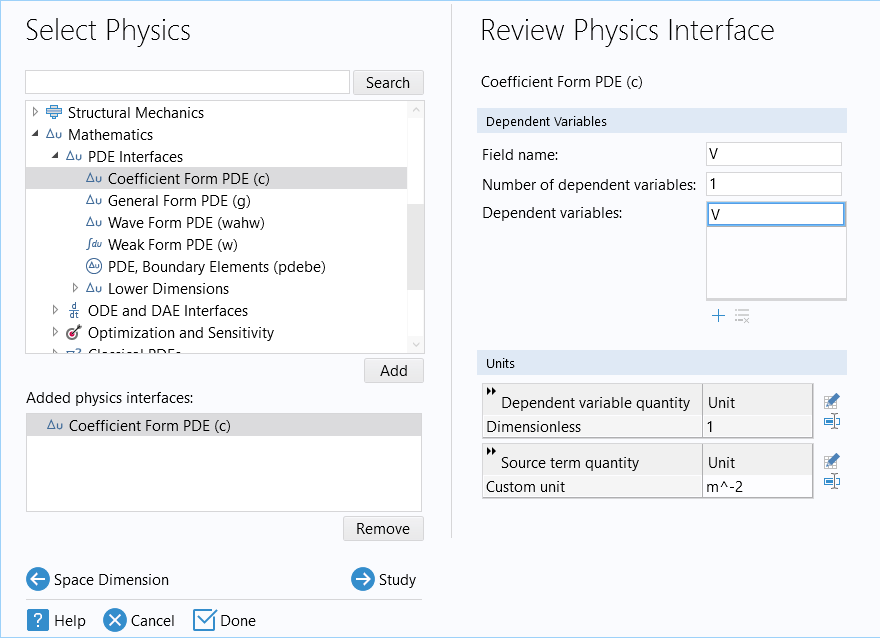
The Select Physics window with Coefficient Form PDE selected and the corresponding Review Physics Interface window.
TheSelect Physicswindow, where theCoefficient Form PDEinterface has been added to the model.

Next, add anotherCoefficient Form PDEinterface with bothField nameandDependent variablesset toT.

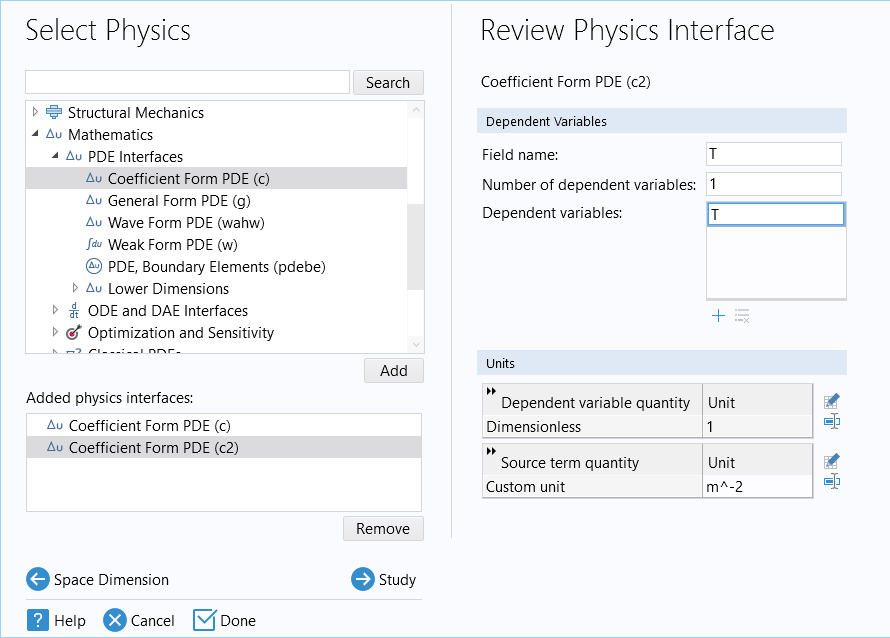
The Select Physics window showing that a second Coefficient Form PDE has been added and the corresponding Review Physics Interface window.
A secondCoefficient Form PDEinterface added through the Model Wizard.

In this case, there is no reason to have different names forField nameandDependent variables. However, if we create a vector-valued system of equations, then we can useField nameas a reference for a vector of dependent variables.

In the next step, select aTime-Dependentstudy. The Model Builder tree appears as follows:

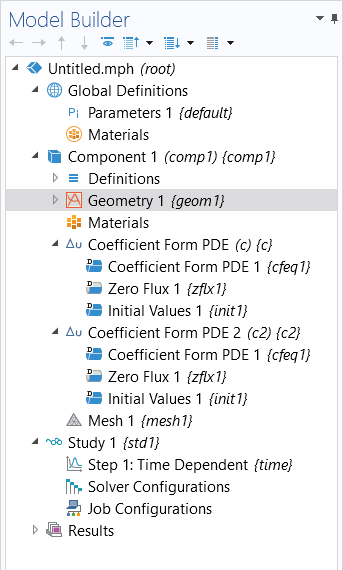
The Model Builder window with Geometry 1 selected.
The model tree after adding the physics interfaces and study through the Model Wizard.

For this example, we will use a simple conductive block that is 1-by-0.1-by-0.01 mm, having a boundary condition of 1 V on one side and 0 V (or ground) on the other side.

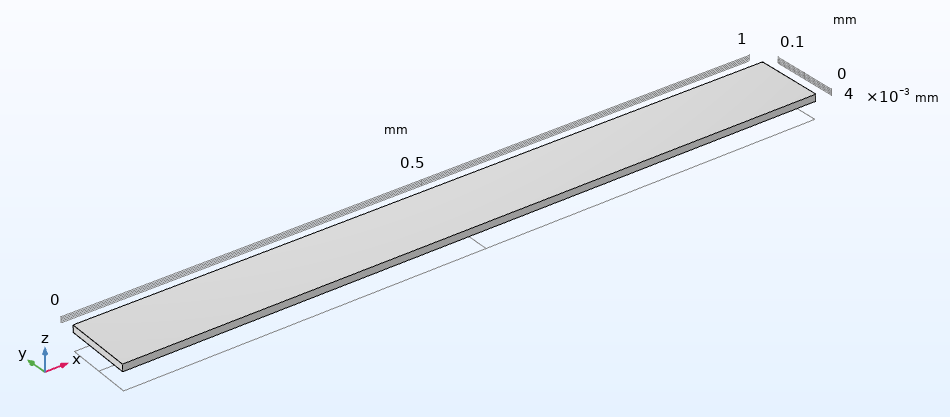
A model of a conductive block with its measurements labeled in mm.
The model geometry for a simple conductive block.

Choosing Units

In theSettingswindow for theCoefficient Form PDEinterface, change the units for theDependent variable quantitytoElectric potential (V)and theSource term quantitytoCurrent source (A/m^3).

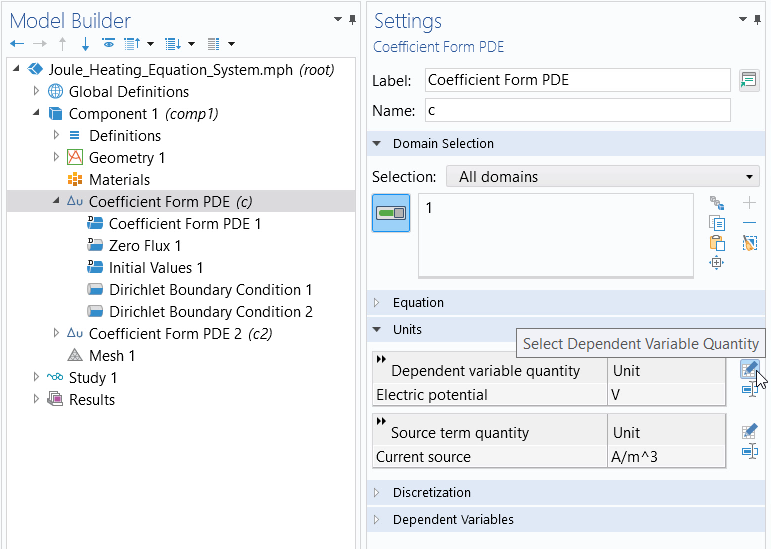
The Model Builder with the Coefficient Form PDE interface selected and the corresponding Settings window.
The settings for the firstCoefficient Form PDEinterface.

You can do this by clicking the respective icon (pictured below) that opens thePhysical Quantitydialog box. From there, you can select the appropriate quantities.

The Physical Quantity box with Electric potential (V) highlighted.

The Physical Quantity box with Current source (A/m^3) highlighted.

The Physical Quantity box with Dimensionless (1) highlighted.

ThePhysical Quantity dialog box, with the different selections for the physical quantities displayed (left, center) as well as where to choose a dimensionless quantity (right).

If you do not want to work with units, you can select theDimensionlessoption in theGeneralsection of thePhysical Quantitydialog box.

Conservation of Currents

If we assume an electric conductivity, corresponding to a moderately conductive material, then theCoefficient Form PDEnode settings are as follows:

The Model Builder with the Coefficient Form PDE node selected and the Coefficient Form PDE settings.
The settings for theCoefficient Form PDEnode.

Using aDirichlet Boundary Condition, set the voltage to 1 V on the left boundary. Similarly, we can add a secondDirichlet Boundary Conditionfor the boundary on the right end with the voltage equal to 0 V, corresponding to ground.

The Model Builder with the Dirichlet Boundary Condition selected, the corresponding Settings window, and the Graphics window with the conductive block model.
The settings for theDirichlet Boundary Condition.

Heat Transfer

In theSettingswindow for the second interface,Coefficient Form PDE 2, change the units toTemperature (K)for theDependent variable quantityandHeat source (W/m^3)for theSource term quantity.

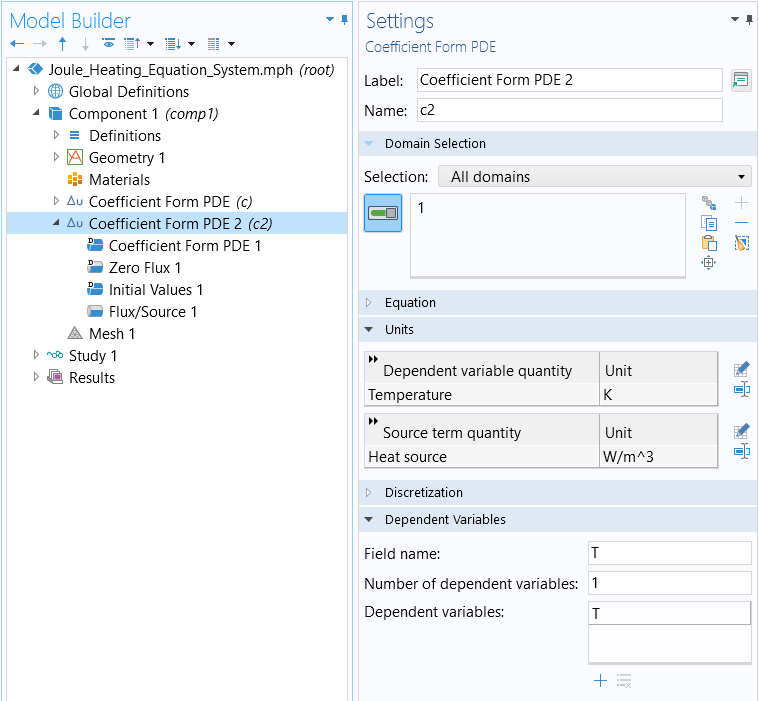
The Model Builder with the second Coefficient Form PDE interface selected and the corresponding Settings window.
The settings for the secondCoefficient Form PDEinterface.

Using the electric conductivityand further assumingand, theCoefficient Form PDEnode settings for the second equation are as follows:

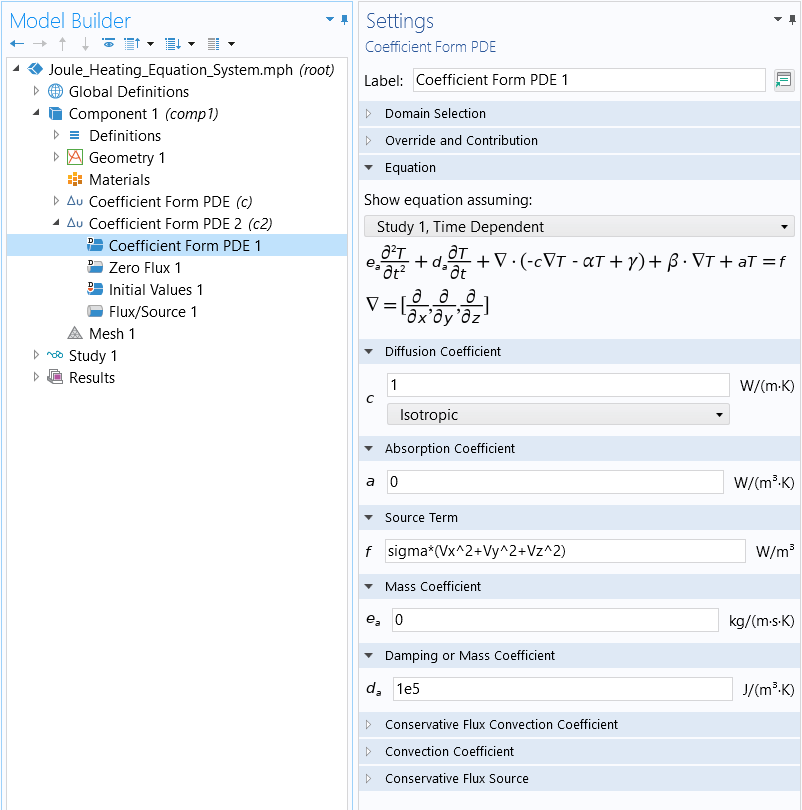
The Model Builder with the Coefficient Form PDE node for the second Coefficient Form PDE interface selected and the corresponding Settings window.
The settings for theCoefficient Form PDEnode for the second equation.

where the source term corresponds to

In the software, the derivative components of a dependent variable, up to derivatives of the second order, are always available as expressions for dependent variable names, with the spatial components appended. If the dependent variable isV, then the derivative components are available asVx,Vy,Vz,Vxx,Vxy, and so on.

For the second equation, for all boundaries, use aFlux/Sourceboundary condition:

with the coefficientand. This boundary condition means that the boundaries are being cooled at a rate that is proportional to the temperature difference of the surroundings. Note that this boundary condition can equivalently be implemented by settingand.

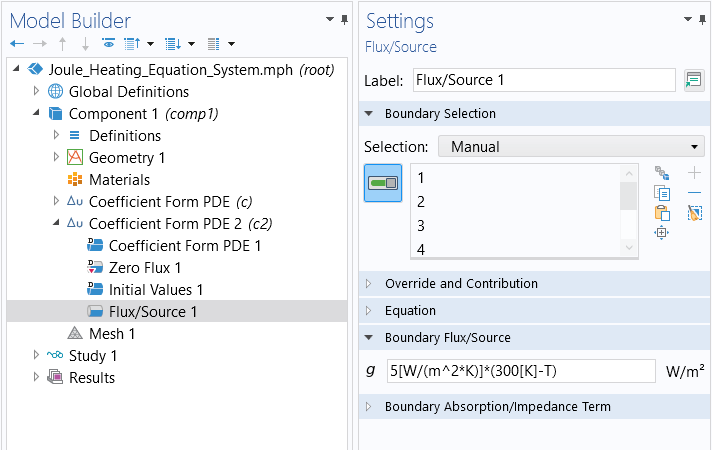
The Model Builder with Flux/Source 1 selected and the Flux/Source settings.
The settings for theFlux/Sourceboundary condition.

The second equation has a time-derivative term and therefore requires updating the values for theInitial Valuesnode. We will assume that the device is at 300 K at time t = 0. Since this PDE only has a first-order time derivative, we do not need to worry about the initial condition for $\frac{\partial{V}}{\partial{t}}, which is only used if we have second-order time derivatives.$

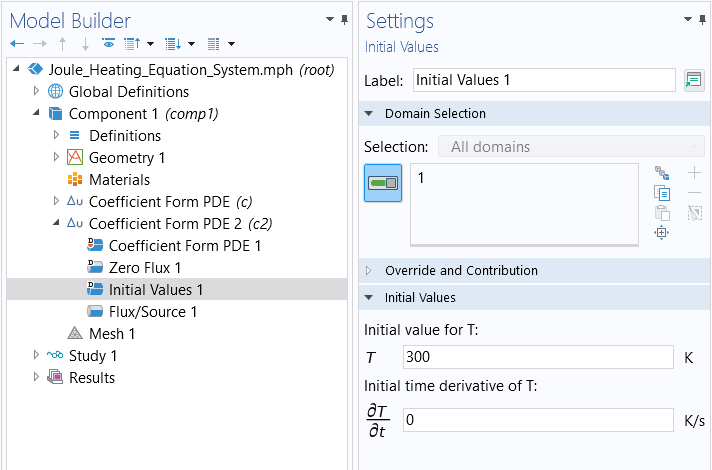
The Model Builder with Initial Values 1 selected and the corresponding Settings window, showing 300 as the initial value for T.
The settings for theInitial Valuesnode.

Results

Now, runStudy 1using the default settings for theOutput timesbetween 0 and 1 seconds with results output for every 0.1 seconds.

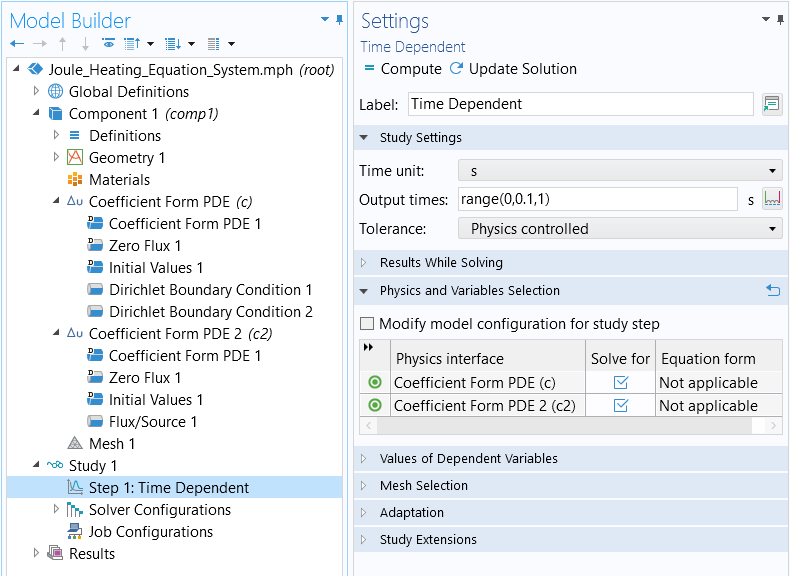
The Model Builder with Step 1: Time Dependent selected and the corresponding Settings window, showing the first and second Coefficient Form PDE interfaces under selections.
The settings for the time dependent study performed.

The result is a temperature of around 480 K at around 1 second.

The conductive block model showing the temperature distribution, with the center being yellow and the ends darkening into purple and black.
Results for the temperature distribution of the block.

We can also plot the voltage drop across the object.

The conductive block model showing the electric potential, with the left end being red, a rainbow ombre in the middle, and the right end being blue.
Results for the electric potential of the block.

You can now define variables for quantities, such as the electric field or current density, and then use them in expressions.

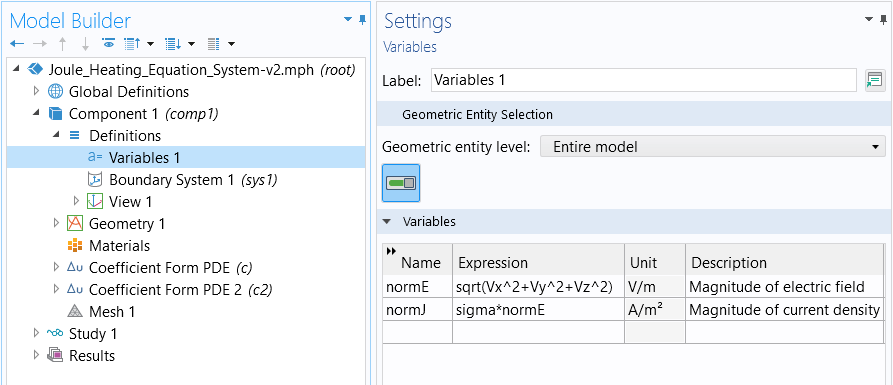
The Model Builder with Variables 1 selected and the corresponding Settings window, where the variable names, expressions, units, and descriptions are visible.
The variables defined after computing the study.

After solving again, we can, for example, visualize the variablenormJin a plot.

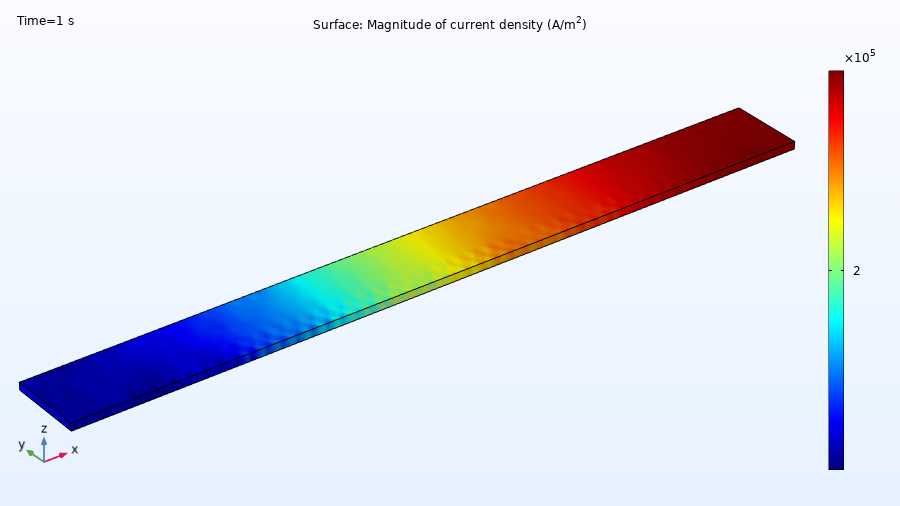
The conductive block model showing the electric potential, with the left end being blue, a rainbow ombre in the middle, and the right end being red, with ripples visible throughout.t
Results for the magnitude of current density of the block.

Further Learning

Although the model used throughout this article is available for download, we encourage you to first build the model yourself by following the guidance provided here. Thereafter, you can open and explore the model file. This will reinforce how to set up equation systems from scratch.

请提交与此页面相关的反馈，或点击此处联系技术支持。